高三期中考试数学试卷
第I卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．若集合
等于 （ ）
A．M B．N C．R D．{（2，4），（－1，1）}
2．若a，b∈R，则使a+b>1成立的一个充分不必要条件是 （ ）
A．a+b≥1 B．a≥
且b≥
C．b<－1 D．a≥1
3．如果直线l将圆
平分，且不经过第四象限，那么l的斜率的取值范围是 （ ）
A．[0，2] B．[0，1] C．[0，] D．[－，0]
4．已知直线a和平面
、
，
、内的射影分别为直线b和c，则b、c的位置关系是 （ ）
A．相交或平行 B．相交或异面 C．平行或异面 D．相交，平行或异面
5．若
，则实数m的值为 （ ）
A．1 B．－1 C．－3 D．1或－3
6．双曲线
的右准线与两条渐近线交于A，B两点，右焦点为F，且FA⊥FB，则双曲线的离心率为 （ ）
A．
B．
C．
D．2
7．已知、都是第二象限角，且
，则 （ ）
A．< B．
C．
D．
8．有一名同学在书写英文单词“error”时，只是记不清字母的顺序，那么他写错这个单词的概率为 （ ）
A．
B．
C．
D．
9．棱长为4的正方体ABCD—A1B1C1D1中，P、Q是CC1上两动点，且PQ=1，则三棱锥P—AQD的体积为 （ ）
A．8 B．
C．3 D．
10．把曲线
按向量
（1，2）平移后得曲线C2，曲线C2有一条准线方程为x=5，则k的值为 （ ）
A．±3 B．±2 C．3 D．－3
11．由1，3，5，…，2n－1，…构成数列
，数列
满足
，则b5等于 （ ）
A．63 B．33 C．17 D．15
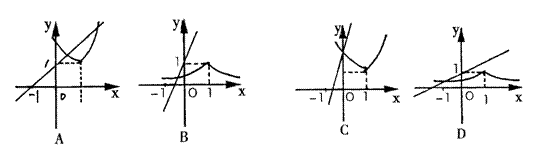
12．已知函数
，在同一直角坐标系中，
的图象可能是 （ ）
 |
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
13．若A（6，m）是抛物线
上的点，F是抛物线的焦点，且AF=10，则此抛物线的焦点到准线的距离为
.
14．函数
的图象可以看成是由函数
的图象向右平移得到的，则平移的最小长度为
.
15．一个口袋中装有大小相同的2个白球和3个黑球，从中摸出一个球，放回后再摸出一个球，则两次摸出的球恰好颜色不同的概率为 .
16．正△ABC的边长为3，D、E分别为BC边上的三等分点，沿AD，AE折起，使B、C两点重合于点P，则下列结论：①AP⊥DE；②AP与面PDE所成的角的正弦值是
；③P到平面ADE的距离为；④AP与底面ADE所成的角为
其中正确的结论的序号为
（把你认为正确的结论序号都填上）.
三、解答题：本大题共6小题，满分74分.解答应写出文字说明、证明过程或演算步骤.
17．（本小题满分12分）
高三（1）班，高三（2）班每班已选出3名学生组成代表队，进行乒乓球对抗赛，比赛规则是：①按“单打、双打、单打”顺序进行三盘比赛；②代表队中每名队员至少参加一盘比赛，不得参加两盘单打比赛.已知每盘比赛双方胜出的概率均为.
（Ⅰ）根据比赛规则，高三（1）班代表队共可排出多少种不同的出场阵容？
（Ⅱ）高三（1）班代表队三盘比赛中两胜一负的概率是多少？
18．（本小题满分12分）
已知O为坐标原点，
是常数），若
（Ⅰ）求y关于x的函数解析式
（Ⅱ）若
时，
的最大值为2，求a的值并指出的单调区间.
19．（本小题满分12分）
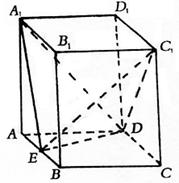
如图：直平行六面体ABCD—A1B1C1D1,底面ABCD是边长为2a的菱形，∠BAD=60°，E为AB中点，二面角A1—ED—A为60°.
|
（Ⅱ）求二面角A1—ED—C1的余弦值.
20．（本小题满分12分）
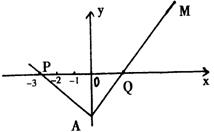
如图，已知三角形PAQ顶点P（－3，0），点A在y轴上，点Q在x轴正半轴上，
（Ⅰ）当点A在y轴上移动时，求动点M的轨迹E；
|
与轨迹E交于B、C两点，点D（1，0），若∠BDC为钝角，求k的取值范围.
21．（本小题满分12分）
已知等差数列中，
，前n项和
.
（Ⅰ）求数列的公差d；
（Ⅱ）记
，且数列的前n项和为Tn，是否存在实数M，使得
对一切正整数n都成立？若存在，求出M的最小值；若不存在，试说明理由.
22．（本小题满分12分）
已知函数对任意的实数x，y都有
（Ⅰ）若
试求的表达式；
（Ⅱ）若
时，不等式
恒成立，求实数a的取值范围.
高三期中考试数学试卷参考答案及评分标准
一、选择题：
1．B 2．C 3．A 4．D 5．D 6．B 7．B 8．C 9．D 10．C 11．C 12．D
二、填空题：
13．8； 14．
； 15．
； 16．①②③
三、解答题：
17．（Ⅰ）
……6分
（Ⅱ）设A={1班第1盘胜} B={1班第2盘胜} C={1班第3盘胜}
……12分
18．（1）
……2分
19．（Ⅰ）证明：连结BD，在菱形ABCD中：∠BAD=60°，∴△ABD为正三角形,
……1分
在直六面体ABCD—A1B1C1D1中：平面ABB1A1⊥平面ABCD且交于AB
∵ED
面ABCD ∴ED⊥面ABB1A1 ∴平面A1ED⊥平面ABB1A1……3分
（Ⅱ）解：（解法一）由（Ⅰ）知：ED⊥面ABB1A1∵A1E面ABB1A1
∴A1E⊥ED直平行六面体ABCD—A1B1C1D1中：AA1⊥面ABCD
由三垂线定理的逆定理知：AE⊥ED，∴∠A1EA为二面角A1—ED—A的平面角，∴∠A1EA=60°…4分
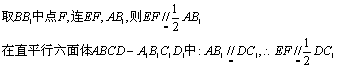
∴E、F、C1、D四点共面……5分
20．解（Ⅰ）
①……2分
②……4分
由①②
……6分
（Ⅱ）
……8分
……③
……④
y1y2=k(x1+1)·k(x2+1)=k2[x1x2+(x1+x2)+1]……⑤……10分
④⑤代入③得
……12分
21．（Ⅰ）由已知
……4分
（Ⅱ）由（Ⅰ）得
22．解：（Ⅰ）令y=1，则
……2分
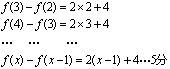
将上面各式相加得：
……7分
（Ⅱ）
