高三起点调研测试数学试卷
YCY本试卷分为第I卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分，考试用时120分钟．
试题中注明文科做的，理科考生不做；注明理科做的，文科考生不做；未作注明的，文理科考生都做．
第Ⅰ卷（选择题，共50分）
参考公式：
如果事件A、B互斥，那么 P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么 P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
球的表面积公式 
其中R表示球的半径
球的体积公式 
其中R表示球的半径
一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．集合
中元素个数为 （ ）
A．12 B．13 C．14 D．15
2．（文科）已知
= （ ）
A．
B．
C．
D．
（理）已知
= （ ）
A．－
B． C．
D．－
3．将向量
按向量
=(2，3)平移，得到的向量坐标为（1，2），那么= （ ）
A．（3，5） B．（－1，－1） C．（3，－1） D．（1，2）
4．两个事件互斥是这两个事件对立的 （ ）
A．充分但不必要条件 B．必要但不充分条件
C．充要条件 D．既不充分又不必要条件
5．（文科）在等差数列{an}中，a3=2 a5=4，则a9= （ ）
A．6 B．8 C．10 D．9
（理科）在等差数列{an}中，a2+a6+a16为定值，则{an}的前n项和Sn中一定是常数的是（ ）
A．S17 B．S15 C．S8 D．S7
6．在三棱锥P—ABC中，PA，PB，PC两两互相垂直，且PA=1，PB=PC=
，则点P到平
面ABC之距离为 （ ）
A．
B． C．
D．1
7．（文科）过定点M（－1，0）的直线被圆C：x2+y2+4x－5=0所截，所截得的最短弦长为
（ ）
A． B．2 C．4 D．8
（理科）若过定点M（－1，0）且斜率为k的直线与圆x2+y2+4x－5=0在第一象限内的部
分有交点，则k的取值范围是 （ ）
A．（－
，） B．（0，） C．（0，
） D．（0，5）
8．从1，2，…，9这9个数中，随机抽取3个不同的数，则这3个数的和为偶数的概率是
（ ）
A．
B．
C．
D．
9．设定义在实数集上的函数f(x)对任意x∈R均有f(x)+f(2－x)=1，则这个函数的图象必关于
（ ）
A．直线x=1对称 B．点（1，1）对称
C．点（1，
）对称 D．点（2，1）对称
10．现有6个人分乘两辆不同的出租车，每辆车最多乘4人，则不同的乘车方案有（ ）
A．50 B．60 C．70 D．40
第Ⅱ卷（非选择题，共100分）
二、填空题：本大题共5小题，每小题5分，共25分.把答案填在题中横线上.
11．二项式
的系数是 .
12．在条件
则函数z的最大值为 .
13．在△ABC中，若a=1，b=
，A=30°，则△ABC的面积为
.
14．（文科）设
的值域为
.
（理科）
的解集为 .
15．在双曲线C：
中，过右焦点F1作一渐近线的垂线于垂足为H，则F1H=
，H到右准线之距d= .
三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤。
16．（本小题满分12分）
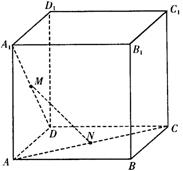
如图，在棱长为a的正方体ABCD—A1B1C1D1中，M为A1D中点，N为AC中点.
|
（2）求点M到平面BB1D1D之距.
（理科）（1）求证：MN⊥AB1；
（2）求点M到平面NB1C1的距离.
17．（本小题满分12分）
已知函数
）是R上的偶函数.
（1）求
的值；
（2）若f(x)的图象关于点
对称，且在区间
上是减函数，求f(x)的解析式.
18．（本小题满分12分）
袋中有1个白球和4个黑球，每次从中任取一个球.
（文科）（1）每次取出的球不再放回，求直到第3次才取到白球的概率.
（2）若每次取出的球是黑球则放回袋中，继续从袋中任意取出一个球，求直到第3次才取到白球的概率.
（理科）若取出一个白球，则结束，若取出一个黑球，则放回袋中继续从袋中任意取出一个球，直到取出白球为止，求取球次数ξ的概率分布列和数学期望.
19．（本小题满分12分）
（文科）已知三个实数a、b、c成等比数列，且a+b+c=2，求b的取值范围.
（理科）数列{an}满足
（1）求通项an；
（2）求
之和.
20．（本小题满分13分）
已知函数
为实数
（1）讨论f(x)在R上的奇偶性；
（2）（文科）在a=－2时，求函数
上的值域.
（理科）在a≤0时，求函数
上最大值.
21．（本小题满分14分）
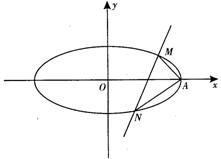
过椭圆C：
=1的右顶点A，作两条互相垂直的直线AM、AN分别交椭圆C 于M、N两点.
（1）若AM直线斜率为k，求点M的坐标；
（2）问直线MN是否过一定点，如果经过，则求出该点；否则说明理由.
|
参考答案及评分细则
第I卷（选择题，共50分）
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | (文)C (理)A | D | B | (文)B (理)B | A | (文)C (理)B | D | C | A |
二、填空题
11．－
12．2 13．
14．文 
理
15．4；0
三、解答题：
（文科）解：（1）在正方体ABCD—A1B1C1D1中，M为A1D中点，连接AD1，则M为A1D和AD1的交点
在△AD1C中，M、N分别为AD1和AC之中点
∴MN//D1C，而D1C和DC所成角为45°，又DC//AB
|
（2）∵在正方体ABCD—A1B1C1D1中，BDD1B1为体对角面
∴A1到面BD1之距即A1到B1D1之距a.
又M为A1D之中点，从而M到BD1之距a.（12分）
（理科）解：（1）在正方体ABCD—A1B1C1D1中，连接AD1
∵M为A1D中点，则M也为AD1中点
在△AD1C中，M，N分别为AD1，AC中点
∴MN//D1C，又D1C⊥DC1且DC1//AB1
∴MN⊥AB1……………………………………………………………………（6分）
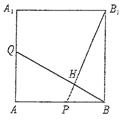
（2）设面NB1C1和AB交于点P，而N为AC中点，
则P为AB中点，且面B1C1P和面A1B1BA相互垂直，
于是M到面B1C1N之距离转化为AA1中点Q到B1P之距，
在正方形A1B1BA中，Q为A1A中点，P为AB中点
由平面几何知识而知道：QB⊥B1P，又BQ=
∴QH=
.
从而M到平面NB1C1之距为
.…………（12分）
17．解：（1）
在R上是偶函数
……（5分）
（2）由
又依据题意：
对称，
而
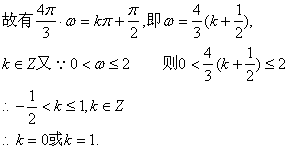
在
上单调递减.
在k=1时，f(x)=cos2x
在上不单调递减.
故所求符合题意的函数为
. ………………12分
18．（文科）解：（1）每次取出的球不再放回，直到第三次才取到白球的概率
P(ξ=3)=
………………6分
（2）若每次取出黑球则放入袋中，继续从袋中任取一个球直到第三次才取到白球，此时概率
. ……………………12分
（理科）解：第一次就取到白球P(ξ=1)=
直到第二次到取白球P(ξ=2)= 
……
直到第k次取到白球P(ξ=k)=
……
故ξ的分布列：
| ξ | 1 | 2 | 3 | … | k | … | ||
| P |
|
|
| … |
|
|
由ξ分布列满足几何分布.
因此：Eξ=
=5………………………………………………………（12分）
19．（文科）解：三实数a、b、c成等比数列，则b2=ac
由b2=ac>0 知a与c同号，有a+c=a+c
∴由a+b+c=2 知a+c=2－b
∴2－b=a+c=a+c≥2
=2b ……………（6分）
平方得(2－b)2≥4b2 即(2b－b+2)(2b+b－2)≤0
∴－2≤b≤ b≠0
故所求b取值范围为：
. ……………（12分）
（理科）解：（1）由
两边取倒数得到
由叠加原理可知：
……………………（6分）
（2）
则
设bk=k(n－k+1)=(n+1)·k－k2
于是1·n+2·（n－1）+…+n·1=（n+1）[1+2+…+n]－（12+22+…+n2）
=
……………………………………（12分）
20．解：（1）
|
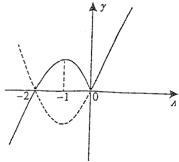
（2）（文科）在
=
画出函数草图……（8分）
函数
为减函数
有：0≤f(x)≤f(－1)=1
函数在[0，]上为增函数，
故所求值域为[0，
].…………………………（13分）
（理科）在a=0时，f(x)=xx是奇函数，在R上单调递增.
∴－1≤x≤时，f(－1)≤f(x)≤f()
此时值域范围为[－1，
]，此时最大值为.
|
画出函数草图…………（8分）
①若
最大值
可能产生于
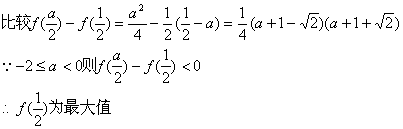
②若
≤－1<0时，即a≤－2，f(x)最大值产生于f(－1)和
比较
在
综上讨论可知：f(x)的最大值在a≤－
时为f(－1)=－1－a；
在－≤a≤0时为
……（13分）
21．解：（1）依题意AM斜率存在且不等于0，故AM直线方程为：y=k(x－2)
|
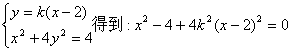
从而点M坐标为
.…………（5分）
（2）∵AM⊥AN，故AN方程：
，同理可求出N点坐标，
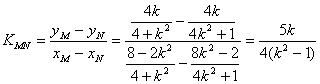………………（9分）
MN直线方程为
化简为：
故MN直线恒过定点（
，0）.……………………………………（14分）