高三第一学期期中质量联合调研数学试题
（满分：150分，完卷时间：120分钟）
一、填空题：（每小题4分，共计48分）
1、4名男生3名女生排成一排，若3名女生在一起，则不同的排法种数有 .（用数字作答）
2、已知函数
是奇函数,当
时, f（x）＝x（1＋x）,则当
时, f（x）＝
.
3、“a＝1”是“函数
在区间[1, ＋∞）上为增函数”的
条件
4、已知定义在R上的奇函数f（x）满足f（x＋2）＝－f（x）,则,f（－6）＝ .
5、函数
在区间［1，2］上存在反函数的充分必要条件是___
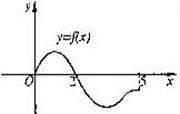
6、设奇函数f（x）的定义域为[－5，5]．若当x
[0，5]时f（x）的图象如右图，则不等式f（x）<0的解是____ _____.
7、计算：
＝__ ____．
8、从数字1，2，3，4，5中，随机抽取3个数字（允许重复）组成一个三位数，其各位数字之和等于9的概率为 （结果用最简分数表示）.
9、函数
是定义在R上的增函数，的图象过点（0，－1）和点__ ____时，能确定不等式
的解集为
10、定义集合运算：A⊙B＝｛z ︳z＝ xy（x＋y），x∈A，y∈B｝，设集合A＝｛0，1｝，B＝｛2，3｝，则集合A⊙B的所有元素之和为
11、设有两组数据：
，它们之间存在关系式：
（
，
），若这两组数据的方差分别为
，则之间的关系是
12、对a,bR,记max（a,b）＝
，求函数f（x）＝max（x＋1, x－2）（xR）的最小值是 .
二、选择题：（每小题4分，共计16分）
13、设集合
,则满足
的集合B的个数是
A．1 B．3 C．4 D．8
14、下列不等式中恒成立的有
①x2＋3>2x ②a5＋b5>a3b2＋a2b3
③a2＋b2≥2（a－b－1） ④
≥2
A．①和② B．①和③ C．③和④ D．①②③④
15、已知两点O（0,0），Q（
,b）,点P1是线段OQ的中点，点P2是线段QP1的中点，P3是线段P1P2的中点，┅，
是线段
的中点，则点的极限位置应是
A．（
,
） B．（
）
C．（
） D．（
）
16、已知复数z＝x＋yi （x,y∈R, x≥
）, 满足z－1＝x , 那么z在复平面上对应的点（x,y）的轨迹是
A．圆 B．椭圆 C．双曲线 D．抛物线
三、解答题：（共计86分）
17、（本题满分12分）
已知复数z1满足（1＋i）z1＝－1＋5i, z2＝a－2－i,其中i为虚数单位,a∈R,若
<
,求a的取值范围.
18、（本题满分12分）
讨论 
的值. 
19、（本题满分14分）
解不等式组：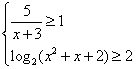
．
20、（本题满分14分）
某厂2006年拟举行促销活动，经调查测算，该厂产品的年销售量（即该厂的年产量）
万件与去年促销费
（万元）（
）满足
.已知2006年生产的固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品平均成本的1.5倍（产品成本包括固定投入和再投入两部分资金）.
（1）将2006年该产品的利润
万元表示为年促销费（万元）的函数；
（2）求2006年该产品利润的最大值，此时促销费为多少万元？
21、（本题满分16分）
已知定义域为
的函数
是奇函数。
（1）求
的值；
（2）用定义证明在
上为减函数；
（3）若对任意的
，不等式
恒成立，求
的取值范围。
22．（本题满分18分）
函数f（x）＝
（a，b是非零实常数），满足f（2）＝1，且方程f（x）＝x有且仅有一个解。
（1）求a、b的值；
（2）是否存在实常数m，使得对定义域中任意的x，f（x）＋f（m–x）＝4恒成立？为什么？
（3）在直角坐标系中，求定点A（–3,1）到此函数图象上任意一点P的距离AP的最小值。
数学试题参考答案
一、填空题：（每小题4分，共计48分）
1．720 2． x（1－x） 3．充分不必要 4．0 5．
6．
7．
8．
9．（3，1） 10．18 11．
12．
二、选择题：（每小题4分，共计16分）
13．C 14．B 15．C 16．D
三、解答题：（共计86分）
17．由题意得 z1＝
＝2＋3i, －－－－ －－－－－－ －－－－－－ －－4分
于是＝
＝
,＝
. <
得a2－8a＋7<0, 解得1<a<7. －－－－－－－－－－－－－－－－－－－－－12分
18．＝
19．
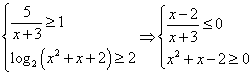
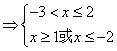
20．
（1）每件产品的成本为
元，故2006年的利润
＝
（万元），－－－－－－－－7分
（2）
－－－－－－－－－11分
等号当且仅当
，即
（万元）时成立。
答：2006年该产品利润的最大值为21万元，此时促销费为3万元。－－－14分
21、
（1）因为是奇函数，所以
＝0，即
，∴
又由f（x）＋f（－x）＝0得
－－－－－－－－－－－－－－－－－－5分
（2）
任取
，
则
所以在上为减函数；－－－－－－－－－－－－－－－－－10分
（3）因是奇函数，从而不等式：
等价于
，－－－－－－－－－－－－12分
由（2）知为减函数，由上式推得：
对一切恒成立
即
对一切恒成立，－－－－－－－－－－－－－－－14分
从而判别式
－－－－－－－－－ －－－－－－16分
22．
（1）由f（2）＝1得2a＋b＝2，又x＝0显然是方程＝x的解，
变形得
无解或有解为0，…………………3分
若无解，得a＝0，与已知矛盾，
若有解为0，则b＝1，所以a＝。
故b＝1，a＝……………………………………………………………………6分
（2）f（x）＝
，设存在常数m，使得对定义域中任意的x，f（x）＋f（m–x）＝4恒成立，取x＝0，则f（0）＋f（m–0）＝4，即
＝4，m＝－4（必要性）………8分
又m＝ –4时，f（x）＋f（–4–x）＝
＝……＝4成立（充分性） ………10分
所以存在常数m＝ –4，使得对定义域中任意的x，f（x）＋f（m–x）＝4恒成立，
（3）AP2＝（x＋3）2＋（
）2，设x＋2＝t，t≠0，……………………………13分
则AP2＝（t＋1）2＋（
）2＝t2＋2t＋2–
＋
＝（t2＋）＋2（t–
）＋2＝（t–）2＋2（t–）＋10＝（ t–＋1）2＋9， ……………………………………16分
所以当t–＋1＝0时即t＝
，
也就是x＝
时，AP min ＝ 3 ………………………………………18分