高三复习质量检测数学(1)
一、选择题(本大题共12小题,每题5分,共60分)
1.设![]() 是两个非空集合,存在元素
是两个非空集合,存在元素![]() 且
且![]() ,则下列结论中一定正确的是( )
,则下列结论中一定正确的是( ) ![]()
![]()
![]()
![]()
![]() A
A ![]()
![]()
![]() B
B ![]()
![]()
2.若角![]() 是直线的倾斜角,且
是直线的倾斜角,且![]() ,则
,则![]() ( )
( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3.在等差数列![]() 中,
中,![]() ,则此数列的前13项之和等于 ( )
,则此数列的前13项之和等于 ( ) ![]() 13
13
![]() 26
26
![]() 39
39
![]() 52
52
4. 若点![]() 在第一象限,且在直线
在第一象限,且在直线![]() 上移动,则
上移动,则![]() ( )
( )
![]() 最大值为1
最大值为1
![]() 最小值为1
最小值为1 ![]() 最大值为
最大值为![]()
![]() 既无最大值也无最小值
既无最大值也无最小值
5.已知不共线向量![]() ,
,![]() ,若A、B、C三点共线,实数
,若A、B、C三点共线,实数![]() 等于( )
等于( ) ![]()
![]()
![]()
![]()
![]()
![]()
![]() 以上都不对
以上都不对
6.已知双曲线![]() 的右焦点为
的右焦点为![]() ,以
,以![]() 为圆心的圆:
为圆心的圆:![]() 与直线
与直线![]() 相切,则双曲线的离心率为 ( )
相切,则双曲线的离心率为 ( )![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
7.函数![]() 的反函数
的反函数![]() 为 ( )
为 ( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
8.有以下四个命题:①若直线![]() 是异面直线,
是异面直线,![]() 是异面直线,则
是异面直线,则![]() 是异面直线;②若一条直线与两个平面所成的角相等,则这两个平面平行;③若一个平面内有不共线三个点到另一个平面的距离相等,则这两个平面平行;④三个平面两两相交,有三条交线,则这三条交线一定平行.以上命题中真命题个数有 ( )
是异面直线;②若一条直线与两个平面所成的角相等,则这两个平面平行;③若一个平面内有不共线三个点到另一个平面的距离相等,则这两个平面平行;④三个平面两两相交,有三条交线,则这三条交线一定平行.以上命题中真命题个数有 ( )
![]() 0个
0个
![]() 1个
1个 ![]() 2个
2个 ![]() 3个
3个
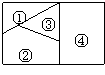
9.用5种不同颜色为下列的广告牌着色(如图),要求在①②③④四个不
同区域中相邻的区域不用同一种颜色,则不同的着色方法种数共有( )
![]() 320
320
![]() 240
240
![]() 180
180
![]() 135
135
10.已知函数![]() 在区间
在区间![]() 上是减函数,则实数
上是减函数,则实数![]() 的取值范围是( )
的取值范围是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
11.求 ![]() 等于( )
等于( )![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
12.若函数![]() 在
在![]() 上是奇函数且可导,若
上是奇函数且可导,若![]() 恒成立,且常数
恒成立,且常数![]() ,则下列不等式一定成立的是 ( )
,则下列不等式一定成立的是 ( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
二、填空题(本大题共4小题,共16分)
13.函数![]() 的定义域为
。
的定义域为
。
14.在![]() 的二面角内放一个半径为5的球,使球与两个平面各有且仅有一个公共点,则这两个点之间的球面距离等于
。
的二面角内放一个半径为5的球,使球与两个平面各有且仅有一个公共点,则这两个点之间的球面距离等于
。
15.已知点![]() 满足条件:
满足条件:![]() ,则
,则![]() 的最大值为____________。
的最大值为____________。
16.对于函数![]() ,给出下列四个命题:
,给出下列四个命题:
①存在实数![]() ,使
,使![]() ;
;
②存在实数![]() 恒成立;
恒成立;
③存在![]() ,使函数
,使函数![]() 的图像关于
的图像关于![]() 轴对称;
轴对称;
④函数![]() 的图像关于点
的图像关于点![]() 对称;
对称;
其中正确命题的序号是________________。
三、解答题(本大题共6小题,共74分)
17.(本大题满分12分)已知![]() ,
,![]() ,记函数
,记函数![]() 。
。
(Ⅰ)求函数![]() 的最小正周期及最值; (Ⅱ)当
的最小正周期及最值; (Ⅱ)当![]() 时,求函数
时,求函数![]() 的值域。
的值域。
18.(本大题满分12分)投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分,经过多次试验,某生投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋。(Ⅰ)求该人在4次投掷中恰有三次投入红袋的概率。(Ⅱ)求该人两次投掷后得2分的概率。
19.(本大题满分12分)设![]() (
(![]() 都是整数)奇函数,且
都是整数)奇函数,且![]() 在
在![]() 上是单调递增。
上是单调递增。
(Ⅰ)求![]() 的解析式;
(Ⅱ)试判断函数
的解析式;
(Ⅱ)试判断函数![]() 在
在![]() 上的单调性,并证明。
上的单调性,并证明。
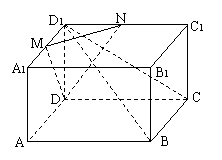 20.(本大题满分12分)已知正四棱柱
20.(本大题满分12分)已知正四棱柱![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() 平面
平面![]() 。(I)求证:
。(I)求证:![]() 平面
平面![]() ;
;
(II)求二面角![]() 的平面角的正切值。
的平面角的正切值。
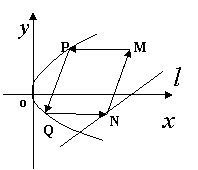
21.(本大题满分12分)抛物线有光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.今有抛物线![]() ,一光源在点
,一光源在点![]() 处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点
处,由其发出的光线沿平行于抛物线的对称轴的方向射向抛物线上的点![]() ,反射后又射向抛物线上的点
,反射后又射向抛物线上的点![]() ,再反射后,又沿平行于抛物线的对称轴方向射出,途中遇到直线
,再反射后,又沿平行于抛物线的对称轴方向射出,途中遇到直线![]() 上的点
上的点![]() ,再反射后又射回到点
,再反射后又射回到点![]() .(如图所示)(I)设
.(如图所示)(I)设![]() 两点坐标分别为
两点坐标分别为![]() ,证明:
,证明:![]() ;(II)求此抛物线方程;
;(II)求此抛物线方程;
 (III)试判断在抛物线上是否存在一点,使该点与点
(III)试判断在抛物线上是否存在一点,使该点与点![]() 关于
关于![]() 所在的直线对称?若存在,请求出此点的坐标;若不存在,请说明理由.
所在的直线对称?若存在,请求出此点的坐标;若不存在,请说明理由.
22.(本大题满分14分)由原点O向三次曲线![]() 引切线,切于点P1(x1,y1)(O,P1两点不重合),再由P1引此曲线的切线,切于点P2(x2,y2)(P1,P2不重合).如此继续下去,得到点列
引切线,切于点P1(x1,y1)(O,P1两点不重合),再由P1引此曲线的切线,切于点P2(x2,y2)(P1,P2不重合).如此继续下去,得到点列![]() (1)求x1;(2)求
(1)求x1;(2)求![]() 满足的关系式;(3)若a>0,试判断
满足的关系式;(3)若a>0,试判断![]() 与a的大小关系并说明理由.
与a的大小关系并说明理由.
一、选择题(每题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | C | A | B | B | D | A | C | D | D | A |
二、填空题(每题4分,共16分)
13、![]() (理科)
(理科)![]() 14、
14、 ![]()
15、15
16、(文)③④(理)![]()
三、解答题
17、解:(Ⅰ)![]() -----------------------2分
-----------------------2分
=![]() ---------------------------4分
---------------------------4分
=![]() -------------------------6分
-------------------------6分
所以
![]() ,
,![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() -----------------------7分
-----------------------7分
(Ⅱ)当![]() ,即
,即![]() ,有
,有![]() ------------------10分
------------------10分
所以当![]() ,函数
,函数![]() 的值域为
的值域为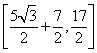 -----------------------12分
-----------------------12分
18、解:(Ⅰ)依题意知:![]() 是奇函数,可得
是奇函数,可得![]() ---------------1分
---------------1分
又![]() 因为
因为![]() 都是整数,所以
都是整数,所以![]() ------------------3分
------------------3分
故:![]() ------------------------4分
------------------------4分
(Ⅱ)![]()
![]() ,
,
![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减-------------------6分
上单调递减-------------------6分
证明如下:设![]() ,则
,则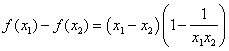 --------------8分
--------------8分
因为![]() ,所以
,所以![]() ,故
,故![]()
![]() 上单调递增;------------------------------------------10分
上单调递增;------------------------------------------10分
同理可证![]() 上单调递减.------------------------------------12分
上单调递减.------------------------------------12分
(理科可直接用导数证明)
19、解:(Ⅰ)求该人在4次投掷中恰有三次投入红袋的概率。
(Ⅱ)(文科)分别求该人两次投掷后得0分、1分、2分的概率。
(理科)求该人两次投掷后得分![]() 的数学期望。
的数学期望。
解:(Ⅰ)、“飞碟投入红袋”,“飞碟投入蓝袋”,“飞碟不入袋”分别记
为事件A,B,C。则由题意知:![]() ---------------3分
---------------3分
因每次投掷飞碟为相互独立事件,故4次投掷中恰有三次投入红袋的概率为;
![]() -------------------------------6分
-------------------------------6分
(Ⅱ)、两次投掷得分![]() 的得分可取值为0,1,2,3,4则:
的得分可取值为0,1,2,3,4则:
![]() -------------------------------------- 7分
-------------------------------------- 7分
![]() --------------------------------------9分
--------------------------------------9分
![]() --------------------------------------12分
--------------------------------------12分
![]() ;
;![]() --------------------------------------理科10分
--------------------------------------理科10分
![]() --------------------------------------12分
--------------------------------------12分
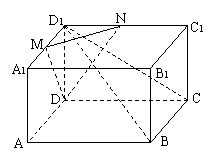 20、解:(理科)(1)如图连接
20、解:(理科)(1)如图连接![]() ,交
,交![]() ,再连
,再连![]()
![]()
![]()
又![]()
故![]() 为
为![]() 在面
在面![]() 的射影,由三垂线定理
的射影,由三垂线定理 ![]()
所以![]() 即为二面角
即为二面角![]() 的平面角---------------------------3分
的平面角---------------------------3分
在矩形![]() 中,因
中,因![]() ,故
,故![]() ~
~![]()
![]() 得
得![]()
![]()
![]()
![]() --------------------------------------------6分
--------------------------------------------6分
(2)如图由(1)知![]() ,
,![]()
![]() 面
面![]() 即面
即面![]() 面
面![]() ,其中BP为交线
,其中BP为交线
故![]() 到面
到面![]() 的距离即为
的距离即为![]() 到BP的距离
到BP的距离
在矩形![]() 中,设
中,设![]() 到BP的距离为
到BP的距离为![]() -----------9分
-----------9分
![]()
在![]() 中,
中,![]()
![]() --------12分
--------12分
(文科)在正四棱柱![]() 中,
中,![]() ,
,![]()
![]() ,所以
,所以![]() ,又因为
,又因为![]() 平面
平面![]() ,所以
,所以![]() ,故
,故![]() 平面
平面![]() ----------------------4分
----------------------4分
(第二问参照理科标准给分)
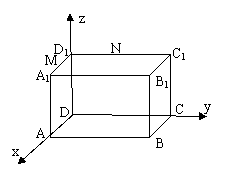
另解(1)如图建立坐标系,设![]()
故![]() 、
、![]() 、
、![]() 、
、![]()
![]()
![]()
![]() 即
即![]()
![]()
向量![]() 与面
与面![]() 垂直
垂直
设![]() 与面BDN垂直,则
与面BDN垂直,则![]()
即![]()
![]()
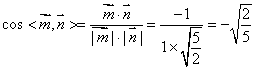
设所求二面角为![]() ,则
,则![]() ,
, ![]()
(2)由![]()
![]() 在向量
在向量![]() 方向上的投影为
方向上的投影为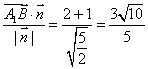
所以![]() 到面
到面![]() 的距离为
的距离为![]()
21、解:(1)由抛物线的光学性质知光线PQ必过抛物线的焦点![]() ,当直线PQ的倾斜角不为
,当直线PQ的倾斜角不为![]() 时,设PQ的方程为:
时,设PQ的方程为:![]() ①
------------------------------------------------2分
①
------------------------------------------------2分
代入方程:![]() 中,整理可得:
中,整理可得:![]() ,由根与系数的关系可得
,由根与系数的关系可得![]() ----3分
----3分
当直线PQ的倾斜角为![]() 是,将
是,将![]() 代入抛物线方程,可得
代入抛物线方程,可得![]() ,同样满足
,同样满足![]() ------4分
------4分
(2)因为光线QN经直线![]() 反射后又射向M点,所以MN与QN关于直线
反射后又射向M点,所以MN与QN关于直线![]() 反射对称,设点
反射对称,设点![]() 关于
关于![]() 的对称点为
的对称点为![]() 则
则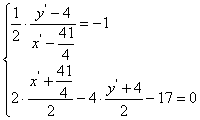
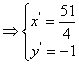 -------------6分
-------------6分
![]() 直线QN的方程为
直线QN的方程为![]() ,Q点纵坐标
,Q点纵坐标![]() ,因为点P纵坐标为
,因为点P纵坐标为![]() ,由(1)可知
,由(1)可知![]() ,
,
即:![]() ,所以
,所以![]() -------------------------------------------------------------8分
-------------------------------------------------------------8分
(3)将![]() 代入
代入![]() ,可知P点坐标为
,可知P点坐标为![]() ;将
;将![]() 代入直线
代入直线![]() 可得
可得![]() ,所以直线PN的方程为
,所以直线PN的方程为 ![]() ,设点
,设点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,则
,则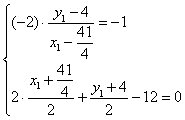
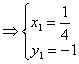 -------------------------------------10分
-------------------------------------10分
将![]() 代入抛物线方程
代入抛物线方程![]() ,原式成立,
,原式成立,
故存在一点![]() 满足题意。-----------------------------------------------------12分
满足题意。-----------------------------------------------------12分
22、解:(1)解:由![]()
过曲线上点P1(x1,y1)的切线L1的斜率为![]()
![]()
又![]()
![]() ----------------------------------4分
----------------------------------4分
(2)过曲线上的点![]() 的切线方程是:
的切线方程是:
![]()
![]() 过曲线上点
过曲线上点![]()
故![]()
即:![]()
![]()
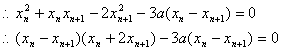
![]() -------------------------------------------------------------8分
-------------------------------------------------------------8分
(3)由(2)得:![]()
故数列![]() 为首项,公比为
为首项,公比为![]() 的等比数列.
的等比数列.
![]()
![]() --------------------------------------------------------12分
--------------------------------------------------------12分
∵![]() ∴当n为偶数时:
∴当n为偶数时:![]()
当n为奇数时:![]() --------------------14分
--------------------14分