高三级第三次周日考试数学（理科）试题卷
总分150分
一、选择题（每小题只有一个正确选项，把正确选项涂在答题卡的相应位置。
共8×5＝40分)
1、已知集合
,若
，则符合条件的实数m组成的集合是( )
A、
B、
C、
D、
2、对于平面
和共面的直线
、
下列命题中真命题是（ ）
A．若
则
B．若
则
C．若
则 D．若、
与所成的角相等，则
3、设A、B是两个集合，定义
，
R}，则M－N= （ ）
A．[－3，1] B．[－3，0） C．[0，1] D．[－3，0]
4、不等式
成立的充分不必要条件是（ ）
A．
或
B．
或
C．
D．
5、设
是函数
的导函数,
的图象如图所示，则
的图象最有可能的是（ ）
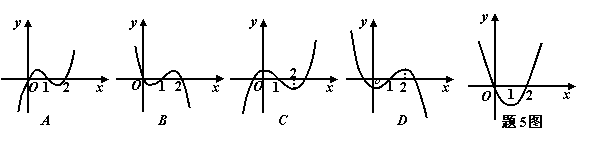
6、若平面四边形
满足
,
,则该四边形一定是（ ）
A．直角梯形 B．矩形 C．菱形 D．正方形
7、如图，一个空间几何体的主视图、左视图、俯视图为全等
的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的体积为 ( )
1
8、为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文
对应密文
,例如,明文
对应密文
.当接收方收到密文
时,则解密得到的明文为（ ）
A．
B．
C．
D．
二填空题（把正确答案填在答题卡的相应位置，填在试卷上无效。共6×5＝30分。）
9、已知向量
，
，且
，则x= __________．
10、函数
的最小正周期是 .
11、在约束条件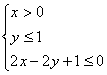
下，目标函数
=
的最大值为
.
12、已知
,
则
的最大值为
13、某公司一年购买某种货物400吨，每次都购买
吨，运费为4万元/次，一年的总存储费用为
万元，要使一年的总运费与总存储费用之和最小，则
吨．
14、若函数
的值域为R，则实数a的取值范围是__________
三、解答题（把解答过程写在答题卡的相应位置, 总共80分）
15、（本小题满分12分）
在△
中，
，
，
是三角形的三内角，a，b，
是三内角对应的三边长，
已知
（Ⅰ）求角的大小；
（Ⅱ）若
，求角的大小.
16、（本小题满分12分，每小题4分）
根据下面各个数列
的首项和递推关系，求其通项公式
⑴
⑵
⑶
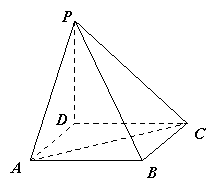17、（本小题满分14分）
如图,四棱锥P-ABCD是底面边长为1的正方形，
PD⊥BC,PD=1,PC=
.
(Ⅰ)求证:PD⊥面ABCD；
(Ⅱ)求二面角A－PB－D的大小.
18、（本小题满分1４分第一、第二小问满分各７分）
已知向量
满足
,且
,令
，
（Ⅰ）求
（用
表示）；
（Ⅱ）当
时，
对任意的
恒成立，求实数的取值范围。
19、（本小题满分14分，第一小问满分4分，第二、第三小问满分各5分）
已知定义域为
的函数满足
（I）若
,求
；又若
,求
；
（II）设有且仅有一个实数
,使得
,求函数的解析表达式.
20、（本小题满分14分）
已知二次函数
, 满足
且
的最小值是
.
（Ⅰ）求的解析式;
（Ⅱ）设直线
,若直线
与的图象以及
轴这二条直线和一条曲线所围成封闭图形的面积是
, 直线与的图象以及直线
这二条直线和一条曲线所围成封闭图形的面积是
,已知
,当
取最小值时,求
的值.
（Ⅲ）已知
, 求证: 
.
高三级第三次周日考试数学（理科）试题卷参考答案
参考答案
一. 选择题
1C 2C 3B 4D 5C 6C 7 D ８C
二.填空题
９、2 10 、
11、2 12、 6 13. 20 14．(0,1)∪
三 解答题
15．（本小题满分12分）
解：（Ⅰ）在△ABC中，
…………6分
（Ⅱ）由正弦定理,又,故
…………8分
即: 
故△ABC是以角C为直角的直角三角形……………10分
又
…………………………………………………………12分
16．（本小题满分12分）
解：（1）
，
，
（2）
=
又解：由题意，
对一切自然数成立，
（3）
是首项为
公比为
的等比数列，
说明：本题考查求通项公式的几种方法：迭加法、迭乘法、构造法。
17．（本小题满分14分）
(Ⅰ)证明:
,
.……2分
又
,……4分
∴ PD⊥面ABCD………6分
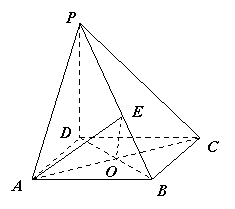
(Ⅱ)解:连结BD,设BD交AC于点O,
过O作OE⊥PB于点E,连结AE,
∵PD⊥面ABCD, ∴
,
又∵AO⊥BD, ∴AO⊥面PDB.
∴AO⊥PB,
∵
,
∴
,从而
,
故
就是二面角A－PB－D的平面角.……………………10分
∵ PD⊥面ABCD, ∴PD⊥BD,
∴在Rt△PDB中, 
,
又∵
, ∴
,………………12分
∴ 
.
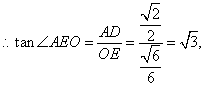故二面角A－PB－D的大小为60°. …………………14分
（也可用向量解）
18（本小题满分1４分）
（Ⅰ）由题设得
，对
两边平方得
展开整理易得
------------------------6分
（Ⅱ）
，当且仅当＝1时取得等号.
欲使对任意的恒成立，等价于
即
在
上恒成立，而
在上为单调函数或常函数，
所以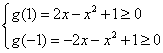
解得
故实数的取值范围为
---------------------------------14分
19．（本小题满分14分，第一小问满分6分，第二小问满分8分）
（I）因为对任意
有
,
所以
,又,从而
若,则
,即
----------------------------6分
（II）因为对任意,有
又有且仅有一个实数,使得,故对任意,有
在上式中令
,有
又因为,所以
,故
或
若,则
,但方程
有两个不相同实根,与题设条件矛盾,故
.
若,则有
,易验证该函数满足题设条件.
综上,所求函数的解析表达式为 ---------------------------14分
20．（本小题满分14分）
解: (1)由二次函数图象的对称性, 可设
,又
故
…………………3分
(2) 据题意, 直线与的图象的交点坐标为
,由定积分的几何意义知
………5分
=
=
…………………………………………………………7分
而
令
或
(不合题意,舍去)
当
……………8分
故当
时,有最小值.………………………………………………………9分
(3) 
的最小值为
……①
……②……………………………11分
①+②得: 
………③
又
…………………12分
由均值不等式和③知:
…………………………13分
故
……14分