高三级理科数学月考试题4
总分150分
一、选择题(![]() )
)
1.
函数![]() 的最小正周期为( )
的最小正周期为( )
A)![]() B)
B)![]() C)
C)![]() D)
D)![]()
2.
已知![]() ,若
,若![]() ,则
,则![]() 的值是( )
的值是( )
A)5 B)![]() C)
C)![]() D)
D)![]()
3.
函数![]() 的定义域为( )
的定义域为( )
A)![]() B)
B)![]() C)
C)![]() D)
D)![]()
4.
设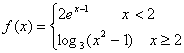 ,则
,则![]() 的值为( )
的值为( )
A)![]() B)
B)![]() C)
C)![]() D)
D)![]()
5.
已知数列![]() 满足
满足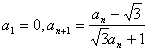
![]() ,则
,则![]() ( )
( )
A)0 B)![]() C)
C)![]() D)
D)![]()
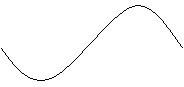
6. 下列函数中,图象的一部分如右图所示的是( )
![]()
![]()
![]() A)
A)![]()
![]()
![]()
![]() B)
B)![]()
![]()
![]()
![]()
![]()
![]()
![]() C)
C)![]()
D)![]()
7.
已知等比数列![]() 的公比
的公比![]() ,其前
,其前![]() 项的和为
项的和为![]() ,则
,则![]() 与
与![]() 的大小
的大小
关系为( )
A)![]() >
>![]() B)
B)![]() =
=![]() C)
C)![]() <
<![]() D)不能确定
D)不能确定
8.
![]() 且
且![]() ,则
,则![]() 的
的
最小值为( )
A)![]() B)
B)![]() C)
C)![]() D)
D)![]()
二、填空题(![]() )
)
9.不等式![]() 的解集是____________
的解集是____________
10.已知![]() ,若
,若![]() ,则
,则![]() ____________
____________
11.若![]() 有极大值和极小值,则
有极大值和极小值,则![]() 的取值
的取值
范围是____________
12.函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() ,
,
则![]() ____________
____________
13.对正整数![]() ,设曲线
,设曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,
,
则数列![]() 的前
的前![]() 项和公式是____________
项和公式是____________
14.设![]() 满足约束条件
满足约束条件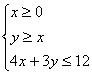 ,则
,则![]() 的取值范围是____________
的取值范围是____________
三、 解答题(共80分)
15.(12分)已知向量![]() ,
,![]() 与
与![]() 为共线向量且
为共线向量且![]()
Ⅰ)求![]() 的值
的值
Ⅱ)求![]() 的值
的值
16.(13分)已知定义域为R的函数![]() 是奇函数,
是奇函数,
Ⅰ)求![]() 的值
的值
Ⅱ)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
17.(13分)已知![]() 三内角A、B、C的对边分别为
三内角A、B、C的对边分别为![]() ,关于
,关于![]() 的不等式
的不等式![]() 的解集为空集
的解集为空集
Ⅰ)求C的最大值
Ⅱ)已知![]() ,
,![]() 的面积
的面积![]() ,当C最大时,求
,当C最大时,求![]()
18.(14分)已知等差数列![]() 中,公差
中,公差![]() ,其前
,其前![]() 项和为
项和为![]() 且满足
且满足![]()
Ⅰ)求数列![]() 的通项公式
的通项公式
Ⅱ) 由通项公式![]() 得出的数列
得出的数列![]() 如果也是等差数列,求非零常数C
如果也是等差数列,求非零常数C
Ⅲ) 求![]() 的最大值
的最大值
19.(14分)Ⅰ)已知函数![]() 在(0,1)上是增函数,求实数
在(0,1)上是增函数,求实数![]() 的取值范围
的取值范围
Ⅱ)在Ⅰ)的结论下,设![]()
![]() ,求函数
,求函数![]() 最小值。
最小值。
20.(14分)已知点P在曲线![]() 上,曲线C在点P处的切线与函数
上,曲线C在点P处的切线与函数![]() 的图象交于点A,与
的图象交于点A,与![]() 轴交于点B,设点P的横坐标为
轴交于点B,设点P的横坐标为![]() ,点A,B的横坐标分别为
,点A,B的横坐标分别为![]() ,记
,记![]()
Ⅰ)求![]() 的解析式
的解析式
Ⅱ)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式
的通项公式
Ⅲ)在Ⅱ)的条件下,当![]() 时,证明不等式
时,证明不等式![]()
高三级理科数学月考试题4
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | D | B | D | B | D | A | D |
二、填空题
9、![]() 10、
10、![]() 11、
11、![]() 12、
12、![]()
13、![]() 14、
14、![]()
三、解答题
15、解:(Ⅰ)![]() 与
与![]() 为共线向量,
为共线向量,![]()
即![]() ……………………………..5分
……………………………..5分
(Ⅱ)![]() ,
,![]() …………………….8分
…………………….8分
![]()
![]()
又![]() ,
,![]() …………………..10分
…………………..10分
因此,![]() ……………………12分
……………………12分
16、解:(Ⅰ)因为![]() 是奇函数,所以
是奇函数,所以![]() ,即
,即![]() ,解得
,解得![]()
从而有![]() …………………….3分
…………………….3分
又由![]() 知
知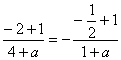 ,解得
,解得![]() …………………….6分
…………………….6分
(Ⅱ)解:由(Ⅰ)知![]()
由上式易知![]() 在
在![]() 上为减函数
……………………..8分
上为减函数
……………………..8分
又因![]() 是奇函数,从而不等式
是奇函数,从而不等式![]()
等价于![]()
因![]() 是减函数,由上式推得
是减函数,由上式推得![]() …………………..11分
…………………..11分
即对一切![]() ,有
,有![]()
从而判别式![]() ,解得
,解得![]() …………………..13分
…………………..13分
17、解:(1)![]() 的解集是空集
的解集是空集
![]() 且
且![]() ,解得
,解得![]() ……………………...4分
……………………...4分
又![]() ,所以C的最大值为
,所以C的最大值为![]() ……………………...6分
……………………...6分
(2)![]() ,
,![]() ,
,
![]() ……………………...9分
……………………...9分
而![]()
![]() …………………...11分
…………………...11分
![]()
![]() …………………...13分
…………………...13分
18、解:(1)![]() 为等差数列,
为等差数列,![]()
又![]()
![]() 是方程
是方程![]() 的两实数根
的两实数根
又公差![]() ,
,![]() ,
,![]()
![]() …………………….4分
…………………….4分
(2)由(1)知![]() …………………….6分
…………………….6分
![]() ,
,![]() ,
,![]() ,
,![]()
![]() 是等差数列,
是等差数列,![]() …………………..8分
…………………..8分
即![]() ,
,![]()
![]() 舍去),故
舍去),故![]() …………………..9分
…………………..9分
(3)由(2)得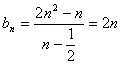
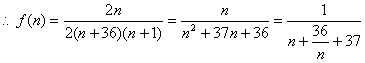 …………………12分
…………………12分
由函数的单调性可知:![]() 时,
时,![]()
![]() 的最大值为
的最大值为![]() ………………….14分
………………….14分
19、解:(Ⅰ)![]() ………………….2分
………………….2分
![]() 在(0,1)上是增函数
在(0,1)上是增函数
![]() 在(0,1)上恒成立,即
在(0,1)上恒成立,即![]() 恒成立
恒成立
![]() (当且仅当
(当且仅当![]() 时取等号)
………………….4分
时取等号)
………………….4分
所以![]() ………………….5分
………………….5分
当![]() 时,易知
时,易知![]() 在(0,1)上也是增函数,所以
在(0,1)上也是增函数,所以![]() ………………6分
………………6分
(Ⅱ)设![]() ,则
,则![]()
![]()
当![]() 时,
时,![]() 在区间[1,3]上是增函数
在区间[1,3]上是增函数
所以![]() 的最小值为
的最小值为![]() ………………….10分
………………….10分
当![]() 时,
时,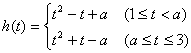
因为函数![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上也是增函数,所以
上也是增函数,所以![]() 在[1,3]上为增函数
在[1,3]上为增函数
所以![]() 的最小值为
的最小值为![]() ………………….13分
………………….13分
所以,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,当
,当![]() 时,
时,![]() 的最小值为
的最小值为![]() …14分
…14分
20、解:(Ⅰ)![]() 的导数
的导数![]() ,又
,又![]() 点P的坐标为
点P的坐标为![]() ,
,![]() 曲线C在P点的切线的斜率为
曲线C在P点的切线的斜率为![]() ,
,
则该切线方程为![]() ,令
,令![]() ,得
,得![]()
由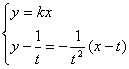 ,得
,得![]() ,
,![]() …….3分
…….3分
因此,![]() 的解析式为:
的解析式为:![]() ………….4分
………….4分
(Ⅱ)![]() 时,
时,![]() ,
,![]() ,即
,即![]()
①当![]() 时,
时,![]() ,
,![]() 数列
数列![]() 是以0为首项的常数数列,则
是以0为首项的常数数列,则![]()
②当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列, ……………..7分
为公比的等比数列, ……………..7分
![]() ,解得
,解得![]()
综合①、②得![]() …………….9分
…………….9分
(Ⅲ)![]() ,
,![]() ,
,![]()
![]() ,
,![]()
则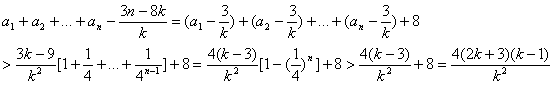
![]() ,
,![]()
因此,不等式![]() 成立
………………….14分
成立
………………….14分