高三级数学模拟试卷(-)
(理工类)
(集合与逻辑、函数、导数、积分)
命题:广东实验中学 江秋民 杨庆元 刘军凤 翁之英
华南师附中 罗 华 广州市第六中学 李伟文
考生注意:
1. 本试卷共150分,考试时间为120分钟。
2. 答题前,考生务必将密封线内的项目填写清楚。
3. 请将答案填在试卷后面的答题卷上。
一、选择题:本大题共有8个小题,每小题5分,共40分。在每小题给出的四个选项中,恰有一项是符合题目要求的。
1.已知全集为![]() ,则有
,则有
A ![]() B
B ![]() C
C ![]() D
D ![]()
2.函数![]() 的定义域是
的定义域是
A (0,![]() ] B (-∞,
] B (-∞,![]() ] C (0,
] C (0,![]() ] D (-∞,
] D (-∞,![]() ]
]
3.设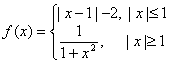 ,则
,则![]()
A ![]() B
B
![]() C
C ![]() D
D
![]()
4.下列函数既是奇函数,又在[-1,1]上单调递减的是
A ![]() B
B ![]() C
C ![]() D
D ![]()
5.设![]() ,利用课本中推导等差数列前
,利用课本中推导等差数列前![]() 项和公式的方法,可求得
项和公式的方法,可求得
![]() 的值是
的值是
A ![]() B
B ![]() C
C ![]() D
D![]()
6.若![]() ,定义
,定义![]() 例如
例如![]() ,则
,则![]() 函数的奇偶性为
函数的奇偶性为
A ![]() 为偶函数,但不是奇函数
B
为偶函数,但不是奇函数
B ![]() 为奇函数,但不是偶函数
为奇函数,但不是偶函数
C ![]() 既是奇函数,又是偶函数
D
既是奇函数,又是偶函数
D ![]() 既不是奇函数,又不是偶函数
既不是奇函数,又不是偶函数
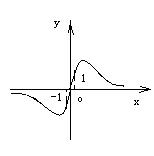 7.若函数
7.若函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的取值范围为
的取值范围为
A (-∞,-1) B (1,2) C (-1,2) D (0,2)
8.已知定义在R上的函数![]() 满足
满足![]() ,且
,且![]() ,则
,则
![]()
A —2 B —1 C 0 D 1
二、填空题:本大题共6小题,每小题5分,共30分,请把答案填写在答题卷中对应题号的横线上。
9.函数![]() 的图象F按向量
的图象F按向量![]() 平移到G,则图象G与函数图象M关于
平移到G,则图象G与函数图象M关于![]() 对称,则M的函数解析式为
。
对称,则M的函数解析式为
。
10.有两个命题:1不等式![]() 的解集是R;2函数
的解集是R;2函数![]() 是减函数,若这两个命题中有且只有一个真命题,则实数
是减函数,若这两个命题中有且只有一个真命题,则实数![]() 的取值范围是
。
的取值范围是
。
11.对于集合M、N,定义M—N=![]() ,设
,设![]() ,
,![]() 则
则![]() 。
。
12.已知![]() ,若
,若![]() 对
对![]() 恒成立,实数
恒成立,实数![]() 的取值范围是
。
的取值范围是
。
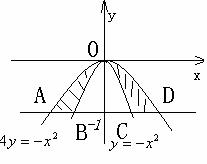
13.如图,由两条曲线![]() 及直线
及直线![]() 所围成的图形的面积为
。
所围成的图形的面积为
。
 14.已知函数
14.已知函数![]() 。给出下列命题:
。给出下列命题:
1![]() 必是偶函数;2当
必是偶函数;2当![]() 时,
时,![]() 的图象必关于直线
的图象必关于直线![]() 对称;3若
对称;3若![]() 上是增函数;4
上是增函数;4![]() 有最大值
有最大值![]() 。
。
其中正确的序号是 。
三、解答题:本大题共6小题,共80分,解答时应写出文字说明、证明过程或演算步骤。
15.(本小题12分)
已知![]() ,若
,若![]() 是
是![]() 的充分条件,求实数
的充分条件,求实数![]() 的范围。
的范围。
16.(本小题12分)
已知![]() 的图象过点(—2,—3),且满足
的图象过点(—2,—3),且满足![]() 设
设
![]() 。
。
(Ⅰ)求![]() 的表达式;
的表达式;
(Ⅱ)是否存在正实数![]() ,使
,使![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数?若存在,求出
上是减函数?若存在,求出![]() ;若不存在,请说明理由。
;若不存在,请说明理由。
17.(本小题14分)
设函数![]() 的图象关于原点对称,
的图象关于原点对称,![]() 的图象在点
的图象在点![]() (1,
(1,![]() )处的切线的斜率为—6,且当
)处的切线的斜率为—6,且当![]() 时
时![]() 有极值。
有极值。
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ)若![]() ,求证:
,求证:![]() 。
。
18.(本小题14分)
设关于![]() 的一元二次方程
的一元二次方程![]() 两个根为
两个根为![]() 、
、![]() ,函数
,函数![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)证明![]() 是
是![]() 上的增函数;
上的增函数;
(Ⅲ)当![]() 为何值时,
为何值时,![]() 在区间
在区间![]() 上的最大值与最小值之差最小。
上的最大值与最小值之差最小。
19.(本小题14分)
已知二次函数![]()
(Ⅰ)若任意![]() ,且
,且![]() ,都有
,都有![]() ,求证:关于
,求证:关于![]() 的方程
的方程![]() 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于![]() ;
;
(Ⅱ)若关于![]() 的方程
的方程![]() 在
在![]() 的根为
的根为![]() ,且
,且![]() 成等差数列,设函数
成等差数列,设函数![]() 的图象的对称轴方程为
的图象的对称轴方程为![]() ,求证:
,求证:![]() 。
。
20.(本小题14分)
已知定义在(—1,1)上的函数![]() 满足
满足![]() ,且对
,且对![]() 时,有
时,有![]() (Ⅰ)判断
(Ⅰ)判断![]() 在(—1,1)上的奇偶性,并加以证明;
在(—1,1)上的奇偶性,并加以证明;
(Ⅱ)令![]() ,求数列{
,求数列{![]() }的通项公式;
}的通项公式;
(Ⅲ)设![]() 为数列{
为数列{![]() }的前
}的前![]() 项和,问是否存在正整数
项和,问是否存在正整数![]() ,使得对任意的
,使得对任意的![]() ,有
,有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值,若不存在,则说明理由。
的最小值,若不存在,则说明理由。
高三级数学模拟试卷(-)答案
一、选择题:(每小题5分,共40分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | C | B | D | D | A | B | C |
第Ⅱ卷(非选择题 110分)
二.填空题(每题5分共30分)
| 9. 11._(—∞, 13.__ | 10.__[1,2)______; 12. 14.________3______________。 |
三.解答题 答题说明:解答题应写出必要的文字说明,证明过程或演算步骤
15.(本题满分12分)
【解】![]() ,
, ![]() :
:![]() 或
或![]() 。
。
设![]()

16.解:(1)

17.解 (1) ![]() 关于原点对称,
关于原点对称,![]() 由
由![]() 恒成立有
恒成立有![]() 则
则![]() , 又
, 又![]() ,
, ![]()
故![]()
![]() ……6分
……6分
(2)![]()
![]()
当![]() 时,
时,![]() 。
。![]() 在[-1,1]上递减,而
在[-1,1]上递减,而![]()
![]() 即
即![]()
![]()
![]() 同理,
同理,![]()
![]() ,故
,故![]()
18.解:(1)由已知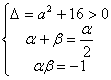
![]()
![]()
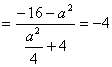
(2)![]() 设
设![]() =
= ![]() ,
,![]() ,由题设可知任取
,由题设可知任取![]() ,都有
,都有![]() >0,
>0, ![]() .
.![]() 故
故![]() 在
在![]() 上的增函数;
上的增函数;
(3) 因为![]() ,且
,且![]() 在
在![]() 上的增函数,
上的增函数,![]()
![]()
![]() .当且仅当
.当且仅当![]() 时等号成立.
时等号成立. ![]()
![]() ,又
,又![]() 即
即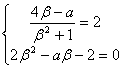 ,解得:
,解得:![]()
19.解: (Ⅰ)![]()
![]()
![]()
![]()
![]()
整理得,![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() 故至少有一个不是0,
故至少有一个不是0,![]()
故方程有两个不相等的实数根
令![]() ,则
,则![]() ,又
,又![]() ,则
,则![]()
故方程![]() 必有一个根属于
必有一个根属于![]() ;
;
(Ⅱ)![]() 方程
方程![]() 在
在![]() 内根为
内根为![]() ,
, ![]()
![]()
![]()
![]()
![]() 成等差数列,则
成等差数列,则![]() ,
,![]()
![]() ,
,
故![]()
20 解:(Ⅰ)令![]() ,得,
,得,![]() ,又当
,又当![]() 时,
时,![]() ,即
,即![]()
故对任意![]() (—1,1)时,都有
(—1,1)时,都有![]() ,故
,故![]() 在(—1,1)上的奇函数 3分
在(—1,1)上的奇函数 3分
(Ⅱ){![]() }满足
}满足![]()
![]() 否则
否则![]() ,依此类推可得到
,依此类推可得到![]() 与已知矛盾),
与已知矛盾),![]()
![]()
![]()
因为![]() 在(—1,1)上的奇函数,
在(—1,1)上的奇函数,![]()
![]()
![]()
![]() ,即
,即![]()
![]() {
{![]() }是以1为首项、公比为2的等比数列。
}是以1为首项、公比为2的等比数列。
![]()
![]() =
=![]() 8分
8分
(Ⅲ)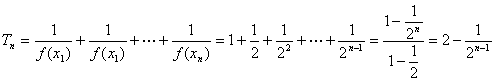
假设存在正整数![]() ,使得对任意的
,使得对任意的![]() ,有
,有![]() 成立,即
成立,即![]() 对于
对于![]() 恒成立。只须
恒成立。只须![]() ,即
,即![]() 。故存在正整数
。故存在正整数![]() ,使得对任意的
,使得对任意的![]() ,有
,有![]() 成立。此时
成立。此时![]() 的最小值为10。
的最小值为10。