高三联合诊断性考试数学理科试卷
本试卷分第I卷（选择题）和第II卷（非选择题）两部分。共150分，考试时间120分钟。
第I卷（选择题，共60分）
一、选择题：（本大题12个小题，每小题5分，共60分）
1．如果A={xx>－1}，那么正确的结论是 （ ）
A．0
A B．{0}∈A C．{0} 
A
D．
∈A
2．给定两个向量
平行，则x的值等于 （ ）
A．1 B．
C．2 D．
3．对函数
作代换x=g(t)，则总不改变f(x)值域的代换是 （ ）
A．
B．
C．g(t)=(t－1)2 D．g(t)=cost
4．数列{an}是等差数列，S10>0,S11<0，则使an<0的最小的n的值是 （ ）
A．5 B．6 C．7 D．8
5．将函数y=f(x)·sinx的图象向右平移
个单位后，再作关于x轴的对称变换得到函数
y=－cos2x的图象.则f(x)可以是 （ ）
A．－2sinx B．2sinx C．－2cosx D．2cosx
6．已知
则x,y之间的大小关系是 （ ）
A．x>y B．x<y C．x=y D．不能确定
7．已知
、
为两个非零向量，有以下命题：①
=
，②·=，③、=且∥.其中可以作为=的必要但不充分条件的命题是 （ ）
A．② B．①③ C．②③ D．①②③
8．已知点
及抛物线
上一动点P（x,y）,则y+PQ的最小值是 （ ）
A．2 B．3 C．4 D．
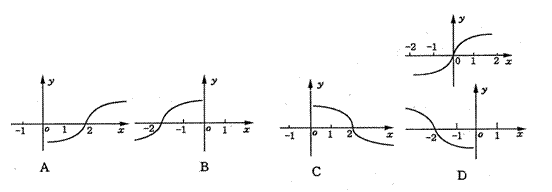9．方程f(x,y)=0的曲线如图所示，那么方程f(2－x,y)=0的曲线是 （ ）
10．抛物线y2=2x与过焦点的直线交于A、B两点，O是坐标原点，则
等于（ ）
A．－
B． C．－3 D．3
11．已知命题p：函数
的值域为R.命题q：函数
是减函数.若p或q为真命题，p且q为假命题，则实数a的取值范围是 （ ）
A．a≤1 B．a<2 C．1<a<2 D．a≤1或a≥2
12．对某地农村家庭拥有电器情况抽样调查如下：有电视机的占60%；有洗衣机的占55%；有电冰箱的占45%；至少有上述三种电器中的两种及两种以上的占55%；三种都有的占20%.那么没有任何一种电器的家庭占的比例是 （ ）
A．5% B．10% C．12% D．15%
第Ⅱ卷（非选择题，共90分）
二、填空题：（本大题4个小题，每小题4分，共16分）
13．△ABC中，若
的值为
.
14．把点A（2，1）按向量=（－2，3）平移到B，此时点B分向量
（O为坐标原点）的比为－2，则C点的坐标为
.
15．当x=3时，不等式
成立，则此不等式的解集是
.
16．奇函数f(x)的定义域为
值域为R，当且仅当x>1时，f(x)>0.关于f(x)有如下命题：①f(－1)=0；②方程f(x)=0有无穷解；③f(x)有最小值，但无最大值；④f(x)的图象关于原点对称，且f(x)是周期函数.其中正确命题的序号是
.
三、解答题：（本大题6个小题，共74分，必需写出必要的文字说明、推理过程或计算步骤.）
17．（12分）已知函数
（1）求f(x)的最大值与最小值；
（2）若
的值.
18．（12分）（1）已知=4，=3，（2－3）·（2+）=61，求与的夹角θ；
（2）设
=（2，5），
=（3，1），=（6，3），在上是否存在点M，使
，若存在，求出点M的坐标，若不存在，请说明理由.
19．（12分）定义在R上的函数f(x)满足f(x+2)=－f(x),且当x∈[－1，1]时，f(x)=x3.
（1）求f(x)在[1，5]上的表达式；
（2）若A={x
f(x)>a,x∈R},且A
，求实数a的取值范围.
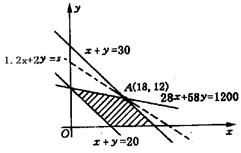
20．（12分）某集团准备兴办一所中学，投资1200万用于硬件建设.为了考虑社会效益和经济利益，对该地区教育市场进行调查，得出一组数据列表（以班为单位）如下：
| 班级学生数 | 配备教师数 | 硬件建设（万元） | 教师年薪（万元/人） | |
| 初中 | 60 | 2.0 | 28 | 1.2 |
| 高中 | 40 | 2.5 | 58 | 1.6 |
根据有关规定，除书本费、办公费外，初中生每年可收取学费600元，高中生每年可收取学费1500元.因生源和环境等条件限制，办学规模以20至30个班为宜.根据以上情况，请你合理规划办学规模使年利润最大，最大利润多少万元？
（利润=学费收入－年薪支出）
21．（12分）椭圆C1：
=1(a>b>0)的左右顶点分别为A、B.点P双曲线C2：
=1在第一象限内的图象上一点，直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.
（1）求P点的坐标；
（2）能否使直线CD过椭圆C1的右焦点，若能，求出此时双曲线C2的离心率，若不能，请说明理由.
22．（14分）已知
，若数列{an}
成等差数列.
（1）求{an}的通项an;
（2）设
若{bn}的前n项和是Sn，且
数学答案
一、选择题（本大题12个小题，每小题5分，共60分）
CBAB、DADA、CACD
二、填空题：（本大题4个小题，每小题4分，共16分）
13．
；14.（0,2）；15.
；16. ①②
三、解答题：（本大题6个小题，共74分）
17．（12分）
解：（1）由f(0)=2a=2, 得a=1 ,
…………（3分）
∴f(x)=2cos2x+2sinxcosx=sin2x+cos2x+1=
…………（5分）
∴f(x)的最大值是
，最小值是
.………………（6分）
（2）∵
.……（7分）
∴
…………（9分）
∴
………………（11分）
∴
.………………（12分）
18．（12分）解：（1）∵（2－3）·（2+）=61，∴
…（12分）
又=4，=3，∴·=－6.…………………………………………（4分）.
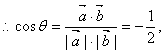………………………………………………（5分）
∴θ=120°.………………………………………………………………（6分）
（2）设存在点M，且
…………………………（8分）
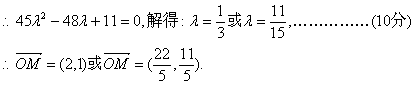
∴存在M（2，1）或
满足题意.……………………（12分）.
19．（12分）解：∵f(x+2)=-f(x), x∈R，∴f(x)= －f(x－2).……………（1分）
当x∈[1，3]时，x－2∈[－1,1],∴f(x)= －f(x－2)= －(x－2)3=(2－x)3.……（3分）
又f(x)= －f(x+2)=f(x+4), ∴f(x)是以4为周期的函数.………………（4分）
当x∈[3，5]时，x－4∈[－1,1], f(x)=f(x－4)= (x－4)3. ………………（6分）
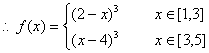…………………………………………（7分）
（2）当
当x∈[3,5]时，y= f(x)=(x－4)3, ∴y∈[－1,1],
∴f(x)在[1，5]上的值域为[－1,1].…………………………（9分）
又f(x)是以4为周期的函数，∴当x∈R时，f(x) ∈[－1,1]……（10分）
∴当a<1时，存在x使f(x)>a，故a的取值范围为a<1.………（12分）
20．（12分）
解：设初中x个班，高中y 个班，则
……………（4分）
设年利润为s，则
……（6分）
作出（1）、（2）表示的平面区域，如图，易知当直线1.2x+2y=s过点A时，s有最大值.
|
解得A（18，12）.……（10分）
（万元）.
即学校可规划初中18个班，高中12个班，
可获最大年利润为45.6万元.……（12分）
21．（12分）
解：（1）设P(x0,y0)(x0>a,y0>0)，又有点A(－a,0),B(a,0).
（2）
…………………………（7分）
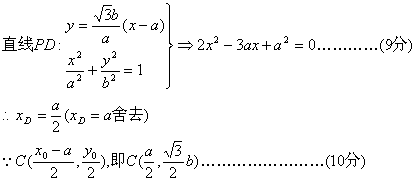
∴CD垂直于x轴.若CD过椭圆C1的右焦点，则
故可使CD过椭圆C1的右焦点，此时C2的离心率为
.…………（12分）
22．（14分）解：设2，f(a1), f(a2), f(a3),……，f(an),2n+4的公差为d，则
2n+4=2+(n+2－1)d
d=2,…………………………（2分）
……………………（4分）
（2）
，
