高三年第四次阶段考试数学试卷(文科)
命题人:林志森 审核人:郭远明
本卷满分150分, 考试时间120分钟.
考生须知:
1.在答题卷密封区内填写班级、姓名、号数和考号.
2.所有答案必须写在答题卡上, 写在试题卷上无效.
3.考试结束, 只需上交答题卡.
第I卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 直线l1: y=ax+1和l2: y =(2-a)x -1互相平行, 则a的值是( )
A.2 B.1 C.0 D.-1
2.在等差数列![]() 中,已知
中,已知![]() ,那么它的前8项和
,那么它的前8项和![]() 等于( )
等于( )
A.12 B.24 C.36 D.48
3.若a>b>c,则一定成立的不等式是 ( )
A.ac>bc B.ab>ac C.a![]() c>b
c>b![]() c D.
c D.![]()
4.函数![]() 的反函数是( )
的反函数是( )
A.y= (x-2)2+1 (x∈R) B.y= (x-2)2+1 (x≥2)
C.x= (y-2)2+1 (x∈R) D.y=(x-2)2+1 (x≥1)
5.已知焦点在y轴上的椭圆![]() 的离心率为
的离心率为![]() ,则m=( )
,则m=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知直线![]() 与圆
与圆![]() 相切,则直线l的倾斜角为( )
相切,则直线l的倾斜角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.函数![]() 在区间[-2,3]上的最大值与最小值分别是( )
在区间[-2,3]上的最大值与最小值分别是( )
A.5,4 B.13,4 C.68,4 D.68,5
9.圆![]() 轴交于A、B两点,圆心为P,若
轴交于A、B两点,圆心为P,若![]() ,
,
则实数c等于( )
A.1 B.-11 C.9 D.11
10.已知![]() =1,
=1,![]() =
=![]() ,且
,且![]() -
-![]() 与
与![]() 垂直,则
垂直,则![]() 与
与![]() 的夹角为( )
的夹角为( )
A.90° B.60° C.45° D. 30°
11.已知等比数列![]() 中,
中,![]() ,则
,则![]() ( )
( )
A.2 B.-5 C.2或-5 D.-2
12.已知P是椭圆![]() 上的点,Q、R分别是圆
上的点,Q、R分别是圆![]() 和圆
和圆![]() 上的点,则
上的点,则![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.10 D.9
C.10 D.9
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题;每小题4分,共16分.把答案写在答题卡的横线上)
13.已知过点P(2,-1)的直线与直线![]() :ax+y-b=0垂直,垂足为Q(-2,3),则
:ax+y-b=0垂直,垂足为Q(-2,3),则
a+b的值是____***__.
14.已知x、y满足约束条件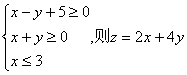 的最大值为 *** .
的最大值为 *** .
15. 已知![]() 是定义在R上的奇函数,则
是定义在R上的奇函数,则![]() 的值是_____*** .
的值是_____*** .
16.已知函数![]() 在区间[0,t]上至少取得2个最大值,则正整数t的最
在区间[0,t]上至少取得2个最大值,则正整数t的最
小值是 *** .
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)
17. (本题满分12分)已知函数![]() (
(![]() ,
,![]() 为常数),
为常数),
(Ⅰ)求![]() 的周期和单调递增区间;
的周期和单调递增区间;
(Ⅱ)若![]() 时,
时,![]() 的最小值为4,求
的最小值为4,求![]() 的值。
的值。
18. (本题满分12分) 记函数![]() 的定义域为
的定义域为![]() ,
,
![]() 的定义域为
的定义域为![]() ,
,
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 、
、![]() 的取值范围。
的取值范围。
19. (本题满分12分)已知直线l:y=-x+1与椭圆![]() =1(a>b>0)相交于A、B两点,且线段AB的中点为(
=1(a>b>0)相交于A、B两点,且线段AB的中点为(![]() ).
).
(1)求此椭圆的离心率;
(2)若椭圆的右焦点关于直线l的对称点在圆x![]() 上,求此椭圆的方程.
上,求此椭圆的方程.
20.已知等比数列![]() 公比q>1,且a1a2a3=27.
,a1+a2+a3=13,设数列
公比q>1,且a1a2a3=27.
,a1+a2+a3=13,设数列![]() 对任意的n∈N*,都有
对任意的n∈N*,都有![]() +
+![]() +
+![]() +┅+
+┅+![]() =
=![]() +1恒成立.
+1恒成立.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)求![]() ┅+
┅+![]() +
+![]() 的值.
的值.
21. (本题满分12分)一家服装公司生产某牌西装年固定成本为![]() 万元,每生产
万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足
,当年产量不足![]() 千件时,
千件时,![]() (万元);当年产量不小于
(万元);当年产量不小于![]() 千件时,
千件时,![]() (万元). 经过市场调查和测算,若每件售价为0.05万元时,该公司年内生产西装能全部销售完.
(万元). 经过市场调查和测算,若每件售价为0.05万元时,该公司年内生产西装能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一西装的生产中所获利润最大?
22. (本题满分14分)已知函数![]() ,且函数f(x)在x=1处取得极值,在x=2处的切线与向量
,且函数f(x)在x=1处取得极值,在x=2处的切线与向量![]() 平行.
平行.
(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)是否存在正整数m,使得方程![]() 内有且只
内有且只
有两个不等实根?若存在,求出m的值;若不存在,说明理由.
高三年第四次阶段考试数学试卷(文科)参考答案
一、选择题(本大题共12小题,每小题5分,共60分)
1—5.BDCBC 6—10.DCCBC 11—12.AD
二、填空题(本大题共4小题;每小题4分,共16分)
13. 4 14. 38 15. 2 16. 11
三、解答题(本大题共6小题,共74分)
17.解:(Ⅰ)∵![]() --------2′
--------2′
∴![]() -------3′
-------3′
由![]() ,得
,得![]() ---------5′
---------5′
∴单调递增区间为 ![]() ---------6′
---------6′
(Ⅱ)∵![]()
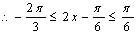 ---------8′
---------8′
![]() ---------10′
---------10′
当![]() 时,由
时,由![]()
![]() 得,
得,
![]() ---------12′
---------12′
18.解:(1)![]() ---------2分
---------2分
![]() ---------5分
---------5分
(2)![]() ---------6分
---------6分
由![]() ,得
,得![]() ---------8分
---------8分
则![]() ,即
,即![]() ---------10分
---------10分
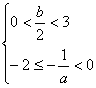
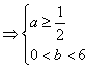 ---------12分
---------12分
19. 解:
(1)由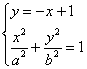 得 (b
得 (b![]() …1′
…1′
∵直线与椭圆相交两点
∴Δ=4a![]() >0
>0![]() a
a![]() >1 ……2′
>1 ……2′
设A(x![]() 则x
则x![]() ……3′
……3′
∵线段AB的中点为(![]() ∴
∴![]() ……4′
……4′
于是:a![]() ,又a
,又a![]() ∴a
∴a![]() ∴e=
∴e=![]() ……6′
……6′
(2)设椭圆的右焦点为F(c,0)
则点F关于直线l:y=-x+1的对称点P(1,1-c)……8′
由已知点P在圆x![]() , ∴1+(1-c)
, ∴1+(1-c)![]() =5 c
=5 c![]() -2c-3=0
-2c-3=0
∵c>0 ∴c=3, ……10′
从而a![]() =18,b
=18,b![]() =c
=c![]() =9
=9
所求的椭圆方程为:![]() ……12′
……12′
20解:(Ⅰ)由a1a2a3=27. ,a1+a2+a3=13, 得a2= 3. q=3(q>1)…3′
∴an=a2·qn-2=3·3 n-2=3 n-1 ……5′
![]() 对任意的n∈N*,有
对任意的n∈N*,有![]()
![]() +
+![]() +
+![]() +┅+
+┅+![]() =
=![]() +1 ①
+1 ①
∴当n=1时,![]() ,又
,又![]() ,∴
,∴![]() ; ………
6′
; ………
6′
当![]() 时,
时,![]() +
+![]() +
+![]() +┅+
+┅+![]() =
=![]() -1 ②
……7′
-1 ②
……7′
∴②-①得 ![]() ;
; ![]() ;……9′
;……9′
∴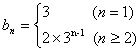 。 ……10′
。 ……10′
(Ⅱ) ![]()
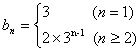
∴![]() ┅+
┅+![]() +
+![]()
=![]()
=![]() =
=![]() ……12′
……12′
21.解:(1)当![]() 时,
时,
![]()
……3′
当![]() ,
,![]() 时,
时,
![]()
…5′
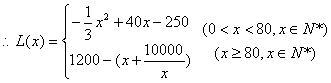
……6′
(2)当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ……8′
……8′
当![]()
![]()
![]()
当且仅当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值
![]() ……10′
……10′
综上所述,当![]() 时
时![]() 取得最大值
取得最大值![]() ,即年产量为
,即年产量为![]() 千件时,该公司在这一西装的生产中所获利润最大. ……12′
千件时,该公司在这一西装的生产中所获利润最大. ……12′
22.解:(1)由已知![]() .
.
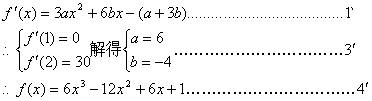
(2)![]()

(3)方程![]()
令g(x)=18x3-36x2+19……………9′

∴方程g(x)=0在区间(1,![]() ),(
),(![]() ,2)内分别有唯一实根…13′
,2)内分别有唯一实根…13′
∴存在正整数m=1使得方程![]() 在区间(1,2)上有且只有两个不相等的实数根.………………………14′
在区间(1,2)上有且只有两个不相等的实数根.………………………14′