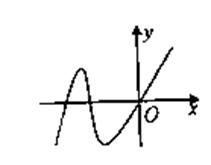高三年级毕业班联考数学(文)试题
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试时间120分钟。考试结束后,将Ⅱ卷和答题卡一并交回。
第Ⅰ卷(选择题,共50分)
注意事项:
1.答第Ⅰ卷前,考生力必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.选出答案后,用铅笔把答题卡上对应的题目的答案标号涂黑,如需改动,用橡皮擦
干净后,再填涂其它答案,不能答在试题卷上。
参考公式:
如果事件A、B互斥,那么 P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P.
那么n次独立重复试验中恰好发生k次的概率![]()
一、选择题:(本题共10个小题,每小题5分,共50分。在每小题给出的四个选项中,有且只有一个是正确的,把正确答案涂在答题卡上)
1.设集合![]() 等于
等于
( )
![]() A.
A.![]() B.R
B.R
C.{0} D.
2.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.若![]() 表示双曲线”的 ( )
表示双曲线”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.即不充分也不必要条件
4.某单位邀请10位教师中的6位参加一个会议,其中甲、乙两位教师不能同时参加,则邀
请的不同方法有 ( )
A.84种 B.98种 C.112种 D.140种
5.设正数x,y满足![]() 的最大值是 ( )
的最大值是 ( )
A.1 B.2 C.4 D.10
6.把直线![]() 平移后,所得直线与圆
平移后,所得直线与圆![]()
相切,则则实数P的值为 ( )
A.-39 B.-21 C.13 D.39
7.若![]() 的展开式中含x的项为第6项,设
的展开式中含x的项为第6项,设![]() 则
则
![]() 的值为 ( )
的值为 ( )
A.-225 B.-32 C.32 D.255
8.已知偶函数![]() 则方程
则方程
![]() 的解的个数为 ( )
的解的个数为 ( )
A.6 B.7 C.12 D.14
9.等差数列![]() 等于( )
等于( )
A.—1221 B.—21.5 C.—20.5 D.—20
|
的图象如图,则![]() 的值 ( )
的值 ( )
A.大于0
B.小于0
C.等于0
D.以上都有可能
第Ⅱ卷(非选择题,共100分)
注意事项:
| |
2.答卷前,请将密封线内的项目填写清楚。
二、填空题:本大题共6小题,每小题4分,共24分,把答案填答题卷中相应的横线上。
11.曲线![]() 关于直线y=1对称的曲线的普通方程是
.
关于直线y=1对称的曲线的普通方程是
.
12.在一批产品中,有n件一级品,36件二级品,60件三级品,现按分层抽样的方法抽出的20件样品中,有10件三级品,则n= .
13.已知![]() .
.
14.在![]() 角A、B、C所对的边分别为a,b,c已知A=60°,b=1,c=4,则sinB的值等于
.
角A、B、C所对的边分别为a,b,c已知A=60°,b=1,c=4,则sinB的值等于
.
15.以椭圆![]() 一条渐近线为y=2x的双曲线的方程
.
一条渐近线为y=2x的双曲线的方程
.
16.关于函数![]() ,有下列命题:
,有下列命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ,其图像的一个对称中心是
,其图像的一个对称中心是![]() ;
;
②函数![]() 的最小值是
的最小值是![]()
③函数![]() 的图象按向量
的图象按向量![]() 平移后所得的函数是偶函数;
平移后所得的函数是偶函数;
④函数![]() 在区间
在区间![]() 上是减函数
上是减函数
其中所有正确命题的序号是 .
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤
17.(本题满分12分)已知A、B、C为![]() 的三个内角,
的三个内角,![]()
![]()
(Ⅰ)若![]() 求角A;
求角A;
(Ⅱ)若![]() ,求tan2A.
,求tan2A.
18.(本小题满分12分)已知函数![]() 的图象关原点对称,
的图象关原点对称,![]() 的图象在点P(1,m)处的切线的斜率为-6,且当x=2时
的图象在点P(1,m)处的切线的斜率为-6,且当x=2时![]() 有极值.
有极值.
(Ⅰ)求a,b,c,d的值
(Ⅱ)若![]() 在区间
在区间![]() 上是增函数,求n的取值范围.
上是增函数,求n的取值范围.
19.(本小题满分12分)在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一巨大汽没罐,已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是![]() ,每次命中与否互相独立.
,每次命中与否互相独立.
(Ⅰ)直到第三次射击汽油才流出的概率;
(Ⅱ)直到第三次射击油罐才被引爆的概率;
(Ⅲ)求油罐被引爆的概率.
20.(本题满分12分)已知函数![]()
| |
(Ⅱ)点![]() 在区域D运动时,求关于x,y的式子
在区域D运动时,求关于x,y的式子![]() 的最大值.
的最大值.
|
21.已知数列![]()
求:
(Ⅰ)数列![]() 的通项公式;
的通项公式;
(Ⅱ)数列![]() 前n项和Sn.
前n项和Sn.
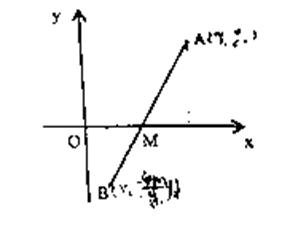
22.(本小题满分14分)如图,线段AB过点M(m,0),m为正数,且点A、B到x轴的距离之积为4m,抛物线C以x轴为对称轴,且过O、A、B三点(其中O为坐标原点).
(Ⅰ)求抛物线C的方程;
|
高三年级毕业班联考数学(文)试题参考答案
一、选择题:(本题共10个小题,每小题5分,共50分。)
ADAD BBDC CA
二、填空题:本大题共6小题,每小题4分,共24分
11.![]()
12.24
13.2
14.![]()
15.![]()
16.①②③
三、解答题:本大题共6小题,共74分
17.解:
(Ⅰ)由已知![]()
化简得![]() (3分)
(3分)
![]()
![]() (5分)
(5分)
(Ⅱ)![]()
![]() ①,
①,
平方得![]()
![]()
![]() ②(7分)
②(7分)
联立①、②得,![]()
![]() (10分)
(10分)
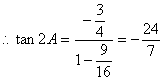 (12分)
(12分)
18.解:
(Ⅰ)![]() ………………2分
………………2分
由条件可得![]() ………………4分
………………4分
![]()
故![]() ………………6分
………………6分
(Ⅱ)![]()
![]() ………………8分
………………8分
令![]()
![]() ;………………10分
;………………10分
![]() 上是增函数
上是增函数
![]()
即![]() ………………12分
………………12分
19.解:
(Ⅰ)第三次射击汽油才流出的概率
![]() ………………3分
………………3分
(Ⅱ)第三次射击被引爆的概率
![]() ………………7分
………………7分
(Ⅲ)“油罐被引的事件为事件A,其对立事件为![]() ”则
”则
|
![]() ………………12分
………………12分
20.解:
(Ⅰ)![]()
![]() ………………2分
………………2分
由题意得![]() ………………3分
………………3分
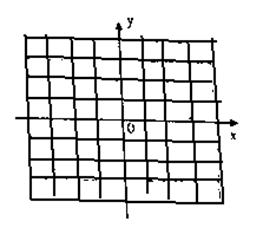
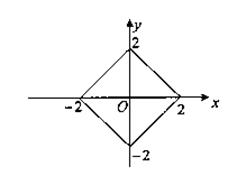
平面区域D(如图正方形内部区域及边界)………………5分
平面区域D的面积为8………………7分
(Ⅱ)![]()
(其中d是D中的点(x,y)到直线![]() 的距离)………………10分
的距离)………………10分
由(Ⅰ)图可知d的最大值为(0,2)点到直线![]() 的距离
的距离
即所求最大值为![]() ………………12分
………………12分
注:本题也可以以先求![]() 的范围[-20,-4],再得结果,请参照给分.
的范围[-20,-4],再得结果,请参照给分.
21.解:
(Ⅰ)![]() (1)
(1)
![]() (2)…2分
(2)…2分
由(1)—(2)得![]() (3)…………5分
(3)…………5分
在(1)中令![]() (3)式,故
(3)式,故![]() ………………6分
………………6分
(Ⅱ)设![]() 其前n项和为
其前n项和为![]() 则
则
![]() (4)………………7分
(4)………………7分
![]() (5)………………8分
(5)………………8分
由(5)—(4)得![]() ………………10分
………………10分
![]() ………………12分
………………12分
![]() ………………14分
………………14分
22.(本小题分14分)
解:(Ⅰ)设抛物线![]() (1分)
(1分)
若k存在,设直线AB的方程为![]() (2分)
(2分)
并设点![]()
由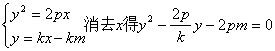 (3分)
(3分)
![]() (5分)
(5分)
![]() (6分)
(6分)
![]()
![]() (7分)
(7分)
若k不存在,知抛物线C过点![]()
![]()
![]() (8分)
(8分)
故所求抛物线C的方程为![]() (9分)
(9分)
(Ⅱ)由(Ⅰ)得![]()
![]()
![]() (10分)
(10分)
又![]()
![]()
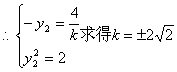 (13分)
(13分)
![]() (14分)
(14分)