高三第二次摸底考试模拟题数学卷
总分150分
一、选择题：
1. 已知角
的终边过点P（－8m, －6sin30°），且cos
，则m的值为（ ）
A．
B．
C． 
D． 
2. 给定两个向量
的值等于（ ）
A．－3 B．
C．3 D．
3. 若互不相等的实数a、b、c成等差数列, c、a、b成等比数列，且a＋3b＋c＝10, 则a等于（ ）
A．4 B．－2 C．2或－4 D．－4
4．已知命题p：函数
的值域为R，命题q：函数
是减函数。若p或q为真命题，p且q为假命题，则实数a的取值范围是（ ）
A．a
1 B．1<a<2 C．a<2 D．a1或a
2
5．直线
的方向向量为
，直线的倾角为
，则
（ ）
A. 
B. 
C.
D. 
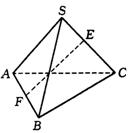
6．如图，在正四面体S-ABC中，E、F分别是SC、AB的中点，则直线EF与SA所成的角为（ ）．
A．90° B．60° C．45° D．30°
7. 椭圆
（a>b>0）的两焦点为F1、F2，连接点F1，F2为边作正三角形，若椭圆恰好平分正三角形的另两条边，则椭圆的离心率为（ ）
A．
B．
C．
D．
8. 设函数
是定义在R上的以5为周期的奇函数，若
，则a的取值范围是（ ）
A．
B．
C．
D．
9．已知l,m,表示直线，
表示平面，下列条件中能推出结论的正确的是：条件：
①l⊥m, l⊥, m⊥
; ②∥, ∥
; ③l⊥, ∥;④ l⊥, m⊥
结论：a:
l ⊥
b: ⊥ c: l∥m d: ∥
A ①
a,②b,③c,④d B ①b,②d,③a,④c
C ①c,②d,③a,④b D ①d,②b,③a,④c
10. 一束光线从点A(－1, 1)出发经x轴反射，到达圆C：(x－2)2＋(y－3)2=1上一点的最短路程是（ ）。
A．4 B．5
C．3
－1 D．2
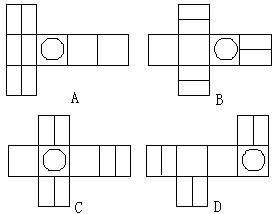
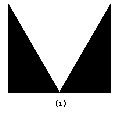
11. 正方体的直观图如右图所示，则其展开图是 （ ）
12．已知
的非等腰三角形，且
，则关于x的二次方程
的根的个数叙述正确的是（ ）
A．无实根 B．有两相等实根 C．有两不等实根 D．无法确定
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分.
13．
在直线上的射影为
，则直线的方程是 。
14．2005年10月27日全国人大通过关于修改个人所得税法的决定，个税起征点从800元提高到1600元，也即是说原来月收入超过800元部分就要纳税，2006年1月1日起月收入超过1600元需纳税，若税法修改前后超过部分的税率相同，如下表
| 级数 | 全月应纳税所得额 | 税率（%） |
| 1 | 少于500元 | 5 |
| 2 | 500～2000元 | 10 |
| 3 | 2000～5000元 | 15 |
某人2005年3月交纳个人所得税123元，则按新税法此人少交纳 元。
15．数列{an}、{bn}都是等差数列,a1=0、b1= -4,用Sk、Sk′分别表示{an}、{bn}的前k项和(k是正整数),若Sk+ Sk′=0,则ak+bk= 。
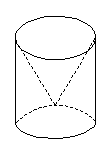
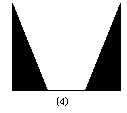
16．如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得到的，现用一个平面去截这个几何体，若这个平面垂直于圆柱底面所在的平面，那么所截得的图形可能是图中的_________.（把所有可能的图的序号都填上）
 | |||||||||
 | |||||||||
 | |||||||||
 |  | ||||||||
绝密★★★启用前
三、解答题：
17．（本小题满分12分）在△ABC中，角A、B、C所对的边分别是a、b、c，若
，且
，求△ABC的面积
18. （本小题满分12分）已知
为实数，求使
成立的x的范围.
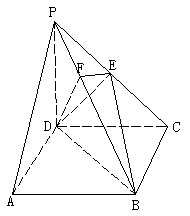
19．（本小题满分12分）如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F。
（1）证明PA//平面EDB；
（2）证明PB⊥平面EFD；
（3）求二面角C—PB—D的大小。（只要求理科学生做）
20. (本小题满分12分) 设x=1与x=2是函数f(x) = a lnx + bx2 + x的两个极值点.
（Ⅰ）试确定常数a和b的值；
（Ⅱ）试判断x=1，x=2是函数f(x)的极大值还是极小值，并说明理由.
21. (本小题满分12分)已知直线
与椭圆
相交于A、B两点，且线段AB的中点在直线
上.
（Ⅰ）求此椭圆的离心率；
（Ⅱ）若椭圆的右焦点关于直线的对称点的在圆
上，求此椭圆的方程.
22．（本小题满分14分）设数列
的各项都是正数，且对任意
，都有
，记
为数列的前n项和。
（1）求证：
；
（2）求数列的通项公式；
（3）（要求：理科学生必做；文科学生选做）
若
（
为非零常数，），问是否存在整数，使得对任意，都有
。
高三第二次摸底考试模拟题数学卷答案
一、选择题答案：
1—5 C A D B C 6--10 C D A B A 11--12 D C
二、填空题答案：
13．
； 14．80 ； 15．4； 16． （1）（3）
三、解答题：
17．解：由已知得b2+c2=a2+bc……………………………2分
………………………4分
………………………………6分
由
…………10分
………………………………12分
18. 解：
………2分
10当m=0时，x＞1…………………4分
20当m≠0时，
①m＜0时，
…………………6分
②0＜m＜1时，
………………8分
③m=1时， x 不存在………………………10分
④m＞1时，
……………………………12分
19． 解（1）证明：连结AC，AC交BD于O，连结EO。
∵底面ABCD是正方形，∴点O是AC的中点
在
中，EO是中位线，∴PA // EO………………理2分、文3分
而
平面EDB且
平面EDB，
所以，PA // 平面EDB…………………………理4分、文6分
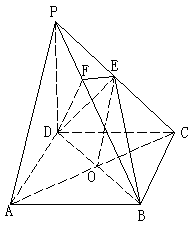
（2）证明：
∵PD⊥底面ABCD且
底面ABCD，∴
∵PD=DC，可知
是等腰直角三角形，而DE是斜边PC的中线，
∴
。 ①………………………理6分、文8分
同样由PD⊥底面ABCD，得PD⊥BC。
∵底面ABCD是正方形，有DC⊥BC，∴BC⊥平面PDC。
而
平面PDC，∴
。 ②
由①和②推得
平面PBC。………………理7分、文10分
而
平面PBC，∴
又
且
，所以PB⊥平面EFD。……理8分、文12分
（3）解：由（2）知，
，
故
是二面角C—PB—D的平面角。………………理9分
由（2）知，
。
设正方形ABCD的边长为a，则
， 
。
在
中，
。
在
中，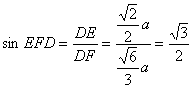
，∴
。
所以，二面角C—PB—D的大小为
。………………理12分
20．解：（Ⅰ）f′(x)=
+2bx+1………………2分
由极值点的必要条件可知：f′(1)=f′(2)=0,
即a+2b+1=0, 且
+4b+1=0, ………………4分
解方程组可得a=－
,b=－
,
∴f(x)=－lnx－x2+x ………………7分
（Ⅱ）f′(x)=－x-1－
x+1, ………………8分
当x∈(0,1)时，f′(x)＜0,
当x∈(1,2)时，f′(x)＞0,
当x∈(2,+∞)时，f′(x)＜0, ………………10分
故在x=1处函数f(x)取得极小值
,………………11分
在x=2处函数取得极大值
－ln2. ………………12分
21． 解:（1）设A、B两点的坐标分别为
得
, …………………………3分
根据韦达定理，得
∴线段AB的中点坐标为（
）. ………………5分
由已知得
故椭圆的离心率为
. …………………………7分
（2）由（1）知
从而椭圆的右焦点坐标为
设
关于直线的对称点为
解得 
…………………………10分
由已知得 
故所求的椭圆方程为
. …………………………12分
22．解（1）在已知式中，当
时，
∵ 
∴ 
………………………理1分、文2分
当
时， ①
②
①－②得，
……………理3分、文5分
∵ 
∴ 
，
即∵ 适合上式
∴ 
………………理5分、文7分
（2）由（1）知， ③
当时，
④
③－④得
∵ 
∴ 
………理8分、文12分
∴ 数列是等差数列，首项为1，公差为1，可得
…………………………理9分、文14分
（3）∵ ∴ 
∴ 
∴ 
⑤………………理11分
当
，
，2，3，…时，⑤式即为
⑥
依题意，⑥式对
…都成立，∴ 
………………理12分
当
，
…时，⑤式即为
⑦
依题意，⑦式对…都成立，∴ 
……………理13分
∴ 
，又
∴ 存在整数
，使得对任意
，都有…………理14分