高三第二次模拟考试数学试题(理)
时间120分钟 总分150分 命题人:曹干铁 审校人:王立象等
第Ⅰ卷(选择题共50分)
参考公式:
如果事件![]() 、
、![]() 互斥,那么
互斥,那么![]()
如果事件![]() 、
、![]() 相互独立,那么
相互独立,那么![]() ·
·![]() ·
·![]()
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么它在
,那么它在![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]()
球的表面积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
球的体积公式![]() ,其中
,其中![]() 表示球的半径.
表示球的半径.
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知函数![]() ,它的反函数为
,它的反函数为![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
2.公差不为零的等差数列![]() 中,
中,![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列,则数列
成等比数列,则数列![]() 的公差等于
的公差等于
A . 4 B. 3 C. 2 D. 1
3.已知平面![]() ,直线
,直线![]() ,点
,点![]() ,有下面四个命题:
,有下面四个命题:
①若![]() ,则
,则![]() 与
与![]() 必为异面直线;
必为异面直线;
②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ;
;
④若![]() ,则
,则![]() 。
。
其中正确命题的个数是( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设![]() 是集合A到B的映射,如果
是集合A到B的映射,如果![]() ,则
,则![]() 等于
等于
A .
![]() B.
B.
![]() C.
C.
![]() 或
或![]() D.
D.![]() 或
或![]()
5.若条件p:![]() ,条件q:2<x<3,则
,条件q:2<x<3,则![]() 是
是![]() 的
的
A.必要不充分条件;B.充分不必要条件;C.充要条件;D.既非充分也非必要条件
6.在![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是角A,B,C所对的边,
分别是角A,B,C所对的边,![]() ,
,![]() ,
,![]() 的面积
的面积![]() ,则
,则![]() 的值等于
的值等于
A.![]() .
B.
.
B. ![]() C.
C.![]() D.
D.![]()
7.从6人中选出4人分别到莽山、韶山、衡山、张家界4个旅游景点游览,要求每个景点
有一人游览,每人只游览一个景点,且这6人中甲、乙两人不去莽山景点游览,则不同的选
择方案共有
 A.300种 B.240种 C.144种 D.96种
A.300种 B.240种 C.144种 D.96种
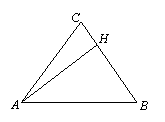
8.如图:在△ABC中,![]() ,
,![]() ,则过点C,以A、H为两焦点的双曲线的离心率为( )
,则过点C,以A、H为两焦点的双曲线的离心率为( )
A. B. C.2 D.3
9.平面上有相异的11个点,每两点连成一条直线,共得48条直线,则任取其中的三个点,构成三角形的概率是
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
10.一次研究性课堂上,老师给出一个函数![]() ,四位同学甲、乙、丙、丁在研究此函数时各给出了一个命题:
,四位同学甲、乙、丙、丁在研究此函数时各给出了一个命题:
(1)甲:函数![]() 的值域为
的值域为![]()
(2)乙:若![]() ,则有
,则有![]()
(3)丙:关于![]() 的方程
的方程![]() (
(![]() 为常数且
为常数且![]() )的所有实数解的和与
)的所有实数解的和与![]() 有关
有关
(4)丁:若规定![]() ,
,![]() ,则
,则![]() 对任意
对任意![]() 恒成立上述四个命题正确的有
恒成立上述四个命题正确的有
A. 1 个 B. 2个 C. 3个 D. 4个
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡中对应题号后的横线上.
11.已知圆![]() 与抛物线y2=2px(p>0)的准线相切,则p=
与抛物线y2=2px(p>0)的准线相切,则p=
12.若![]() 的展开式中的第五项等于 , 则
的展开式中的第五项等于 , 则![]() =
=
13.某学校对学生身高进行统计. 所有学生的身高数近似服从正态分布![]() ,已知所有学生中身高在153cm以下的人数为202人,则该校学生总人数约为
,已知所有学生中身高在153cm以下的人数为202人,则该校学生总人数约为
人(用整数作答).
以下供查阅的部分标准正态分布数据可选择使用:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 14.正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,若图中三角形(正四面体的截面)的面积是
14.正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,若图中三角形(正四面体的截面)的面积是![]() ,则该球球面面积为
,则该球球面面积为
15.设![]() 为坐标原点,
为坐标原点,![]() ,若
,若![]() 的坐标满足
的坐标满足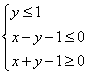 ,则
,则![]() 的最大值是
的最大值是
三、解答题:本大题共6小题,共75分. 解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)已知向量 ![]() ,
,![]() ,
,![]() ,函数
,函数 ![]() ,
, ![]() .
.
(1)要得到![]() 的图象,只需把
的图象,只需把![]() 的图象经过怎样的平移或伸缩变换?
的图象经过怎样的平移或伸缩变换?
(2)求![]() 的最大值及相应的x.
的最大值及相应的x.
17.(本小题满分12分)10个实习小组在显微镜下试测一块矩形芯片,测得其长为![]() 的小组分别有3个,5个,2个,测得其宽为
的小组分别有3个,5个,2个,测得其宽为![]()
![]()
![]() 的小组分别有3个,4个,3个,设测量中矩形芯片的长与宽分别为随机变量
的小组分别有3个,4个,3个,设测量中矩形芯片的长与宽分别为随机变量![]() 和
和![]() ,周长为
,周长为![]() 。
。
⑴分别写出随机变量![]() 和
和![]() 的分布列;
的分布列;
⑵求周长![]() 的分布列及
的分布列及![]() 的数学期望。
的数学期望。
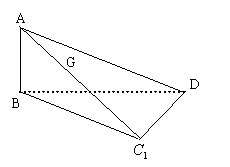
18.(本小题满分12分)如图,在平行四边形ABCD中,![]() ,将它们沿对角线
,将它们沿对角线![]() 折起,折起后C变为
折起,折起后C变为![]() ,且
,且![]() 、
、![]() 间的距离为2
间的距离为2
 (1)求证:平面
(1)求证:平面![]()
![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)![]() 为线段
为线段![]() 上的一个动点,当线段
上的一个动点,当线段![]() 的长为多少时,
的长为多少时,![]() 与平面
与平面![]() 成的角为
成的角为![]() .
.
19、(本小题满分12分)某市拟在半径为![]() 的圆形花园中心竖建一高杆顶灯,若地面各点的亮度与光线和地面所成角的正弦值成正比,与该点到灯的距离的平方成反比。
的圆形花园中心竖建一高杆顶灯,若地面各点的亮度与光线和地面所成角的正弦值成正比,与该点到灯的距离的平方成反比。
(1) 问高杆顶灯的灯柱设计为多高时,沿花园周边小路上的亮度最大?
(2) 小路上亮度最大时,用你所学的数学知识说明花园内各点的亮度与这点到高杆顶灯底部(花园中心)距离的变化关系。
20.(本小题满分13分)在数列{an}中,a1=![]() ,an+1=
,an+1= ![]() (n∈N*)
(n∈N*)
(1)证明:an>2(n∈N*);
(2)对于n∈N*证明:
①an+1-2<![]() (an-2);
(an-2);
②a1+a2+a3+…+an<2n+1.
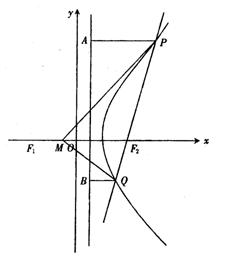
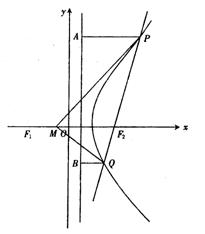
21.(本小题满分14分)已知![]() 満足:
満足:![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 过点
过点![]() 且与轨迹
且与轨迹![]() 交于
交于![]() 、
、![]() 两点.
两点.
(i)无论直线![]() 绕点
绕点![]() 怎样转动,在x轴上总存在定点
怎样转动,在x轴上总存在定点![]() ,使
,使![]() 恒成
恒成
立,求实数![]() 的值.
的值.
(ii)过![]() 、
、![]() 作直线
作直线![]() 的垂线
的垂线![]() 、
、![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,记
,记![]() ,求λ的取值范围.
,求λ的取值范围.
高三第二次模拟考试数学试题(理)参考解答(理)
1.B. 2.C.3.B.4.D.5、A、6.A、7.B. 8.C. 9.D、10.C.
11.2;12. 1 ;13.2500.; 14.![]() ; 15.
; 15.
![]()
16、解:(1)![]() =
=![]() =
= ![]()
=![]() =
=![]() …………………………………2分
…………………………………2分
![]() =
=![]() =
=![]() ……………4分
……………4分
所以要得到![]() 的图象只需把
的图象只需把![]() 的图象向左平移
的图象向左平移![]() 即可.……6分
即可.……6分
(2)![]() =
= ![]() -
-![]()
=![]() -
-![]()
=![]() ………………………………………………9分
………………………………………………9分
当![]() ,即
,即![]()
![]() 时,
时,
![]() 取得最大值
取得最大值![]() …………………………………………………12分
…………………………………………………12分
17.解:⑴随机变量![]() 的分布律如下表:
的分布律如下表:
| 长度 | 29 | 30 | 31 |
| P | 0.3 | 0.5 | 0.2 |
| 宽度 | 19 | 20 | 21 |
| P | 0.3 | 0.4 | 0.3 |
……………………………………………………………………………4分
⑵解法一(利用周长的分布计算)
![]()
![]()
![]()
![]()
![]() ,周长分布律如下表:
,周长分布律如下表:
| 周长 | 96 | 98 | 100 | 102 | 104 |
| P | 0.09 | 0.27 | 0.35 | 0.23 | 0.06 |
……………………………………………………………………………9分
![]()
………………………………………12分
解法二:由长和宽的分布率可得
![]()
![]()
由期望的性质可得![]() ……………………………12分
……………………………12分
18.解法一:(1)![]() ABCD为平行四边形
ABCD为平行四边形
![]()
![]()
即![]()
![]() ;………………………………………………1分
;………………………………………………1分
在![]() 中,
中,![]() ,
,![]()
又![]()
![]()
![]()
![]() ………………………………………………………3分
………………………………………………………3分
![]() 平面
平面![]()
又![]() 平面
平面![]()
![]()
![]() ;………………………………………………4分
;………………………………………………4分
(2)由(1)知![]()
![]() ;
;
![]()
![]()
过![]() 作
作![]() 于
于![]()
则![]()
![]()
过![]() 作
作![]() 于
于![]()
连![]()
由三垂线定理的逆定理知![]()
![]() 为二面角
为二面角![]() 的平面角………………………………………………6分
的平面角………………………………………………6分
由![]() ,
,![]()
有![]()
![]()
在![]() 中,
中,![]()
![]()
在![]() 中,
中,![]()
![]()
在![]() 中,
中, ![]()
![]() 二面角
二面角![]() 的大小是为
的大小是为![]() …………………………………………8分
…………………………………………8分
(3)猜想![]() 为
为![]() 的中点时,
的中点时,![]() 与平面
与平面![]() 成的角为
成的角为![]()
 证明(略)
………………………………………………………12分
证明(略)
………………………………………………………12分
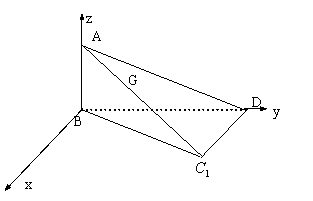
解法二:(1)同解法一
(2)由(1)易知![]() 平面
平面![]()
建立如图所示空间直角坐标系,则
![]()
![]()
![]()
![]()
![]()
![]()
![]()
设平面![]() 的法向量为
的法向量为![]()
由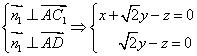
可取![]()
设平面![]() 的法向量为
的法向量为![]()
由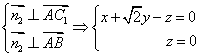
可取![]()
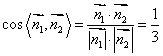
又可知二面角![]() 是锐角.
是锐角.
∴二面角![]() 的大小是
的大小是![]() .………………………………………8分
.………………………………………8分
(3)令![]()
则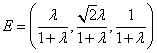
从而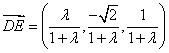
易知平面![]() 的法向量为
的法向量为![]()
则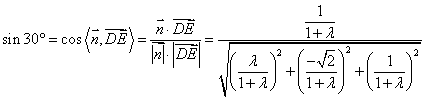
![]()
因此当线段![]() 的长为1时,
的长为1时,![]() 与平面
与平面![]() 成的角为
成的角为![]() .…………………………12分19、(1)解:设高杆顶灯的柱高为
.…………………………12分19、(1)解:设高杆顶灯的柱高为![]() (即顶灯到地面的距离为
(即顶灯到地面的距离为![]() ),光线和地面所成角
),光线和地面所成角![]() ,花园周边小路上的亮度为
,花园周边小路上的亮度为![]() ,依题意有
,依题意有
![]() …………………………………………………………………………2分
…………………………………………………………………………2分
又![]() …………………………………………………………………………3分
…………………………………………………………………………3分
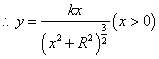 ……………………………………………………………………4分
……………………………………………………………………4分
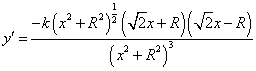 …………………………………………………5分
…………………………………………………5分
当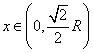 时,
时,![]()
当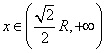 时,
时,![]() …………………………………………………………6分
…………………………………………………………6分
所以,当且仅当![]() 时,
时,![]() 取得最大值
取得最大值
即高杆顶灯的顶灯的柱高为![]() 时,花园周边小路上的亮度最大…………………7分
时,花园周边小路上的亮度最大…………………7分
(2)当高杆顶灯的柱高为![]() 时,设花园内一点与花园中心(灯底)的距离为
时,设花园内一点与花园中心(灯底)的距离为![]() 。由(1)知该点的亮度为
。由(1)知该点的亮度为
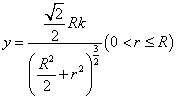 ……………………………………………………………9分
……………………………………………………………9分
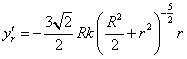 …………………………………………………………10分
…………………………………………………………10分
![]() ,
,![]()
![]()
从而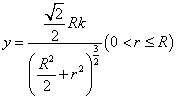 是关于
是关于![]() 的减函数,………………………………11分
的减函数,………………………………11分
即离花园中心越远的点,亮度越小 ……………………………………………………12分
20.证明:(1)①当n=1时,a1=![]() 结论成立
结论成立
②假设当n=k时,不等式ak>2成立
当n=k+1时,ak+1=![]()
ak+1-2=![]() -2=
-2=![]() >0
>0
∴ak+1>2,即当n=k+1时,不等式也成立………………………………………5分
由(1)(2)知,an>2对n∈N*都成立.
(2)①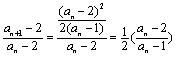 ……………………………………7分
……………………………………7分
∵0<![]() <1
<1
∴![]()
即an+1-2<![]() (an-2). …………………………………………………………9分
(an-2). …………………………………………………………9分
②由①an-2<(an-1-2)<![]() (an-2-2)<…<
(an-2-2)<…<![]() (a1-2)=
(a1-2)=![]()
∴an<2+![]() …………………………………………………………11分
…………………………………………………………11分
∴a1+a2+a3+…+an<(2+![]() )+(2+
)+(2+![]() )+…+(2+
)+…+(2+![]() )
)
=2n+(![]() +
+![]() +…+
+…+![]() )
)
=2n+1-![]() <2n+1. …………………………………………13分
<2n+1. …………………………………………13分
21.解:(1)![]() 由
由![]()
得![]() ,点P的轨迹E是以F1、F2为焦点的双曲线右支,由
,点P的轨迹E是以F1、F2为焦点的双曲线右支,由![]() ,故轨迹E的方程为
,故轨迹E的方程为![]() …………4分
…………4分
(2)当直线l的斜率存在时,设直线方程为![]() ,与双曲线方程联立消y得
,与双曲线方程联立消y得![]() ,
,
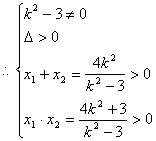
解得k2 >3 ………………………………………………………………………………5分
(i)![]()
|
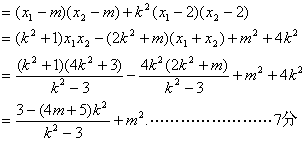
![]() ,
,
故得![]() 对任意的
对任意的
![]() 恒成立,
恒成立,
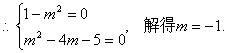
∴当m =-1时,MP⊥MQ.
当直线l的斜率不存在时,由![]() 知结论也成立,
知结论也成立,
综上,当m =-1时,MP⊥MQ. ……………………………………………………8分
(ii)![]() 是双曲线的右准线,……………………………9分
是双曲线的右准线,……………………………9分
由双曲线定义得:![]() ,
,
方法一: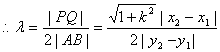
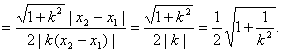 ………10分
………10分
![]() ,…………………………………………12分
,…………………………………………12分
注意到直线的斜率不存在时,![]() ,
,
综上,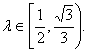 ………………………………………………………………14分
………………………………………………………………14分
方法二:设直线PQ的倾斜角为θ,由于直线PQ与双曲线右支有二个交点,
![]() ,过Q作QC⊥PA,垂足为C,则
,过Q作QC⊥PA,垂足为C,则
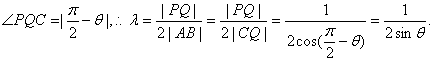 ………12分
………12分
|
故: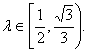 ………………14分
………………14分