高三第二次五校联考数学(文科)试题
参考公式:
如果事件 A , B 互斥,那么P( A+ B )= P( A)+ P(
B) , P( A+ B)= P(
A)![]() P( B)
P( B)
如果事件A在一次试验中发生的概念是p,那么n次独立重复试验中恰好发生 k次的概率:![]()
球的表面积公式:S=![]() , 其中 R 表示球的半径
, 其中 R 表示球的半径
球的体积公式V=![]() ,其中R表示球的半径
,其中R表示球的半径
卷一
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知四边形ABCD上任意一点P在映射![]() :
:![]() →
→![]() 作用下的象P‘构成的图形为四边形
作用下的象P‘构成的图形为四边形![]() 。若四边形ABCD的面积等于6,则四边形
。若四边形ABCD的面积等于6,则四边形![]() 的面积等于 ( )
的面积等于 ( )
A.9 B.![]() C.
C.![]() D.6
D.6
2.方程![]() 的根所在的区间是 ( )
的根所在的区间是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
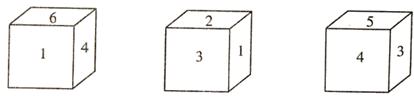
3.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记3的对面的数字为m,4的对面的数字为n,那么m+n的值为( )
|
4.以下通项公式中,不是数列![]() 的通项公式的是 ( )
的通项公式的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.有一种波,其波形为函数![]() 的图象,若其在区间[0,
的图象,若其在区间[0,![]() ]上至少有2个波峰(图象的最高点),则正整数
]上至少有2个波峰(图象的最高点),则正整数![]() 的最小值是 ( )
的最小值是 ( )
A.5 B.6 C.7 D.8
6.已知集合A中有10个元素,B中有6个元素,全集U中有18个元素,设∁U(A∪B)有x个元素,则x的取值范围是 ( )
A.3≤x≤8且x∈N B.2≤x≤8且x∈N
C.8≤x≤12且x∈N D.10≤x≤15且x∈N
7.已知平面向量![]() ,则
,则![]() 的值为
的值为
( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
8.要从10名女生与5名男生中选取6名学生组成课外兴趣小组,如果按性别分层随机抽样,则能组成课外兴趣小组的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知直线![]() 通过抛物线
通过抛物线![]() 的焦点
的焦点![]() ,且与抛物线相交于
,且与抛物线相交于![]() 两点,分别过
两点,分别过![]() 两点的抛物线的两条切线相交于
两点的抛物线的两条切线相交于![]() 点,则
点,则![]() 的大小是 ( )
的大小是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设![]() 是异面直线,给出下列四个命题:①存在平面
是异面直线,给出下列四个命题:①存在平面![]() ,使
,使![]() ;
;
|
其中正确命题的个数有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题:本大题共7小题,每小题4分,共28分。
11.原点和点![]() 在直线
在直线![]() 两侧,则
两侧,则![]() 的取值范围是 .
的取值范围是 .
12.![]() 的展开式中系数最小的项的系数为 .(用数字表示)
的展开式中系数最小的项的系数为 .(用数字表示)
13.已知平面上三点A、B、C满足![]() ,
,![]() ,
,![]() ,则
,则
![]() 的值等于 .
的值等于 .
14.光线每通过一块玻璃,其强度要失掉![]() 。把几块同样的玻璃重叠起来,通过它们的光线的强度减弱到原来强度的
。把几块同样的玻璃重叠起来,通过它们的光线的强度减弱到原来强度的![]() 以下,那么至少重叠 块玻璃(
以下,那么至少重叠 块玻璃(![]() )。
)。
15.过![]() 轴上一点
轴上一点![]() ,向圆
,向圆![]() 作切线,切点分别为
作切线,切点分别为![]() ,则四边形
,则四边形![]() 面积的最小值为
。
面积的最小值为
。
16.甲袋装有6个球,1个球标0,2个球标1,3个球标2;乙袋装有7个球,4个球标0,1个球标1,2个球标2。现从甲袋中取一个球,乙袋中取两个球。则取出的三个球上标有的数码之积为4的概率为 。
17.已知函数![]() ,给出下列四个命题:
,给出下列四个命题:
①![]() 为奇函数的充要条件是
为奇函数的充要条件是![]() ;
;
|
③当![]() 时,方程
时,方程![]() 的解集一定非空;
的解集一定非空;
④方程![]() 的解的个数一定不超过2个。
的解的个数一定不超过2个。
其中正确命题的序号是 。(写出所有正确命题的序号)
卷二
三、解答题
18.(本小题满分14分)已知![]() 为锐角,且
为锐角,且![]()
(I)求![]() 的值;
的值;
(II)求![]() 的值
的值
19.(本小题满分14分)已知![]() ,数列
,数列![]() 是首项为1,公差为2的等差数列。
是首项为1,公差为2的等差数列。
(I)求数列![]() 的通项公式;
的通项公式;
(II)求数列![]() 的前
的前![]() 项之和
项之和![]() 。
。
|
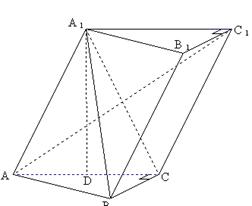 20.(本小题共14分)已知斜三棱柱
20.(本小题共14分)已知斜三棱柱![]() ,
,![]() ,
,![]() ,
,![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,又知
,又知![]() 。
。
(I)求证:![]() 平面
平面![]() ;
;
(II)求![]() 到平面
到平面![]() 的距离;
的距离;
(III)求二面角![]() 的大小。
的大小。
21.(本小题共14分)设![]() 分别为
分别为![]() 的重心和外心,
的重心和外心,![]() ,且
,且![]() 。
。
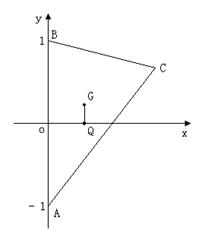 (I)求点
(I)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(II)若![]() 是过点
是过点![]() 且垂直于
且垂直于![]() 轴的直线,是否存在直线
轴的直线,是否存在直线![]() ,使得
,使得![]() 与曲线
与曲线![]() 交于两个不同的点
交于两个不同的点![]() ,且
,且![]() 恰被
恰被![]() 平分?若存在,求出
平分?若存在,求出![]() 的斜率的取值范围;若不存在,请说明理由。
的斜率的取值范围;若不存在,请说明理由。
|
22.已知函数![]() 处取得极值,且函数
处取得极值,且函数![]() 的图
的图
象经过点(1,0).
(I)求函数![]() 的解析式;
的解析式;
(II)设A、B为函数![]() 图象上任意相异的两个点,试判定直线AB和直线
图象上任意相异的两个点,试判定直线AB和直线![]() 的位置关系并说明理由;
的位置关系并说明理由;
(III)设函数![]() ,若对任意t、
,若对任意t、![]() 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
参考答案
卷一
一、选择题
1.选D 提示:在映射f作用下,四边形ABCD整体平移,面积不变
|
3.选B。提示:3的对面的数字是6,4 的对面的数字是2,故![]() 。
。
4.选C.提示:代入检验。
5.选C。提示:![]() 的最小正周期T=4,可得
的最小正周期T=4,可得![]()
6.选B。提示:设A∪B元素个数为y,可知10≤y≤16, y∈N,又由x = 18-y可得。
7.选B。提示:由已知,向量![]() 反向,
反向,![]() 。故
。故![]() 。
。
8.选A。提示:依题意:课外兴趣味小组由4名女生2名男生组成,共有![]() 种选法.其概率为
种选法.其概率为![]() 。
。
9.选C。提示:设![]() 代入
代入![]() 得
得![]() ,记
,记![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() 。
。
10.选C。提示:①正确;②正确,即为公垂线AB的中垂面;③存在,过AB中点![]() 作
作![]() 的平行线
的平行线![]() ,则
,则![]() 的平分线符合条件;④不正确,两条直线
的平分线符合条件;④不正确,两条直线![]() 可以相交。
可以相交。
二、填空题
11.![]() 。提示:由
。提示:由![]() 可知。
可知。
12.![]() 。提示:最小系数为
。提示:最小系数为![]() 。
。
13.![]() 。提示:
。提示:![]() ,
,![]()
![]()
14.11.提示:![]() ,
,![]() ,取
,取![]() 。
。
15.![]() 。提示:因
。提示:因![]() ,
,
故四边形![]() 面积的最小值为
面积的最小值为![]() 。
。
16.![]() 。提示:取出的三个球上标有的数码之积为4有两种情形:甲取标有数字1的球一个,乙取标有数字2的球两个;甲取标有数字2的球一个,乙取标有数字1和2的球各一个。取出的三个球上标有的数码之积为4的概率为
。提示:取出的三个球上标有的数码之积为4有两种情形:甲取标有数字1的球一个,乙取标有数字2的球两个;甲取标有数字2的球一个,乙取标有数字1和2的球各一个。取出的三个球上标有的数码之积为4的概率为![]() 。
。
17.①②③。提示:考查函数的基本性质,④可举反例:![]() 。
。
卷二
三、解答题
18.解:因为![]() 为锐角,且
为锐角,且![]() ,所以
,所以![]() 。————2分
。————2分
(I)则![]() 。————7分
。————7分
(II)![]()
![]()
![]()
![]() ————14分
————14分
19.解:(I)![]() ,
,![]() ;————4分
;————4分
(II)![]()
![]()
![]() ——8分
——8分
两式相减得![]() ————10分
————10分
![]() -
-
![]() ,————12分
,————12分
故![]() 。————14分
。————14分
20.解:(I)因为![]() 平面
平面![]() ,
,
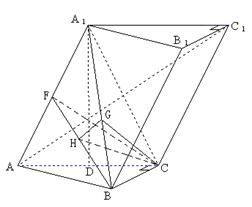 所以平面
所以平面![]() 平面
平面![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
得![]() ,又
,又![]()
所以![]() 平面
平面![]() ;————4分
;————4分
(II)因为![]() ,所以四边形
,所以四边形![]()
为菱形,
故![]() ,又
,又![]() 为
为![]() 中点,知
中点,知![]() 。
。
取![]() 中点
中点![]() ,则
,则![]() 平面
平面![]() ,从而面
,从而面![]() 面
面![]() ,
,
过![]() 作
作![]() 于
于![]() ,则
,则![]() 面
面![]() ,
,
在![]() 中,
中,![]() ,故
,故![]() ,
,
即![]() 到平面
到平面![]() 的距离为
的距离为![]() 。————9分
。————9分
(III)过![]() 作
作![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,
,
从而![]() 为二面角
为二面角![]() 的平面角,
的平面角,
在![]() 中,
中,![]() ,所以
,所以![]() ,
,
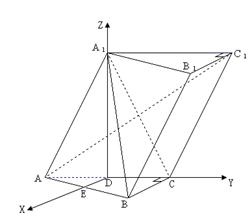 在
在![]() 中,
中,![]() ,
,
故二面角![]() 的大小为
的大小为![]() 。————14分
。————14分
解法2:(I)如图,取![]() 的中点
的中点![]() ,则
,则![]() ,因为
,因为![]() ,
,
所以![]() ,又
,又![]() 平面
平面![]() ,
,
以![]() 为
为![]() 轴建立空间坐标系,
轴建立空间坐标系,
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,由
,由![]() ,知
,知![]() ,
,
又![]() ,从而
,从而![]() 平面
平面![]() ;————4分
;————4分
(II)由![]()
![]() ,得
,得![]() 。
。
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,所以
,所以
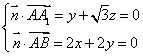 ,设
,设![]() ,则
,则![]()
所以点![]() 到平面
到平面![]() 的距离
的距离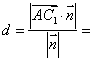
![]() 。——9分
。——9分
(III)再设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,所以
,所以
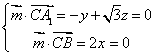 ,设
,设![]() ,则
,则![]() ,
,
故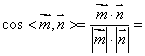
![]() ,根据法向量的方向,
,根据法向量的方向,
可知二面角![]() 的大小为
的大小为![]() 。————14分
。————14分
21.解:(I)设![]() ,则
,则![]() ,因为
,因为![]() ,可得
,可得![]() ;又由
;又由![]() ,
,
可得点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() 。————6分(没有
。————6分(没有![]() 扣1分)
扣1分)
(II)假设存在直线![]() ,代入
,代入![]() 并整理得
并整理得
![]() ,————8分
,————8分
设![]() ,则
,则![]()
![]() ————10分
————10分
又![]()
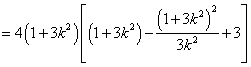
![]() ,解得
,解得![]() 或
或![]() ————13分
————13分
特别地,若![]() ,代入
,代入![]() 得,
得,![]() ,此方程无解,即
,此方程无解,即![]() 。
。
综上,![]() 的斜率的取值范围是
的斜率的取值范围是![]() 或
或![]() 。————14分
。————14分
22.解:(I)![]() ————3分
————3分
又![]() 故c=2,从而
故c=2,从而![]() 。————5分
。————5分
(II)直线AB和直线![]() 总相交。
总相交。
![]() ,由导数的几何意义可知,
,由导数的几何意义可知,
直线AB的
斜率![]() 而直线
而直线![]() 的斜率为
的斜率为![]() ,
,
所以两条直线相交。————9分
(III)![]() ,易知
,易知![]() 在
在![]() 递增,在
递增,在![]() 递减,
递减,
![]() 在x=0处有最大值2,————11分
在x=0处有最大值2,————11分
所以命题转化为![]() 对
对![]() 恒成立,即
恒成立,即![]() ,————12分
,————12分
设![]()
则有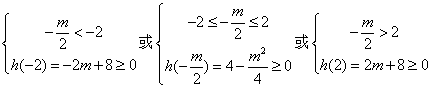
解得![]() 。————16分
。————16分