高三第二次月考数学（理科）
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．把选项填在答卷的表格中．
1．设集合A＝{x｜｜x－2｜≤2，x∈R}，B＝{y｜y＝－x2，－1≤x≤2}，则CR（A∩B）等于
A．R B．{x｜x∈R，x≠0} C．{0} D．
2．若复数
（a∈R，i为虚数单位）是纯虚数，则实数a的值为
A．－2 B．4 C．－6 D．6
3．设p：x2－x－20>0，q:
<0，则p是q的
A．充分不必要要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
4．为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17．5岁—18岁的男生体重（kg），得到频率分布直方图如下：
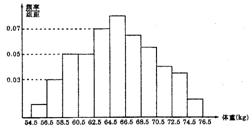
根据上图可得这100名学生中体重在［56．5，64．5］的学生人数是
A．20 B．30 C．40 D．50
5．设f （x）可导且下列各极限存在，则其中不成立的是
A．
B．
C．
D．
6．若函数f（x）＝
x3－f′（－1）x2＋x＋5，则f′（1）的值为
A．2 B．－2 C．－6 D．6
7．函数f （x）＝xsinx在x＝x0处取得极值，则（1＋x02）（1＋cos2x
）的值为
A．0 B．1 C．2 D．3
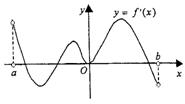8．函数f （x）的定义域为开区间（a,b），导函数f′（x）在（a,b）内的图象如图所示，则函数f（x）在开区间（a,b）内有极小值点
A．1个 B．2个
C．3个 D．4个
9．设x＝
，则
为
A．
B．2 C．
D．
10．已知函数y＝f （x）的图象与函数y＝ax（a>0且a≠1）的图象关于直线y＝x对称，记g（x）＝f （x）［f （x）＋f （2）－1］．若y＝g（x）在区间［，2］上是增函数，则实数a的取值范围是
A．
． B．（0,1）∪（1,2） C．
D．
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在答卷的相应位置．
11．某企业对一项工程的完成有三个方案，甲、乙、丙每个方案的获利情况如下表所示：
| 自然状况 | 方案甲 | 方案乙 | 方案丙 | |||
| 概率 | 获利（万元） | 概率 | 获利（万元） | 概率 | 获利（万元） | |
| 巨大成功 | 0．4 | 6 | 0．3 | 7 | 0．4 | 6．5 |
| 中等成功 | 0．3 | 2 | 0．4 | 2．5 | 0．2 | 4．5 |
| 不成功 | 0．3 | －4 | 0．3 | －5 | 0．4 | －4．5 |
问企业应选择哪种方案？____________________．
12．若
＝b，则b的值为_____________________．
13．已知定义在R上的函数f （x）满足下列条件：
（1）f （0）＝3；（2）f （x）>2，且
f （x）＝2；（3）当x∈R时，f ’（x）>0．
若f （x）的反函数是f 
－（x），则不等式f （x）<0的解集为_______________________．
14．已知点A（0，
），B（0，－），C（4＋，0）,其中n为正整数．设Sn表示ABC外接圆的面积，则
＝______________________．
三、解答题：本大题共6小题，每小题14分，共84分．解答应写出文字说明，证明过程或演算步骤．
15．甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0．6,被甲或乙解出的概率为0．92．
（1）求该题被乙独立解出的概率；
（2）求解出该题的人数
的分布列和数学期望．
16．已知函数f （x）＝x3＋ax2＋bx＋c在x＝－
与x＝1时都取得极值．
（1）求a、b的值及函数f （x）的单调区间;
（2）若对x∈［－1,2］,不等式f （x）<c
恒成立，求c的取值范围．
17．统计表明，某种型号的汽车在匀速行驶中每小时耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为：y＝
x3－
x＋（0<x≤120）．已知甲、乙两地相距100千米．
（1）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（2）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
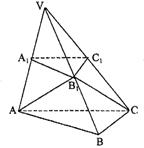18．如图，已知平面A1B1C1平行于三棱锥V—ABC的底面ABC，等边△AB1C所在的平面与底面ABC垂直，且∠ACB＝90°，设AC＝2a，BC＝a
（1）求证：直线B1C1是异面垂线AB1与A1C1的公垂线；
（2）求点A到平面VBC的距离；
（3）求二面角A—VB—C的大小．
19．已知函数f （x）＝－x2＋8x，g（x）＝6ln x＋m．
（1）求f （x）在区间［t，t＋1］上的最大值h（t）；
（2）是否存在实数m，使得y＝f（x）的图象与y＝g（x）的图象有且只有三个不同的交点？若存在，求出m的取值范围；若不存在，说明理由．
20．已知f（x）＝
，记数列{an}的前n项和为Sn，且有a1＝f （1），当n≥2时，Sn－
＝（n2＋5n－2）．
（1）计算a1，a2，a3，a4；
（2）求出数列{an}的通项公式并给予证明；
（3）求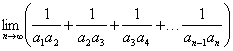
．
参考答案
一、选择题：本大题共10小题，每小题5分，共50分．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | A | C | D | D | C | A | C | D |
二、填空题：本大题共4小题，每小题4分，共16分．
11．甲 12．
13．（2,3） 14．4π
三、解答题：本大题共6小题，每小题14分，共84分．
15．（1）被乙独立解出的概率为0．8
（2）的分布列为
|
| 0 | 1 | 2 |
P | 0．08 | 0．44 | 0．48 |
E＝1．4
16．
（1）f （x）＝x3＋ax2＋bx＋c，f ′（x）＝3x2＋2ax＋b
由f′（）＝
a＋b＝0，f ′（1）＝3＋2a＋b＝0得a＝－，b＝－2
f ′＝3x2―x―2＝（3x＋2）（x－1），函数f（x）的单调区间如下表：
| x | （－ |
| （ | 1 | （1， |
| f′（x） | ＋ | 0 | － | 0 | ＋ |
| f （x） | ↑ | 极大值 | ↓ | 极小值 | ↑ |
）
）所以函数f（x）的递增区间是（－∞，
）与（1，＋∞），递减区间是（，1）
（2）f（x）＝x3－x2－2x＋c，x∈（－1，2），
当x＝时，f（x）＝
＋c为极大值，
而f（2）＝2＋c,则f （2）＝2＋c为最大值．
要使f （x）<c2（x∈（－1，2））恒成立，只需c2>f（2）＝2＋c
解得c<－1或c>2
17．
（1）当x＝40时，汽车从甲地到乙地行驶了
＝2.5小时，要耗油（×403－×40＋8）×2.5＝17.5（升）．
当汽车以40千米/小时，汽车从甲地到乙地行驶了
小时，设耗油量为h（x）升，依题意得h（x）＝（x3－x＋8）·＝
x2＋
－
（0<x<120），
h′（x）＝
（0<x≤120）
令h′（x）＝0，得x＝80
令x∈（0,80）时，h′（x）<0，h（x）是减函数
当x∈（80,120）时，h′（x）>0，h（x）是增函数
∴当x＝80时，h（x）取到极小值h（80）＝11.25
因为h（x）在（0,120）上只有一个极值，所以它是最小值．
答：当汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为11.25升．
18．（1）证明:略
（2）A到平面VBC的距离为
．
（3）二面角A—VB—C的大小为arccos
．
19．
（1）f （x）＝－x2＋8x＝－（x－4）2＋16,
当t＋1<4，即t<3时，f（x）在［t，t＋1］上单调递增，h（t）＝f （t＋1）
＝－（t＋1）＋8（t＋1）＝－t2＋6t＋7;
当t≤4≤t＋1时，即3≤t≤4时，h（t）＝f（4）＝16;
当t>4时，f （x）在[t，t＋1]上单调递减，h（t）＝f （x）＝－t2＋8t
综上，h（t）＝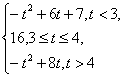
（2）函数y＝f （x）的图象与y＝g（x）的图象有且只有三个不同的交点，即函数
（x）＝g（x）－f （x）的图象与x轴的正半轴有且只有三个不同的交点．
∴（x）＝x2－8x＋16ln x＋m，
∵2（x）＝2x－8＋
＝
当x∈（0,1）时，2（x）>0, （x）是增函数;
当x∈（1,3）时，2（x）<0，（x）是减函数;
当x∈（3，＋∞）时，2（x）>0, （x）是增函数;
当x＝1，或x＝3时，2（x）＝0;
∴（x）
=（1）＝m－7，（x）
＝（3）＝m＋6ln 3－15．
∵当x充分接近0时，（x）<0，当x充分大时，（x）>0．
∴要使（x）的图象与x轴正半轴有三个不同的交点，必须且只须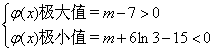
，即7<m<－6ln 3.
所以存在实数m，使得函数y＝f （x）与y＝g（x）的图象有且只有三个不同的交点，m的取值范围为（7，15－6ln 3）．
20．（1）a1＝2，a2＝3，a3＝4，a4＝5；
（2）an＝n＋1;可用数学归纳法证明
（3）