高三第二次月考数学（文科）
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．把选项填在答卷的表格中．
1．若集合M＝{x｜x－2<0}，N＝{x｜｜x－1｜<2}，则M∩N＝
A．{x－2<x<2} B．{xx<2} C．{x－1<x<2} D．{x－1<x<3}
2．函数y＝x3－3x在［－1,2］上的最小值是
A．0 B．－4 C．2 D．－2
3．设集合M＝{xx>2}，P＝{xx<3}，那么“x∈M或x∈P”是“x∈M∩P”的
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．非充分非必要条件
4．已知f（x）＝1－（x－a）（x－b），并且m，n是方程f（x）＝0的两根，则实数a,b,m,n的大小关系可能是
A．m<a<b<n B．a<m<n<b C．a<m<b<n D．m<a<n<b
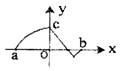5．已知函数f（x）的定义域为［a,b］，函数f（x）的图象如右图所示，则函数f（x）的图象是
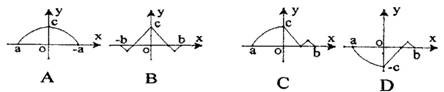
6．对于R上可导的任意函数f（x），若满足（x－1）·f’′（x）≥0，则必有
A．f（0）＋f（2）<2f（1） B．f（0）＋f（2）≤2f（1）
C．f（0）＋f（2）≥2f（1） D．f（0）＋f（2）＞2f（1）
7．已知f（x）是R上的增函数，点A（－1,1），B（1,3）在它的图象上，f－1（x）是它的反函数，那么不等式f－1（log2 x）<1的解集为
A．{x－1<x<1} B．{x2<x<8} C．{x1<x<3} D．{x0<x<3}
8．已知函数f（x）＝x3＋ax2＋bx＋a2在x＝1处有极值10，则f（2）等于
A．11或18 B．18 C．11 D．17或18
9．一水池有2个进水口，一个出水口，进出水速度如图甲、乙所示．某天0点到6点，该水池的蓄水量如图丙所示．（至少打开一个水口）
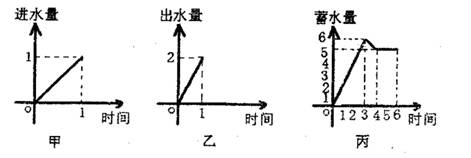
给出以下3个论断：
①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水，则一定能确定正确的诊断是
A．① B．①② C．①③ D．①②③
10．函数f（x）对作实数x满足f（x＋2）＝－
，若f（1）＝－5,则f（f（5）＝
A．
B．－ C．5 D．－5
二、填空题：（本大题殿4小题，每小题4分，共16分．）
11．满足{1}
M
{1,2,3,4}的集合M有_______个．
12．函数y＝（0．2）x2－6x＋8的单调递增区间是________．
13．P为函数y＝x3－x＋2图象上的任意一点，其关于点Q对称的点P1也必在其图象上，则点Q的坐标为________．
14．定义运算a*b为a*b＝
，例如，1*2＝1,则函数f（x）＝x*（x2－x）的值域为________．
三、解答题：（本大题共6小题，每题14分，共84分．解答题写出必要的文字说明、证明过程以及演算步骤．）
15．已知集合A＝{xax2－2x＋1＝0，x∈R}．
（1）若A＝
，求实数a的取值范围；
（2）若A是单元素集，求实数a的值以及集合A．
16．已知函数f（x）＝
（x∈R），且它的反函数记为f－1（x）．
（1）求f－1（x）的解析式；
（2）求y＝f－1 （x）在点（－2, f－1（x））处的切线方程．
17．已知函数f（x）在R上有定义，且满足f（x）＋xf（1－x）＝x．
（1）求f（x）的解析式；
（2）求y＝f（x）的值域．
18．已知函数f（x）＝loga
（a>0，a≠1,）．
（1）求函数f（x）的定义域；
（2）解不等式f（x）≥loga（3x）．
19．已知实数m>0，函数f（x）＝2x3＋（m－x）3，
（1）判断函数f（x）的奇偶性，并说明理由；
（2）f（x）在［5,＋∞］上单调递增，求m的范围．
20．设n为正整数，规定：fn（x）＝
，已知f（x）＝
．
（1）设集合A＝{0，1，2}，对任意x∈A，证明：f3（x）＝x；
（2）探求f2003（
）
参考答案
一、选择题：本大题共10小题，每小题5分，共50分．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | B | A | B | C | B | B | A | A |
二、填空题：本大题共4小题，每小题4分，共16分．
11．7 12．［－∞，3］ 13．（0，2） 14．R
三、解答题：（本大题共6小题，每题14分，共84分．解答题写出必要的文字说明、证明过程以及演算步骤．）
15．（1）a∈（1，＋∞）
（2）a＝0，A＝
，a＝1，A＝{1}
16．（1）f－1（x）＝x3＋2（x∈R）
（2）y＝12x＋18
17．（1）f（x）＝
（2）y∈［0，
］
18．（1）x∈（－2,2）
（2）当a>1时，不等式的解集为
当1>a>0时，不等式的解集为
19．（1）非奇非偶函数；
（2）m∈
20．（1）f3（0）＝f2（2）＝f1（1）＝0; f3（1）＝f2（0）＝f1（2）＝1; f3（2）＝f2（1）＝f1（0）＝2;∴结论成立．
（2）
∴f2003