高三第一学期模拟考试数学试题(文)
考试时间120分钟 满分150分
一、选择题(满分60分,每小题只有一个正确答案,请将正确答案的字母涂在机读卡上)
1.函数![]() 的定义域为 ( )
的定义域为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知α为第二象限的角,则![]() 所在的象限是 ( )
所在的象限是 ( )
A.Ⅰ,Ⅱ B.Ⅰ,Ⅲ C.Ⅱ,Ⅳ D.Ⅱ,Ⅲ
3.已知![]() ,则
,则![]() 的最大项是 ( )
的最大项是 ( )
A.a1 B.a2 C.a3 D.a4
4.若,p,![]() 成立的一个充分不必要条件是 ( )
成立的一个充分不必要条件是 ( )
A.q > p >0 B.p > q >0 C.p < q <0 D.p = q ≠0
5.把函数![]() 的图象按向量
的图象按向量![]() 平移,得到函数
平移,得到函数![]() 的图象,则向量
的图象,则向量![]() ( )
( )
A.(-3,-4) B.(3,4) C.(-3,4) D.(3,-4)
6.在△ABC中,a =
5,b = 8,C = 60°,则![]() = ( )
= ( )
A.20 B.-20 C.![]() D.
D.![]()
7.各项均不为零的等差数列![]() 中,若
中,若![]() 则S2006-2006 =( )
则S2006-2006 =( )
A.0 B.-2006 C.2006 D.4012
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.集合P={1,4,9,16…},若![]() 则
则![]() ,则运算
,则运算![]() 可能是 ( )
可能是 ( )
A.加法 B.减法 C.除法 D.乘法
10.在△ABC中,![]() ,若△ABC的最长边为
,若△ABC的最长边为![]() ,则最短边的长为( )
,则最短边的长为( )
|
11.![]() 为等差数列,若
为等差数列,若![]() ,且它的前n项和Sn有最小值,那么当Sn取得最小正值时,n = ( )
,且它的前n项和Sn有最小值,那么当Sn取得最小正值时,n = ( )
A.11 B.17 C.19 D.21
12.设对任意实数![]() ,不等式
,不等式![]() 总成立,则实数a的取值范围是( )
总成立,则实数a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(满分16分,每小题4分)
13.![]() 为等比数列,a1=1,a5 = 9,a3 = .
为等比数列,a1=1,a5 = 9,a3 = .
14.已知![]() .
.
15.函数![]() 的反函数为
.
的反函数为
.
16.设函数![]() ,给出下列命题①f (x)有最小值;②当a = 0时,f (x)的值域为R;③当a > 0时,f (x)在
,给出下列命题①f (x)有最小值;②当a = 0时,f (x)的值域为R;③当a > 0时,f (x)在![]() 上有反函数;④若f (x)在
上有反函数;④若f (x)在![]() 上单增,则
上单增,则
a≥-4.其中正确命题的序号为 .
三、解答题(满分 74分)
17.(12分)一个口袋内装有大小相同且已编有不同号码的6个黑球和4个红球,某人一次从中摸出2个球
(Ⅰ)如果摸到的球中含有红球就中奖,那么此人中奖的概率是多少?
(Ⅱ)如果摸到的2个球都是红球,那么就中大奖,在有放回的3次摸球中,此人恰好两次中大奖的概率是多少?
18.(12分)函数![]() ,
,
(Ⅰ)求![]() 的最小正周期
的最小正周期
(Ⅱ)若![]() 时,求
时,求![]() 的最小值
的最小值
(Ⅲ)设有不相等的实数![]() 的值
的值
|
19.(12分)已知两个不共线的向量![]() 的夹角为
的夹角为![]()
(1)若![]() 垂直,求
垂直,求![]() 的值
的值
(2)若![]() 的最小值及对应的x的值,并指出向量
的最小值及对应的x的值,并指出向量![]() 的位置关系
的位置关系
20.(12分)已知数列![]() 为等差数列,且
为等差数列,且![]()
(Ⅰ)求![]()
(Ⅱ)求证![]()
21.(12分)某公司生产的A型商品通过租赁柜台进入某商场销售,第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件,第二年商场开始对该商品征收比率为p%的管理费,(即销售100元要征收p元),于是该商品的定价上升为每件![]() 元,预计的销售量将减少p万件
元,预计的销售量将减少p万件
(Ⅰ)将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域.
(Ⅱ)要使第二年商场在此项经营收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
22.(12分)已知定义在R上的函数![]() 满足
满足![]() ,当x < 0时,f (x) < 0
,当x < 0时,f (x) < 0
(Ⅰ)求证f (x)为R上的增函数
(Ⅱ)当a
> 2时,解关于x的不等式![]()
参考答案
一、选择题
1.B 2.B 3.C 4.A 5.A 6.B 7.C 8.A 9.D 10.D
11.C 12.C
二、填空题
13.![]() 14.
14.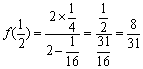 15.
15.![]() 16.②③
16.②③
三、解答题
17.解:(Ⅰ)记“从袋中摸出的2个球中含有红球”为事件A
则![]() …………………………………………4分
…………………………………………4分
(Ⅱ)记“从袋中摸出的2个球都是红球”为事件B
则![]() ………………………………………………8分
………………………………………………8分
3次摸球恰好有两次中大奖相当于作了3次独立重复实验
则![]() …………………12分
…………………12分
18.解:![]()
……………………3分
(Ⅰ)![]()
(Ⅱ)当![]()
∴当![]() ……………………………………………………9分
……………………………………………………9分
(Ⅲ)![]()
由![]()
![]()
![]()
![]()
![]() ……………………12分
……………………12分
19.解:(1)由题意得:![]()
![]()
![]() ……………………………………………………………………5分
……………………………………………………………………5分
(2)![]()
![]()
∴当![]() 有最小值为
有最小值为![]() …………………………………10分
…………………………………10分
此时![]()
![]() 垂直 …………………………………………………………12分
垂直 …………………………………………………………12分
20.解:(Ⅰ)设等差数列![]() 的公差为d
的公差为d
第一项为 ![]()
第三项为 ![]()
∴公差d = 1 ………………………………………………………………3分
![]()
![]()
![]() …………………………………………………………6分
…………………………………………………………6分
(Ⅱ)![]()
![]()
![]() …………………………12分
…………………………12分
21.解:(Ⅰ)由题意:第二年该商品年销售量为(11.8-p)万件,年销售收入为![]() 万元,则商场该年对该商品征收的总管理费为
万元,则商场该年对该商品征收的总管理费为![]() p%万元,故所求函数为:
p%万元,故所求函数为:![]() ………4分
………4分
(Ⅱ)由![]() ,即
,即![]()
![]()
故当比率在[2%,10%]内时商场收取的管理费将不少于14万元 ……………8分
22.(Ⅰ)证明:任取![]() ,则
,则![]() ,
,
由已知得![]() ……………………………………………………3分
……………………………………………………3分
又![]()
![]()
![]()
![]() 为R上的增函数 …………………………………………………… 6分
为R上的增函数 …………………………………………………… 6分
(Ⅱ)解:原不等式化为![]()
即![]()
![]()
![]() 为R上的增函数
为R上的增函数
![]() ………………………………………………9分
………………………………………………9分
即![]()
![]()
![]() ……………………………………………… 12分
……………………………………………… 12分