
 高三第一学期期中考试数学试题
高三第一学期期中考试数学试题![]()
考试时间:120分钟 试卷分值:150分
命题人:魏国勇
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共60分,每小题5分,答案必须用2B铅笔在答题卡中相应的位置,否则该题不予记分。)
1、设集合![]() 若
若![]() ,则
,则![]() 与
与![]() 的关系
的关系
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、设![]() ,则
,则![]() 是
是![]() ( )条件
( )条件
A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要
3、已知函数![]() 是区间
是区间![]() 上的减函数,则实数
上的减函数,则实数![]() 的取值范围是
的取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、函数![]() 定义域为R且x≠1,已知
定义域为R且x≠1,已知![]() 为奇函数,当
为奇函数,当![]() 时
时![]() ,那么
,那么![]() 时
时![]() 递减区间是
递减区间是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、函数![]() 是定义域为R的偶函数,又是以2为周期的周期函数,若
是定义域为R的偶函数,又是以2为周期的周期函数,若![]() 在
在![]() 上是减函数,那么
上是减函数,那么![]() 在
在![]() 上是
上是
A、增函数 B、减函数 C、先增后减的函数 D、先减后增的函数
6、(理)若复数z满足![]() ,则复数
,则复数![]() 的值
的值
A、1 B、-1 C、![]() D、
D、![]()
(文)曲线![]() 的对称中心不是
的对称中心不是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、等差数列![]() 中,
中,![]() ,则
,则![]() 等于
等于
A、-1221 B、-21.5 C、-20.5 D、-20
8、已知![]() 的周期为
的周期为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、设![]() ,
,![]() ,
,![]() 点P是线段AB上的一个动点,
点P是线段AB上的一个动点,![]() 若
若![]() ,则实数λ取值范围是
,则实数λ取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、从0到9这10个数字中任取3个数字组成一个没有重复数字的三位数,这个数不能被3整除的概率为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、已知,a、b、c是实常数且![]() ,
,![]() ,则
,则![]() 的值是
的值是
A、![]() B、
B、![]() C、
C、![]() D、6
D、6
12、若曲线![]() 上任一点处切线的倾角都是锐角,那么整数a的值等于
上任一点处切线的倾角都是锐角,那么整数a的值等于
A、-2 B、0 C、1 D、-1
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共16分,每小题4分)
13、已知![]() 并且
并且![]() 的最小值为
的最小值为![]() ,则实数
,则实数![]() 的取值范围是
。
的取值范围是
。
14、在数列![]() 中,
中,![]()
![]() ,则使
,则使![]() 成立的n值是
。
成立的n值是
。
15、已知![]() 且
且![]() ,则
,则![]() 。
。
16、已知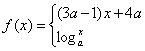
![]() 是
是![]() 的减函数,那么
的减函数,那么![]() 。
。
三、解答题
17、解关于x的不等式:![]() (其中
(其中![]() 且
且![]() )。
)。
18、求函数![]() 在
在![]() 上的最大值。
上的最大值。
19、某篮球选手每次投篮命中概率为0.4,各次投篮间相互独立,令此选手投篮n次的命中率为![]() (
(![]() 为进球数与n之比)试分别求以下发生的概率(用分数作答)。
为进球数与n之比)试分别求以下发生的概率(用分数作答)。
(1)![]()
(2)![]() ,
,![]()
20、某俱乐部准备承办一场足球赛,预计共卖出门票2.4万张,票价有3元、5元、8元三种,且票价3元和5元的张数的积为0.6万张,设x是门票的总收入,经预算扣除其他各项支出后,该俱乐部的纯收入函数为![]() 试问三种门票分别卖多少张时,纯收入最多。
试问三种门票分别卖多少张时,纯收入最多。
21、(理)已知![]() (1)求
(1)求![]() 的反函数及
的反函数及![]() 的导函数。(2)假设
的导函数。(2)假设![]() ,不等式:
,不等式:![]() 恒成立求m范围。
恒成立求m范围。
(文)已知![]() ,函数
,函数![]() ,设
,设![]() ,记曲线
,记曲线![]() 在点
在点![]() 处切线
处切线![]() 。(1)求
。(1)求![]() 方程。(2)
方程。(2)![]() 与x轴交于
与x轴交于![]() ,若
,若![]() ,证明:
,证明:![]()
22、已知![]() 在(-1,1)上有意义,
在(-1,1)上有意义,![]() 且满足
且满足![]() 、
、![]() 时,有
时,有![]() 。
。
(1)证明:![]() 在(-1,1)上为奇函数。
在(-1,1)上为奇函数。
(2)数列![]() 满足
满足![]() ,
,![]() 设
设![]() ,求
,求![]() 的道项公式。
的道项公式。
(3)求![]() 的值。
的值。