高三第一学期期中数学统练试题(理科)
班级_________ 姓名_________ 学号__________ 分数__________
总分150分
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,恰有一项是符合题目要求的。
1.已知集合P={x∈N1≤x≤10},集合Q={x∈Rx2+x-6≤0},则P∩Q等于( )
A.{2} B.{1,2} C.{2,3} D.{1,2,3}
2.函数![]() 的反函数是( )
的反函数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.函数![]() 的导数是( )
的导数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.在下列函数中,值域是(0,+∞)的函数是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若函数f (x)=logx2在(0,∞)上是减函数,则a的取值范围是( )
A.a>1 B.a< C.a> D.1<a<
6.若![]() ,则
,则![]() 等于
( )
等于
( )
A.![]() B.
B.![]() C.3 D.2
C.3 D.2
7.随机变量ξ的概率分布规律为![]() 其中a是常数,则
其中a是常数,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]() 设
设![]()
![]() 则( )
则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共6小题,每小题5分,共30分。不需要写出解答过程,请把答案直接填在相应位置上。
9.设函数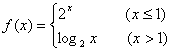 ,则不等式
,则不等式![]() 的解集为_________________。
的解集为_________________。
10.若函数y=lg(4-a·2x)的定义域为{xx£1},则实数a的取值范围是__________。
11.已知函数![]() 若
若![]() 为奇函数,则
为奇函数,则![]() ________。
________。
12.曲线![]() 在点
在点![]() 处的切线方程为_______________。
处的切线方程为_______________。
13.假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第8行第7列的数开始向右读,请你衣次写出最先检测的5袋牛奶的编号__________________________________(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
14.让4个相同的白球和3个相同的黑球,随机地排成一行,不同的排法有m种,其中有且仅有2个黑球相邻的排法为n种,则=___________________。(用数字作答)
三、解答题:本大题共6小题,共80分。解答时应写出文字说明、证明过程或演算步骤。
15.(本题13分)已知函数![]() (k为常数),
(k为常数),![]() 是函数
是函数![]() 图象上的点
图象上的点
(1)求实数k的值及反函数![]() 的解析式;
的解析式;
(2)将![]() 的图象沿x轴向右平移3个单位,得到函数
的图象沿x轴向右平移3个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 的最小值。
的最小值。
16.(本题13分)已知函数![]() 的图象都过点P(2,0),且在点P处有相同的切线.
的图象都过点P(2,0),且在点P处有相同的切线.
(1)求实数a,b,c的值;
(2)设函数F(x)=f(x)+g(x),求函数![]() 的极值.
的极值.
17.(本题13分)甲、乙、丙3人投篮,投进的概率分别是, , .
(Ⅰ)现3人各投篮1次,求3人都没有投进的概率;
(Ⅱ)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ.
18.(本题13分)已知m³0,研究函数![]() 的单调区间.
的单调区间.
19.(本题14分)已知函数![]() 的定义域为R(实数集),
的定义域为R(实数集),
且对于任意实数x,y总有![]() 成立.
成立.
(Ⅰ)试说明函数y=f(x)的图象必通过(0,0)点,或通过(0,1)点;
(Ⅱ)若存在![]() 使得
使得![]() ,试证对于任意
,试证对于任意![]() ,
,![]() 总成立;
总成立;
20.(本题14分)已知二次函数![]() R)满足
R)满足![]() ,对任意实数x,都有
,对任意实数x,都有![]() ,且
,且![]() 时,总有
时,总有![]() .
.
(1)求![]() ;
;
(2)求a,b,c的值;
(3)当![]() ,
,![]() 时,函数
时,函数![]() (m
(m![]() R)是单调函数,求m的取值范围.
R)是单调函数,求m的取值范围.
高三理科参考答案
一、选择题
1.B 2.A 3.B 4.D 5.D 6.B 7.D 8.D
二、填空题
9.![]() 或
或![]()
10.a£2
11.![]()
12.![]()
13.785,567,199,507,175
14.4/7
三、解答题
15.解:(1)![]()
(2)![]()
![]() (当
(当![]() 时取等号)
时取等号)
![]()
16.解:(Ⅰ)因为函数![]() 的图象都过点P(2,0),
的图象都过点P(2,0),
所以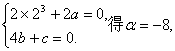
![]()
![]()
又当![]()
所以,![]()
(Ⅱ)因为![]()
由![]()
由![]()
所以,当![]()
当![]()
当x=-2时,函数F(x)取得极大值为0
当x=2/3时,函数F(x)取得极小值为-512/27
17.解: (Ⅰ)记"甲投篮1次投进"为事件A1 , "乙投篮1次投进"为事件A2 , "丙投篮1次投进"为事件A3, "3人都没有投进"为事件A . 则 P(A1)= , P(A2)= , P(A3)= ,
∴ P(A) = P()=P()·P()·P()
= [1-P(A1)] ·[1-P (A2)] ·[1-P (A3)]=(1-)(1-)(1-)=
∴3人都没有投进的概率为 .
(Ⅱ)解法一: 随机变量ξ的可能值有0,1,2,3), ξ~ B(3, ),
P(ξ=k)=C3k()k()3-k (k=0,1,2,3) , Eξ=np = 3× = .
解法二: ξ的概率分布为:
| ξ | 0 | 1 | 2 | 3 |
| P |
Eξ=0×+1×+2×+3×= .
18.解:![]()
=![]() .…………
.…………
记![]() 只需讨论
只需讨论![]() 的正负即可.
的正负即可.
(1)当![]()
当![]()
![]()
(2)当![]() ,
,
(a)当![]() 在区间
在区间![]()
![]() 在此区间上是减函数;在区间
在此区间上是减函数;在区间![]()
![]() 在此区间上是增函数;
在此区间上是增函数;
(b)当![]()
![]() 处连续,
处连续, ![]() 在
在![]() 上是减函数;
上是减函数;
©当![]() ,在区间
,在区间![]()
![]() 在此区间上是减函数;
在此区间上是减函数;
在区间![]()
![]() 在此区间上是增函数.
在此区间上是增函数.
19.(Ⅰ)解
在![]() 中 令x=y=0
中 令x=y=0
则 ![]()
得 ![]() 或
或![]()
即函数![]() 的图象通过(0,0)点或通过(0,1)点.
的图象通过(0,0)点或通过(0,1)点.
(Ⅱ)证明 对于任意实数x,可知
![]()
![]() (*)
(*)
另外,![]()
![]()
可知 ![]() (**)
(**)
由(*)、(**)可以推得:对于任意![]() ,总有
,总有![]() 成立.
成立.
20.解
(1)![]() 对任意实数x,都有
对任意实数x,都有![]() ,所以
,所以![]() ,又
,又![]() 在
在![]() 时,有
时,有![]() ,故
,故![]() ,因此有
,因此有![]() .
.
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,因为
,因为![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取等号).又因为对任意实数x,都有
时取等号).又因为对任意实数x,都有![]() ,所以
,所以![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立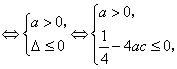 故
故![]() 且
且![]() ,因此有
,因此有![]() ,从而
,从而![]()
![]()
(3)![]()
![]()
![]() ,
,![]() 的对称轴是
的对称轴是![]() ,因为
,因为![]() (m
(m![]() R)在
R)在![]() ,
,![]() 上是单调函数,所以
上是单调函数,所以![]() 或
或![]()