| 函数综合试题 |
| 山东省苍山县第一中学 |
| 姓名 考号 |
一:选择题
1.已知![]() ,则
,则![]() 则A等于
( )
则A等于
( )
A.15
B.![]() C.
C.![]() D.225
D.225
2.若0<a<1,且函数![]() ,则下列各式中成立的是( )
,则下列各式中成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知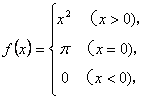 则
则![]() 的值等于( )
的值等于( )
A.0
B.![]() C.
C.![]() D.9
D.9
4.若![]() ,则( )
,则( )
A.a<b<c B.c<b<a C.c<a<b D.b<a<c
5.已知实数a、b满足等式![]() ,下列五个关系式: ① 0<a<b<1;② 0<b<a<1; ③ a=b;④ 1<a<b;⑤ l<b<a.其中不可能成立的关系式有( )
,下列五个关系式: ① 0<a<b<1;② 0<b<a<1; ③ a=b;④ 1<a<b;⑤ l<b<a.其中不可能成立的关系式有( )
A.1个 B.2个 C.3个 D.4个
6.若0<a<1,且函数![]() ,则下列各式中成立的是( )
,则下列各式中成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知:![]() 的不等实根一共有( )
的不等实根一共有( )
A、1个 B、2 个 C、3 个 D、4个
8.在计算机的算法语言中有一种函数![]() 叫做取整函数(也称高斯函数),它表示
叫做取整函数(也称高斯函数),它表示![]() 的整数部分,即[
的整数部分,即[![]() ]是不超过
]是不超过![]() 的最大整数.例如:
的最大整数.例如:![]() .设函数
.设函数![]() ,则函数
,则函数![]() 的值域为
( )
的值域为
( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.
![]()
9.曲线![]() 在原点处的切线方程为
在原点处的切线方程为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设函数![]() 有( )
有( )
A.分别位于区间(1,2),(2,3),(3,4)内的三个根
B.四个实根![]()
C.分别位于区间(0,1),(1,2),(2,3),(3,4)内的四个根
D.分别位于区间(0,1)(1,2),(2,3),内的三个根
11.函数![]() 的导数是( )
的导数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
12.与定积分![]() 相等的是( )
相等的是( )
A.![]() B.
B.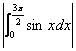 C.
C. ![]() -
-![]() D.
D.
![]() +
+![]()
二:填空题
13.由曲线![]() 所围成的图形面积是
.
所围成的图形面积是
.
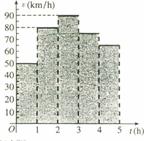
14.一辆汽车在某段路程中的行驶速度![]() 与时间
与时间![]() 的关系如图所示,则该汽车在前3小时内行驶的路程为_________km,假设这辆汽车的里程表在汽车行驶这段路程前的读数为2006km,那么在
的关系如图所示,则该汽车在前3小时内行驶的路程为_________km,假设这辆汽车的里程表在汽车行驶这段路程前的读数为2006km,那么在![]() 时,汽车里程表读数
时,汽车里程表读数![]() 与时间
与时间![]() 的函数解析式为__________。
的函数解析式为__________。
15. 函数f(x)=x3-3x2+6x-7的图象是中心对称图形, 其对称中心的坐标为_________ 。
16.给出下列四个命题:
①函数![]() (
(![]() 且
且![]() )与函数
)与函数![]() (
(![]() 且
且![]() )的定义域相同;
)的定义域相同;
②函数![]() 与
与![]() 的值域相同;
的值域相同;
③函数![]() 与
与![]() 都是奇函数;
都是奇函数;
④函数![]() 与
与![]() 在区间[0,+
在区间[0,+![]() )上都是增函数。
)上都是增函数。
其中正确命题的序号是_____________。(把你认为正确的命题序号都填上)
三:解答题
17.(12分)设f (x)=lg(ax2-2x+a),
(1) 如果f (x)的定义域是(-∞, +∞),求a的取值范围;
(2) 如果f (x)的值域是(-∞, +∞),求a的取值范围。
18.(12分)统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=![]() (0<x≤120).已知甲、乙两地相距100千米。
(0<x≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
19.(12分)设![]() , 点P
, 点P![]() 是函数
是函数![]() 的图象的一个公共点, 两函数的图象在点P处有相同的切线.
的图象的一个公共点, 两函数的图象在点P处有相同的切线.
(1) 用![]() 表示a, b, c;
表示a, b, c;
(2) 若函数![]() 在
在![]() 上单调递减,求
上单调递减,求![]() 的取值范围.
的取值范围.
20.(12分)设函数![]() , 其中
, 其中![]() ,
,![]() 是
是![]() 的导函数.
的导函数.
(1)若![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)若![]() ,函数
,函数![]() 的两个极值点为
的两个极值点为![]() 满足
满足![]() . 设
. 设![]() , 试求实数
, 试求实数![]() 的取值范围.
的取值范围.
21.(14分)已知函数![]() ,
,![]() ,且
,且![]() 有极值.
有极值.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求函数![]() 的值域;
的值域;
(3)函数![]() ,证明:
,证明:![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
22.(12分)设f(x)是定义在[0,1]上的函数,若存在x*∈(0,1),使得f(x)在[0, x*]上单调递增,在[x*,1]上单调递减,则称f(x)为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.对任意的[0,l]上的单峰函数f(x),下面研究缩短其含峰区间长度的方法.
(1)证明:对任意的x1,x2∈(0,1),x1<x2,若f(x1)≥f(x2),则(0,x2)为含峰区间;若f(x1)≤f(x2),则(x*,1)为含峰区间;
(2)对给定的r(0<r<0.5=,证明:存在x1,x2∈(0,1),满足x2-x1≥2r,使得由(I)所确定的含峰区间的长度不大于0.5+r;
(3)选取x1,x2∈(0,1),x1<x2,由(I)可确定含峰区间为(0,x2)或(x1,1),在所得的含峰区间内选取x3,由x3与x1或x3与x2类似地可确定一个新的含峰区间.在第一次确定的含峰区间为(0,x2)的情况下,试确定x1,x2,x3的值,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0.34.(区间长度等于区间的右端点与左端点之差)