三次函数性质的探索
摘要 本文利用数学软件Mathcad，以导数为工具，对三次函数的单调性、极值、切线、对称性等问题进行探索研究，经过实验验证，深刻挖掘三次函数的性质，为高考有关问题找到了有效的解决方法．
关键词 三次函数的性质 极值 导数 Mathcad
一、二次函数是重要的且具有广泛应用的基本初等函数已是不争的事实，在初等数学范畴内利用直观的初等方法，学生对此已有较为全面、系统、深刻的认识，并在某些方面具备了把握规律的能力。然而，三次多项式函数虽然同样初等，但是诸多问题的研究与探讨学生均显力不从心。目前，研究函数性质的高等工具—导数，已进入中学课堂，使三次函数成为高考数学的一大亮点，特别是文科数学,作为教者理应力所能及地借助于这一工具让学生对三次多项式函数能有一些初步的理性认识。
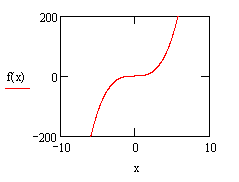
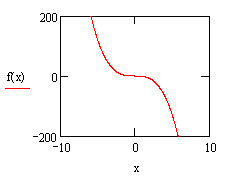
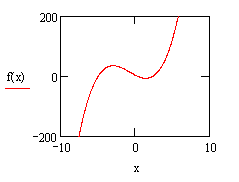
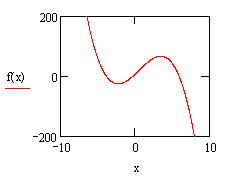
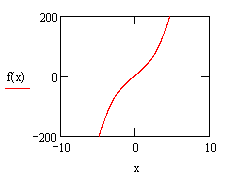
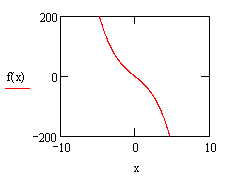
三次函数
有什么性质？各系数对它的图象和性质有何影响？首先还得对它有感性的认识，通过Mathcad输入不同的参数进行探索，经过多次的实验、猜测、归纳发现它的图象有六种，如图：
|
|
|
|
|
|
进行求导：
是二次函数，原函数的极值点与单调性与导函数的正负有关，所以容易发现导函数中的参数
与
的符号起决定性作用。当为正时，原函数的图象应为上图中的（1）、（3）、（5）三种情况；而当为负时，原函数的图象则为（2）、（4）、（6）三种情况。当
时，二次方程
有两相异实根
，且在的两边
的符号相反，故函数
存在两个极值点，图象为上图中的（3）、（4）两种；当
时，二次方程有两相等实根，且在根的两边
的符号相同，这时函数只存在驻点（但不是极值点），函数的图象为上图中（1）、（2）两种，当
时；方程无实根，的值恒为正（或负），函数的图象为上图中的（5）、（6）两种。
仔细观察图象,我们还不难发现三次函数是中心对称曲线，这一点可以得到进一步的验证:设
，得
整理得，
。据多项式恒等对应系数相等,可得
且
，从而三次函数是中心对称曲线，且由
知其对称中心
仍然在曲线上。而是否具有特殊的意义？对函数进行两次求导，
再令等于0，得
,恰好是对称中心的横坐标，这可不是巧合，因为满足
的
正是函数拐点的横坐标，这一性质刚好与图象吻合。除此，三次函数的对称中心还有一个很少引起注意的性质---过三次曲线的对称中心且与该三次曲线相切的直线有且仅有一条；而过三次曲线上除对称中心外的任一点与该三次曲线相切的直线有二条.
由于三次曲线都是中心对称曲线，因此，将其对称中心移至坐标原点便可将三次函数的解析式简化为
。
若M（x1，y1）是三次曲线上的任一点，设过M的切线与曲线y=f（x）相切于（x0，y0），则切线方程为
，因点M上此切线上，故
，又
，所以
，整理得：
，解得，
或
。
综上所述，当点M是对称中心即
时，过点M作曲线的切线切点是惟一的，且为M，故只有一条切线；当点M不是对称中心即
时，过点M作曲线的切线可产生两个不同的切点，故必有两条切线，其中一条就是以M为切点（亦即曲线在点M处）的切线。
由此可见,不仅切线与曲线的公共点可以多于一个,而且过曲线上点的切线也不一定惟一。高中数学教材（不包括人民教育出版社中学数学室编著的《全日制普通高级中学教科书（试验修订本）》数学第三册（选修Ⅰ）（2001年12月版））只要求“某点处的切线”而没有提到“过某点的切线”，因此，也就不会涉及三次函数对称中心的这一性质。
深刻挖掘三次函数的性质，为高考有关问题找到了有效的解决方法，更为进一步探索高次函数的性质提供了方法依据.