垂直关系专题训练

垂直关系专题训练

1．（06江西卷）如图，在三棱锥A－BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD＝，BD＝CD＝1，另一个侧面是正三角形，求证：AD^BC

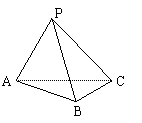
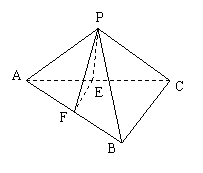2．（05辽宁卷）已知三棱锥Ｐ－ABC中，Ｅ、Ｆ分别是AC、AB的中点，△ABC，△PEF都是正三角形，PF⊥AB．证明PC⊥平面PAB

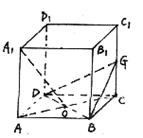
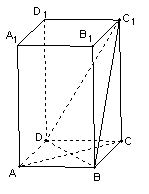
3. 在正方体ABCD—A₁B₁C₁D₁，G为CC₁的中点，O为底面ABCD的中心。

求证：A₁O⊥平面GBD

4. 已知直三棱柱ABC—A₁B₁C₁中，∠ACB=90⁰，∠BAC=30⁰，BC=1，AA₁=，M为CC₁中点，求证：AB₁⊥A₁M。

5. 已知矩形ABCD，过A作SA⊥平面AC，再过A作AE⊥SB交SB于E，过E作EF⊥SC交SC于F

(1)求证：AF⊥SC

(2)若平面AEF交SD于G，求证：AG⊥SD

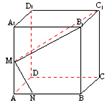
6. 如图，在正方体ABCD－A₁B₁C₁D₁中，M是棱A₁A的中点，N在AB上，且AN∶NB＝１∶３，求证：C₁M⊥MN．

7．正三棱柱ABC—A₁B₁C₁的侧面三条对角线AB₁、BC₁、CA₁中，AB₁⊥BC₁.求证：AB₁⊥CA₁.

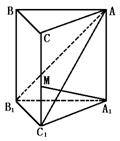
8．如图，已知直三棱柱ABC—A₁B₁C₁中，∠ACB＝90°，∠BAC＝30°，BC＝1，AA₁＝，M是CC₁的中点，求证：AB₁⊥A₁M.

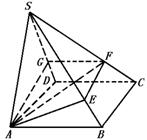
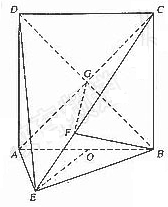
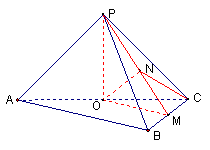
9．（06天津）如图，在五面体ABCDEF中，点O是矩形ABCD的对角线的交点，面CDE是等边三角形，棱

　 （I）证明平面

　 （II）设证明平面

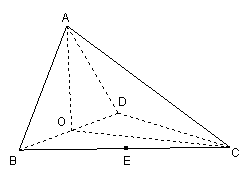10．（06福建卷）如图，四面体ABCD中，O、E分别是BD、BC的中点，

　 （I）求证：平面BCD；

　 （II）求点E到平面ACD的距离。

11．（05广东卷）如图3所示，在四面体中，已知，

．是线段上一点，，点在线段上，且．证明：；

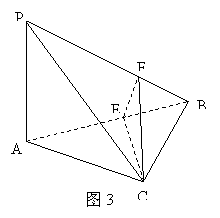
12．（05福建卷）如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.

（Ⅰ）求证AE⊥平面BCE；

（Ⅲ）求点D到平面ACE的距离.

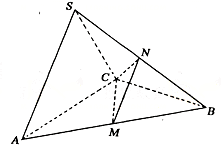
13. （04福建）在三棱锥S—ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2，M、N分别为AB、SB的中点.

（Ⅰ）证明：AC⊥SB；

（Ⅱ）求点B到平面CMN的距离.

14．（04全国Ⅱ）如图，直三棱柱ABC—A₁B₁C₁中，∠ACB=90°，AC=1，CB=，侧棱AA₁=1，侧面AA₁B₁B的两条对角线交点为D，B₁C₁的中点为M.求证CD⊥平面BDM；

15．（04全国Ⅲ）三棱锥中，侧面与底面垂直，

，求证：；

1．解：作AH^面BCD于H，连DH。

AB^BDÞHB^BD，又AD＝，BD＝1

\AB＝＝BC＝AC　\BD^DC

又BD＝CD，则BHCD是正方形，则DH^BC\AD^BC

方法二：取BC的中点O，连AO、DO

则有AO^BC，DO^BC，\BC^面AOD

\BC^AD

2．证明：连结CF.

，

∴

，

∴平面，

，

∴

∴平面

 

3．（I）证明：取CD中点M，连结OM。

　 在矩形ABCD中，

　 又

　 则连结EM，于是

　 四边形EFOM为平行四边形。

　

　 又平面CDE，且平面CDE，平面CDE。

　 （II）证明：连结FM。由（I）和已知条件，在等边中，

　 且

　 因此平行四边形EFOM为菱形，从而。

　 平面EOM，从而

　 而所以平面

4.解析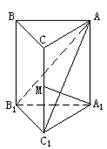：因结论是线线垂直，可考虑用三垂线定理或逆定理

∵ ∠ACB=90⁰

∴ ∠A₁C₁B₁=90⁰

即B₁C₁⊥C₁A₁

又由CC₁⊥平面A₁B₁C₁得：CC₁⊥B₁C₁

∴ B₁C₁⊥平面AA₁C₁C

∴ AC₁为AB₁在平面AA₁C₁C的射影

由三垂线定理，下证AC₁⊥A₁M即可

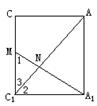在矩形AA₁C₁C中，AC=A₁C₁=，AA₁=CC₁=

∵ ，

∴

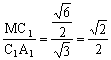∴ Rt△A₁C₁M∽Rt△AA₁C₁

∴ ∠1=∠2

又∠2+∠3=90⁰

∴ ∠1+∠3=90⁰_­

∴ AC₁⊥A₁M

∴ AB₁⊥A₁M

5．证明  (1)∵SA⊥平面AC，BC平面AC，∴SA⊥BC

∵矩形ABCD，∴AB⊥BC

∴BC⊥平面SAB

∴BC⊥AE又SB⊥AE　∴AE⊥平面SBC

∴SC⊥平面AEF

∴AF⊥SC

(2)∵SA⊥平面AC  ∴SA⊥DC，又AD⊥DC

∴DC⊥平面SAD　∴DC⊥AG

又由(1)有SC⊥平面AEF，AG平面AEF

∴SC⊥AG  ∴AG⊥平面SDC　∴AG⊥SD

6．证明１　设正方体的棱长为ａ，则MN＝，

C₁M＝，C₁N＝，

∵MN^２＋MC₁^２＝NC₁^２，∴C₁M⊥MN．

证明２　连结B₁M，∵C₁B₁⊥平面A₁ABB₁，

∴B₁M为C₁M在平面A₁ABB₁上的射影．

设棱长为a ，∵AN＝，AM＝，∴tan∠AMN＝，

又tan∠A₁B₁M＝，则∠AMN＝∠A₁B₁M，∴B₁M⊥MN，

由三垂线定理知，C₁M⊥MN．

7．如图，取A₁B₁、AB的中点D₁、P.连CP、C₁D₁、A₁P、D₁B，易证C₁D₁⊥平面AA₁B₁B.由三垂线定理可得AB₁⊥BD₁，从而AB₁⊥A₁D.再由三垂线定理的逆定理即得AB₁⊥A₁C.

8．解析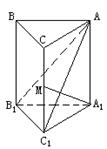：因结论是线线垂直，可考虑用三垂线定理或逆定理

∵ ∠ACB=90⁰

∴ ∠A₁C₁B₁=90⁰

即B₁C₁⊥C₁A₁

又由CC₁⊥平面A₁B₁C₁得：CC₁⊥B₁C₁

∴ B₁C₁⊥平面AA₁C₁C

∴ AC₁为AB₁在平面AA₁C₁C的射影

由三垂线定理，下证AC₁⊥A₁M即可

在矩形AA₁C₁C中，AC=A₁C₁=，AA₁=CC₁=

∵ ，

∴

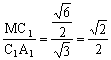∴ Rt△A₁C₁M∽Rt△AA₁C₁

∴ ∠1=∠2

又∠2+∠3=90⁰

∴ ∠1+∠3=90⁰_­

∴ AC₁⊥A₁M

∴ AB₁⊥A₁M

9．⑴证明：取AC中点O, 连结PO、BO.

∵PA＝PC　∴PO⊥AC　

又∵侧面PAC⊥底面ABC

∴PO⊥底面ABC

又PA＝PB＝PC　∴AO＝BO＝CO

∴△ABC为直角三角形　∴AB⊥BC

　

10．（I）证明：连结OC

　

　

　 在中，由已知可得

　 而 　 即

　 　 平面

　 （II）解：设点E到平面ACD的距离为

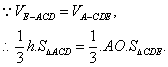　 　 在中，

　 　 而

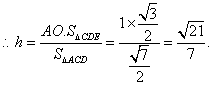
　 点E到平面ACD的距离为

11．证明：在中， ∵

　　　　　 ∴

　　　　 　　　 ∴△PAC是以∠PAC为直角的直角三角形，

同理可证，△PAB是以∠PAB为直角的直角三角形，

△PCB是以∠PCB为直角的直角三角形．

在中，∵

　　　　　　 ∴　 ∴

　　　　　　又∵

　　　　　　 ∴

12．解法一：(Ⅰ) ∵BF⊥平面ACE,∴BF⊥AE,∵二面角D-AB-E为直二面角,且CB⊥AB,

∴CB⊥平面ABE,∴CB⊥AE,∴AE⊥平面BCE

(Ⅱ)过E作EO⊥AB交AB于O,OE=1,∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.

设D到平面ACE的距离为h,∵,∴.

∵AE⊥平面BCE,∴AE⊥EC.∴h=.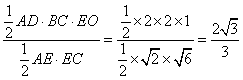

∴点D点D到平面ACE的距离为.

13．（Ⅰ）取AC中点D，连结SD、DB.

∵SA=SC，AB=BC，

∴AC⊥SD且AC⊥BD，

∴AC⊥平面SDB，又SB平面SDB，

∴AC⊥SB.

（Ⅱ）在Rt△NEF中，NF==，

∴S_△CMN=CM·NF=，S_△CMB=BM·CM=2.

设点B到平面CMN的距离为h，

∵V_B-CMN=V_N-CMB，NE⊥平面CMB，∴S_△CMN·h=S_△CMB·NE，

∴h==.即点B到平面CMN的距离为.

14．（Ⅰ）如图，连结CA₁、AC₁、CM，则CA₁=

　　 ∵CB=CA₁=，∴△CBA₁为等腰三角形，

又知D为其底边A₁B的中点，

　　 ∴CD⊥A₁B.　∵A₁C₁=1，C₁B₁=，∴A₁B₁=

　　 又BB₁=1，A₁B=2. ∵△A₁CB为直角三角形，D为A₁B的中点，

　　∴CD=A₁B=1，CD=CC₁，又DM=AC₁=，DM=C₁M.

　　∴△CDM≌△CC₁M，∠CDM=∠CC₁M=90°，即CD⊥DM.

　　因为A₁B、DM为平在BDM内两条相交直线，所以CD⊥平面BDM.

15．证明：取AC中点O, 连结PO、BO.

∵PA＝PC　∴PO⊥AC　

又∵侧面PAC⊥底面ABC

∴PO⊥底面ABC

又PA＝PB＝PC　∴AO＝BO＝CO

∴△ABC为直角三角形　∴AB⊥BC