高三12月份月考数学试卷(理)
一、选择题.(本大题共12题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1设全集U={2,4,6,8},集合A={2,m-6},![]() ,则m的值为
( )
,则m的值为
( )
A.2或-10 B.-10或-2 C.-2或10 D.2或10
2.已知向量![]() ,则m= (
)
,则m= (
)
A.![]() B.
B.![]() C.
C.![]() D.-
D.-![]()
3.已知![]() (
)
(
)
A.-3 B.3 C.![]() D.
D.![]()
4.若复数![]() 的实部与虚部是互为相反数,则b= (
)
的实部与虚部是互为相反数,则b= (
)
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
5.已知圆的半径为2,圆心在x轴的正半轴上,且与直线![]() 相切,则圆的方程是 (
)
相切,则圆的方程是 (
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.已知球O半径是1,A、B、C是球面上三点,且A与B、A与C、B与C的球面距离为![]() 则四面体OABC的体积为YCY (
)
则四面体OABC的体积为YCY (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若![]() =( )
=( )
A.550 B.1100 C.2050 D.2046
8.关于x的不等式![]() 的解集是空集,则a的取值范围是
( )
的解集是空集,则a的取值范围是
( )
A.(0,1) B.(-1,0) C.(1,2) D.(-∞,-1)
9.已知函数![]() (
)
(
)
A.2a2-M B.M-2a2 C.2M-a2 D.a2-2M
10.设双曲线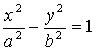 的右准线与两条渐近线交于A、B两点,右焦点为F,且
的右准线与两条渐近线交于A、B两点,右焦点为F,且![]() ,那么双曲线的离心率为 (
)
,那么双曲线的离心率为 (
)
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
11.某单位要从A、B、C、D四个人中选出三个人担任三种不同的职务,已知上届A、B、C三人任过这三种职务,这次不能连任原职,则不同的选法共有( )
A.10种 B.11种YCY C.12种 D.16种
12.已知![]() 是偶函数,
是偶函数,![]() ,若将
,若将![]() 的图象向右平移一个单位又得到一个奇函数,若
的图象向右平移一个单位又得到一个奇函数,若![]() (
)
(
)
A.-1003 B.1003 C.1 D.-1
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中的横线上)
13.若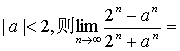 .
.
14.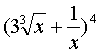 的展开式中的常数项为
.
的展开式中的常数项为
.
15.在直角坐标平面上,有两个区域P和Q,P是由y≥0,x-y≥0及x+y-2≤0三个不等式来确定的,Q是随m变化的区域,它由不等式m≤x≤m+1所确定,m的取值范围是0≤m≤1.设P和Q的公共面积是函数f(m),则f(m)= .
16.给出下面四个命题:
①过平面外一点,作与该平面成θ角的直线一定有无穷多条
②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行
③对确定的两异面直线,过空间任一点有且只有一个平面与两异面直线都平行
④对两条异面直线都存在无数多个平面与这两条直线所成的角相等
其中正确的命题序号为
一、选择题:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题:
1、 2、 3、 4、
三、解答题(本大题有6个小题;共74分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)YCY
从4名男生和2名女生中任选3人参加演讲比赛.
(Ⅰ)所选3人中至少有1名女生的概率;
(Ⅱ)设随机变量ξ表示所选3人中的女生人数.写出ξ的分布列要求出ξ的数学期望.
18.(本小题满分12分)
已知函数![]() .
.
(Ⅰ)求![]() 的最大值及最小值;
的最大值及最小值;
(Ⅱ)若又给条件q:“f(x)-m<2”且P是q的充分条件,求实数m的取值范围.
|
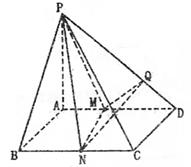
(Ⅰ)求证:平面PMN⊥平面PAD;
(Ⅱ)直线PC与平面PBA所成角的正弦值为![]() ,求PA的长;
,求PA的长;
(Ⅲ)求二面角P—MN—Q的余弦值.
20.(本小题满分12分)
已知函数![]() 的图象都相切,且
的图象都相切,且![]() 与函数f(x)图象的切点的横坐标为1.(Ⅰ)求直线l的方程及a的值;
与函数f(x)图象的切点的横坐标为1.(Ⅰ)求直线l的方程及a的值;
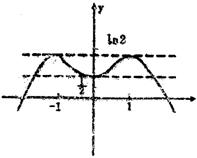
(Ⅱ)当k>0时,试讨论方程![]() 的解的个数.
的解的个数.
21.(本小题满分12分)
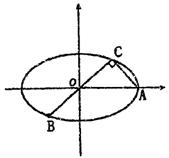
已知A、B、C是椭圆m: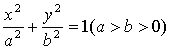 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为![]() ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且![]()
(Ⅰ)求椭圆m的方程;
(Ⅱ)过点(0,t)的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且![]() .求实数t的取值范围.
.求实数t的取值范围.
22.(本小题满分14分)
设函数![]()
(Ⅰ)求![]() 及定义域;
及定义域;
(Ⅱ)若数列![]() 的通项公式;
的通项公式;
(Ⅲ)Sn表示{bn}的前n项和,试比较Sn与![]() 的大小.
的大小.
高三数学(理科)参考答案
一、选择题
1—5 DBCCA 6—10 ADBAA 11—12 BD
二、填空题
13.1 14.108 15.![]() 16.②④
16.②④
三、解答题:
17.(Ⅰ)解:设所选三人中至少有1名女生的事件为A …………1分
P(A)=![]() …………4分
…………4分
(Ⅱ)ξ可能取的值为0,1,2, …………5分
P(ξ=k)=![]() k=0,1,2
…………8分
k=0,1,2
…………8分
ξ的分布列为
ξ 0 1 2
P
![]()
![]()
![]() …………10分
…………10分
∴Eξ=![]() ……………………12分
……………………12分
18.解:(Ⅰ)∵![]()
![]() …………3分
…………3分
又∵![]() …………4分
…………4分
即
![]() …………6分
…………6分
∴ymax=5, ymin=3
(Ⅱ)∵![]() …………9分
…………9分
又∵P为q的充分条件
∴![]() …………11分
…………11分
解得
![]() ………………12分
………………12分
19.解(Ⅰ)证明:∵PA⊥底面ABCD,MN![]() 底面ABCD
底面ABCD
∴MN⊥PA 又MN⊥AD 且PA∩AD=A
∴MN⊥平面PAD ………………3分
MN![]() 平面PMN ∴平面PMN⊥平面PAD …………4分
平面PMN ∴平面PMN⊥平面PAD …………4分
(Ⅱ)∵BC⊥BA BC⊥PA PA∩BA=A ∴BC⊥平面PBA
∴∠BPC为直线PC与平面PBA所成的角
即![]() …………7分
…………7分
在Rt△PBC中,PC=BC/sin∠BPC=![]()
∴![]() ………………9分
………………9分
(Ⅲ)由(Ⅰ)MN⊥平面PAD知 PM⊥MN MQ⊥MN
∴∠PMQ即为二面角P—MN—Q的平面角 …………11分
而![]()
∴![]() …………12分
…………12分
20.解(Ⅰ)由![]() ,故直线l的斜率为1,切点为
,故直线l的斜率为1,切点为![]()
即(1,0) ∴![]() ① ………………2分
① ………………2分
又∵![]()
∴![]() 即
即![]() ②…………4分
②…………4分
比较①和②的系数得![]() …………6分
…………6分
(Ⅱ)由![]()
设![]() …………8分
…………8分
![]()
令![]()
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
|
| + | 0 | - | 0 | + | 0 | - |
| y1 | ↗ | 极大值ln2 | ↘ | 极小值 | ↗ | 极大值ln2 | ↘ |
…………………………………………………………………………………………10分
|
(2)当![]() 时有3个解
时有3个解
(3)当![]() 时有4个解
时有4个解
(4)当k=ln2时有2个解
(5)当k>ln2时没有解 ………………12分
21.解(Ⅰ)∵![]() 过(0,0)
过(0,0)
则![]()
∴∠OCA=90°, 即![]() …………2分
…………2分
|
将C点坐标代入得 ![]()
解得 c2=8,b2=4
∴椭圆m:![]() …………4分
…………4分
(Ⅱ)由条件D(0,-2) ∵M(0,t)
1°当k=0时,显然-2<t<2 …………5分
2°当k≠0时,设![]()
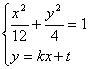 消y得
消y得
![]() …………7分
…………7分
由△>0 可得 ![]() ①………………8分
①………………8分
设![]()
则![]()
![]()
∴![]() …………10分
…………10分
由![]()
∴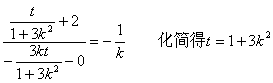 ②
②
∴t>1 将①代入②得 1<t<4
∴t的范围是(1,4)………………11分
综上t∈(-2,4) ………………12分
22.解(Ⅰ)由![]()
∵![]()
∴![]() …………2分
…………2分
∴![]() …………6分
…………6分
(Ⅱ)∵![]()
∴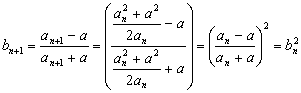 ………………8分
………………8分
∵![]() ∴
∴![]()
∴![]()
![]() ………………10分
………………10分
(Ⅲ)∴![]()
∵![]()
∴当![]()
![]() …………12分
…………12分
当![]()
当![]() 时,
时,![]()
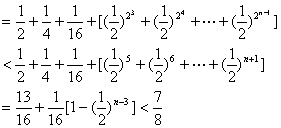
对于![]() ……………………14分
……………………14分