![]() 高三(上)期考数学试卷(文)
高三(上)期考数学试卷(文)
一、选择题:本大题共12小题,每小题5分,共60分.
![]()
 1.若集合
1.若集合![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]()
C. ![]() D.
D.![]()
2. 已知直线![]() ,直线
,直线![]() 与
与![]() 关于直线
关于直线![]() 对称,则直线
对称,则直线![]() 的斜率为
的斜率为
A.
![]() B.
B.![]() C.2 D.
C.2 D.![]()
3.关于两条直线![]() 与两个平面
与两个平面![]() ,有以下四个命题:
,有以下四个命题:
①若![]() 且
且![]() ,则
,则![]() ;
;
②若![]() 且
且![]() ,则
,则![]() ;
;
③若![]() 且
且![]() ,则
,则![]() ;
;
④若![]() 且
且![]() ,则
,则![]() ;
;
其中真命题的个数是
A. 1 B. 2 C. 3 D.4
4.如果实数![]() 满足
满足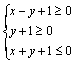 , 那么
, 那么![]() 的最大值为
的最大值为
A. 2
B.
1 C.
![]() D.
D.![]()
5.已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则![]() 的值为
的值为
A.5 B.4 C.3 D.1
6. 将函数![]() 的图像按向量
的图像按向量![]() 平移后,得到函数
平移后,得到函数![]() 的图像C,若曲线C关于原点对称,那么实数a 的值是
的图像C,若曲线C关于原点对称,那么实数a 的值是
A.-1 B.-3 C.0 D.1
7.设![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆上的点,且
是椭圆上的点,且![]() ,则
,则![]() 的面积是
的面积是
A 4 B 6 C ![]() D
D ![]()
8. .若![]() (
(![]() 为常数)在
为常数)在![]()
上是增函数,则m的取值范围是
A.
![]() B.
B.![]() C.
C.
![]() D.
D.![]()
9.设等差数列![]() 的前
的前![]() 项和是
项和是![]() ,且
,且![]() ,那么下列不等式中成立的是
,那么下列不等式中成立的是
A.![]() B.
B. ![]()
C.![]() D.
D.
![]()
10.![]() 的三内角
的三内角![]() 所对边长分别是
所对边长分别是![]() ,设
,设![]()
![]() ,
,
若向量![]() ,则角
,则角![]() 的大小为
的大小为
A.![]() B
B ![]() C.
C.![]() D.
D.![]()
11.若存在一个正数![]() ,使得函数
,使得函数![]() 对于定义域
对于定义域![]() 内任意两个不等的实数
内任意两个不等的实数![]() 都有:
都有:
![]() 成立,则称函数
成立,则称函数![]() 为
为![]() 上的利普希茨函数. 下列函数不能作为利普希茨函数的是
上的利普希茨函数. 下列函数不能作为利普希茨函数的是
A. ![]() B.
B.![]()
C. ![]() D.
D.![]()
12.已知![]() 是偶函数,当
是偶函数,当![]() 时,
时,
![]() 且当
且当![]() 时有
时有![]()
恒成立,则![]() 的最小值是
的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共4个小题,每小题4分,共16分;请将答案直接写在题中横线上.
13.一个容量为40的样本分成了5组,前3组的频数分别是4,7,11,第4组的频率是![]() ,那么第5组的频率是__▲____.
,那么第5组的频率是__▲____.
14.抛物线![]() 过焦点的弦
过焦点的弦![]() 的中点为
的中点为![]() ,则以弦
,则以弦![]() 为直径的圆的方程是____▲___
为直径的圆的方程是____▲___
15.将正奇数划分成下列组:(1),(3,5),(7,9, 11),
(13,15,17,19)…,则第n组各数的和是 ▲
16.下列命题正确的序号是____▲______
① 设非空集合![]() 满足
满足![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分非必要条件
”的充分非必要条件
②![]() 中,“
中,“![]() ”是“
”是“![]() 为锐角三角形” 的必要非充分条件
为锐角三角形” 的必要非充分条件
③“可导函数![]() 在
在![]() 处有极值”是“
处有极值”是“![]() ”的充分且必要条件
”的充分且必要条件
④![]() 是第一象限的角,则“
是第一象限的角,则“![]() ”是“
”是“![]() ”的非充分非必要条件.
”的非充分非必要条件.
答题卡:
| 题号 | 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. | 12. |
| 答案 |
13.________________; 14.__________________
15_________________; 16.___________________
三、解答题:本大题共6个小题,共74分;解答应写出文字说明、证明过程或演算步骤.
17.(12分)设函数![]() 的图象过点
的图象过点![]() 且
且![]() 的最大值是2,其中
的最大值是2,其中 ![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)设![]() ,求
,求![]() 的值。
的值。
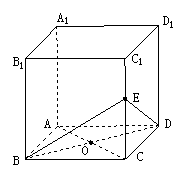
18. (12分)在正方体![]() 中,点
中,点![]() 在棱
在棱![]() 上,点
上,点![]() 为底面正方形的中心。
为底面正方形的中心。
(1)求证:![]() ;
;
(2)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证:![]() 面
面![]() ;
;
 (3)当
(3)当![]() 的值为多少时,
的值为多少时,![]() 面
面![]()
19. (12分)已知单调递增的等比数列![]() 满足
满足
![]() ,
,![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,求使
,求使![]() 成立的正整数
成立的正整数![]() 的最小值。
的最小值。
20. (12分)某地的一种农产品上市的时间仅能持续5个月,预计上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将供大于求而使价格连续下跌。现有三种价格模拟函数:①![]() ;
;
②![]() ;
;
③ ![]() 。(以上三式中
。(以上三式中![]() 均为常数,且
均为常数,且![]() ).
).
(1)为准确研究其价格走势,应该选择函数:
__________________.
(2)根据你所选择的函数![]() ,若
,若![]() ,求所选函数的解析式。 (注:函数的定义域为
,求所选函数的解析式。 (注:函数的定义域为![]() ,其中
,其中![]() 表示4月1日,
表示4月1日,![]() 表示5月1日,……,依此类推)
表示5月1日,……,依此类推)
(3)为保证农民的收益,政府打算在价格下跌时积极拓宽外销渠道。请你根据(2)的结果,预测该农产品在哪几个月内价格下跌?说明理由。
21. (12分)已知双曲线C:![]()
![]() 的离心率为
的离心率为![]() ,点
,点![]() 为该双曲线上的任意一点。
为该双曲线上的任意一点。
(1)若点![]() 到双曲线的两渐近线的距离分别为
到双曲线的两渐近线的距离分别为![]() ,求证:
,求证:![]()
(2)设直线![]() 与双曲线C交于A、B两点,F为右焦点,并且
与双曲线C交于A、B两点,F为右焦点,并且![]() ,求双曲线
,求双曲线![]() 的方程。
的方程。
![]() 22. (14分)已知函数
22. (14分)已知函数![]()
其中![]() 是以
是以![]() 为公差的等差数列,且
为公差的等差数列,且![]()
(1)设![]() 在
在![]() 处取极小值,试求当
处取极小值,试求当![]() 时
时![]() 的值.
的值.
(2)设![]() ,若
,若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,求
,求![]() 的值。
的值。
文科数学参考答案:
选择题:
| 题号 | 13. | 14. | 15. | 16. | 17. | 18. | 19. | 20. | 21. | 22. | 23. | 24. |
| 答案 | B | A | A | B | B | A | B | D | D | B | C | B |
填空题:
![]() ② ④
② ④
解答题:
17.(1)![]() ,
,![]() 的递增区间为:
的递增区间为:![]()
(2)
![]()
18.(3)当![]() 时,
时,![]() 平面
平面![]()
19.(1)设此等比数列为![]() 其中
其中![]() ,由条件求出
,由条件求出![]() 或
或![]() ,因为
,因为![]() 是单调递增的,所以
是单调递增的,所以![]() ,故
,故![]()
(2)![]() ,要使
,要使![]() 成立,即
成立,即![]() .
.![]() 函数
函数![]() 是单调递增的,且
是单调递增的,且![]() ,故
,故![]()
20.(1)选择函数![]() ;(2)
;(2)![]() ; (3)
; (3)![]() 知:在
知:在![]() 月份内价格下跌。
月份内价格下跌。
21.(2)由条件知双曲线方程为![]() ,
,![]() ,
, ,
,![]() 显然成立.设
显然成立.设![]() 则
则![]() ,
,![]()
![]()
![]()
带入整理得![]() , 所以双曲线方程为
, 所以双曲线方程为![]()
22.(1)
![]() ;又
;又![]() 或
或![]() ,由
,由![]() ,故当
,故当![]() 时
时![]() ;当
;当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 处取极小值,即
处取极小值,即![]()
(2)![]() ,
,![]() 的图像的开口向上,对称轴方程是
的图像的开口向上,对称轴方程是![]() ,由
,由![]() ,
,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,又由
,又由![]() 当
当![]() 时
时![]() 取最小值
取最小值![]() ,所以
,所以