高三春季招生考试数学试题(理工农医类)
一、选择题
（1）不等式组
的解集（ ）
（A）
（B）
（C）
（D）
（2）已知三条直线m、n、l，三个平面a、b、g，下列四个命题中，正确的是（ ）
（A）
（B）
（C）
（D）
（3）已知椭圆的焦点是
、
，
是椭圆上的一个动点．如果延长
到
，使得
，那么动点的轨迹是（ ）
（A）圆 （B）椭圆 （C）双曲线的一支 （D）抛物线
（4）如果
那么复数
的辐角的主值是（ ）
（A）
（B）
（C）
（D）
（5）若角
满足条件
，
，则在（ ）
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
（6）从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同工作．若其中甲、乙两名支援者都不能从事翻译工作，则选派方案共有（ ）
（A）280种 （B）240种 （C）180种 （D）96种
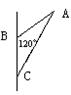
（7）在△
中，
，
，
（如图）．若将△绕直线
旋转一周，则所形成的旋转体的体积是（）
（A）
（B）
（C）
（D）
（8）（理）圆
与直线
(
,
,
)的位置关系是（ ）
（A）相交 （B）相切 （C）相离 （D）不能确定
（文）到两坐标轴距离相等的点的轨迹方程是（ ）
（A）
（B）
（C）
（D）
（9）（理）在极坐标系中，如果一个圆的方程
，那么过圆心且与极轴平行的直线方程是
（A）
（B）
（C）
（D）
（文）函数
的单调增区间是（ ）
（A）
() （B）
()
（C）
（） （D）
（）
（10）（理）对于二项式
，四位同学作出了四种判断：
①存在
，展开式中有常数项；②对任意，展开式中没有常数项；
③对任意，展开式中没有
的一次项；④存在，展开式中有的一次项．
上述判断中正确的是（ ）
（A）①与③ （B）②与③ （C）②与④ （D）①与④
（文）在
的展开式中，
的系数和常数项依次是（ ）
（A）20，20 （B）15，20 （C）20，15 （D）15，15
（11）若一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列有（ ）
（A）13项 （B）12项 （C）11项 （D）10项
（12）用一张钢板制作一个容积为
的无盖长方体水箱．可用的长方形钢板有四种不同的规格（长×宽的尺寸如各项所示，单位均为
）．若既要够用，又要所剩最少，则应选择钢板的规则是（ ）
（A）
（B）
（C）
（D）
二、填空题
（13）若双曲线
的渐近线方程为
，则双曲线的焦点坐标是 ．
（14）如果
，
，那么
的值等于______．
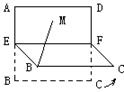（15）正方形
的边长是2，
、
分别是
和
的中点，将正方形沿
折成直二面角（如图所示）．
为矩形
内的一点，如果
，
和平面
所成角的正切值为
，那么点到直线的距离为_________．
（16）对于任意两个复数
，
（
为实数），定义运算
为：
．设非零复数
在复平面内对应的点分别为
，点O为坐标原点．如果
，那么在△
中，
的大小为________．
三、解答题
（17）在△中，已知
成等差数列，求
的值．
（18）已知
是偶函数，而且在
上是减函数．判断在
上是增函数还是减函数，并加以证明
（19）在三棱锥
中，
，
，
，
．
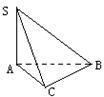（Ⅰ）证明：
^；
（Ⅱ）求侧面
与底面所成的二面角大小；
（Ⅲ）（理）求异面直线与所成的角的大小（用反三角函数表示）．
（文）求三棱锥的体积
．
（20）假设
型进口汽车关税税率在2001年是100﹪，在2006年是25﹪，2001年型进口车每辆价格为64万元（其中含32万元关税税款）．
（Ⅰ）已知与型车性能相近的
型国产车，2001年每辆价格为46万元．若型车的价格只受关税降低影响，为了保证2006年型车的价格不高于型车价格的90﹪，型车价格要逐年降低，问平均每年至少下降多少万元？
（Ⅱ）某人在2001年将33万元存入银行，假如该银行扣利息税后的年利率为1.8﹪（五年内不变），且每年按复利计算（例如，第一年的利息记入第二年的本金），那么五年到期时这笔钱连本带息是否一定够买一辆按（Ⅰ）中所述降价后的型汽车？
（21）（理）已知点的序列
，，其中
，
(
)，
是线段
的中点，
是线段
的中点，···，
是线段
的中点，···．
（Ⅰ）写出
与
之间的关系式 (
)；
（Ⅱ）设
，计算
，由此推测数列
的通项公式，并加以证明；
（Ⅲ）求
.
（文）已知某椭圆的焦点是
、
，过点并垂直于轴的直线与椭圆的一个交点为，且
，椭圆上不同的两点
、
满足条件：
、
、
成等差数列．
（Ⅰ）求该椭圆方程；
（Ⅱ）求弦
中点的横坐标；
（22）（理）已知某椭圆的焦点是、，过点并垂直于轴的直线与椭圆的一个交点为，且，椭圆上不同的两点、满足条件：、、成等差数列．
（Ⅰ）求该椭圆方程；
（Ⅱ）求弦中点的横坐标；
（Ⅲ）设弦的垂直平分线的方程为
，求的取值范围．
（文）已知点的序列，，其中， ()，是线段的中点，是线段的中点，···，是线段的中点，···．
（Ⅰ）写出与之间的关系式 ()；
（Ⅱ）设，计算，由此推测数列的通项公式，并加以证明；
（Ⅲ）求.