指数与指数函数
一、学习目标
1、理解n资助方根、根式、分数指数幂概念,会对根式、分数指数幂进行互化;
2、掌握分数指数幂的运算性质,熟练运用性质进行化简、求值;
3、培养化归意识,思维的灵活性和严密性;
4、掌握指数函数的根念;
5、掌握指数函数的图像、性质;
6、能利用指数函数的性质比较幂的大小;
7、培养学生的应用意识。
二、例题分析
第一阶梯
[例1]求下列各式的值;
![]()
![]()
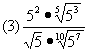
分析:
根式可化为分数指数幂形式,利用分数指数幂运算性质计算。
解:
![]()
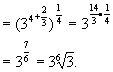
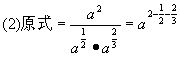
![]()
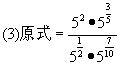
![]()
说明:
既含有分数指数幂,又有根式,一般把根式统一化成分数指数幂的形式,便于计算,如果根式中根
指数不同,也应化成分数指数幂的形式。
例2、指出下列函数中哪些是指数函数;
(1)y=4x; (2)y=x4;
(3)y=-4x; (4)y=(-4)x; (5)y=πx; ![]()
(7)y=xx;
分析:
根据指数函数定义进行判断。
解:(1)、(5)为指数函数;
(2)不是指数函数;
(3)是-1与指数函数4x的乘积;
(4)中底数-4<0,∴不是指数函数;
(6)中指数不是自变量x,而是x的函数x2;
(7)中底数x不是常数。
它们都不符合指数函数的定义。
说明:
指数函数严格限定在y=ax(a>0且a≠1)这一结构,(2)(3)(4)(6)(7)均不是指数函数,
不具备指数函数的基本性质。
第二阶梯
例3、
![]()
A、1 B、2a-1 C、1或2a-1 D、0
![]()
![]()
![]()
![]()
![]()
思路分析:
根据根式的意义直接进行判断.
解:
![]()
(2)取a=0,b=1,A不成立;取a=0,b=-1,C不成立;取a=-1,b=-1,D不成立;因为a2+b2≥0,所以B正确,
故选B.
答案:(1)C (2)B
例4、函数f(x)=x2-bx+c满足f(1+x)=f(1-x),且f(0)=3,则f(bx)与f(cx)的大小关系是_______。
思路分析:
利用二次函数、指数函数的单调性,结合函数的有关知识进行解答。
解答:
∵f(1+x)=f(1-x),∴f(x)的对称轴为x=1,由此得b=2,又∵f(0)=3,∴c=3.
∴f(x)=x2-2x+3在(-∞,1)内递减,在(1,+∞)内递增。
若x≥0,则3x≥2x≥1,∴f(3x)≥f(2x).
若x<0,则3x<2x<1, ∴f(3x)>f(2x).
即总有f(3x)≥f(2x),故应填f(cx)≥f(bx).
第三阶梯
例5、计算下列各式;
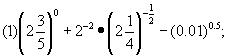
![]()
解:
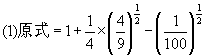
![]()
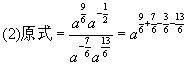
![]()
说明:
一般地,进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数为分数进行运算,
便于进行乘除、乘方、开方运算,以达到化繁为简的目的。
例6、
![]()
分析:
通过观察发现未知代数式中分子为立方和可分解为ax+ax与a2x-1+a-2x的积,化简约分即可将已知
代入求出结果,理解题意要注意从整体考虑。
解:
![]()
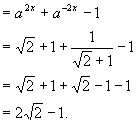
说明:
先化简后计算是代数运算的常用策略,要培养化简意识。
三、检测题
1、设0<a<b<1,则下列不等式正确的是( )
A、aa<bb B、ba<bb C、aa<ba D、bb<aa
2、已知0<a<1,b<-1,则函数y=ax+b的图像不经过( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
3、下列根式、分数指数幂的互化中,正确的是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
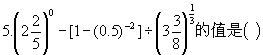
A、0 B、1/3 C、3 D、4
6.对任意实数x,下列等式正确的是( )
![]()
![]()
![]()
![]()
7、2-(2k+1)-2-(2k-1)+2-2k等于( )
A、2-2k B、2-(2k-1) C、-2-(2k+1) D、2
![]()
A.4x-5 B.-3 C.3 D.5-4x
9、若10x=3,10y=4,则10x-y=________________.
![]()
11、如果f(x)在区间[-2,4a-2a]上是奇函数,则a=_________.
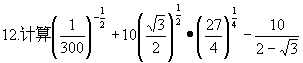
![]()
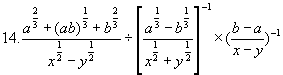
![]()
上的增函数。
答案:
1、C
2、A
3、C
4、C
5、C
6、C
7、C
8、C
![]()
![]()
11、1
![]()
![]()
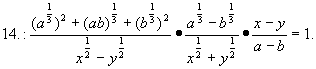
15、解:(1)奇函数;(2)(-1,1);(3)证略。