重点中学高三数学素质测试
数 学
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分,满分150分,考试时间120分钟.
第Ⅰ卷（选择题,共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选择项中，只有一项是符合题目要求的
1. 集合
，映射
满足
，那么映射的个数是 （ ）
A. 4 B. 5 C. 6 D. 7
2. 设
和
是互相垂直的单位向量，且
，则
等 （ ）
A. 1 B. 2 C. –1 D. –2
3. （文）已知实数
满足
，则下列不等式一定成立的是 （ ）
A. 
B. 
C. 
D. 
（理）若复数
满足
，则
的最小值是 （ ）
A. 1 B. 
C. 2 D.
4. 下列求导运算正确的是 （ ）
A. 
Ｂ. 
C. 
D. 
5. 设
是两条直线，
、
是两个平面，
为一点，有下列四个命题：①若
，
，则
与
必为异面直线；②若∥，∥则∥；③，
，∥，∥，则∥；④若
，，则
，其中正确命题的个数是 （ ）
A. 0 B. 1 C. 2 D.3
6. 如图：某电路中，在
、
之间有四个焊接点，若焊点脱落，则可能导致电路不通，今发现、
之间电路不通，则焊点脱落的不同情况有
（ ）
A. 4种 B. 10种 C.12种 D. 13种
7. 一个圆过抛物线
的顶点和该抛物线与直线
的两个交点，则当
趋于０时，圆心趋于 （ ）
A. 
B. 
C.
D. 
8. 实系数方程
的一个根大于０且小于１，另一个根大于１且小于２，则
的取值范围是 （ ）
A. 
B. 
C. 
D. 
9. 已知、是两条异面直线，直线
与、所成的角都是
，则与所成角的范围是
（ ）
A. 
B. 
C. 
D. 
10. 五个函数①
;②
;③
;④
;⑤
中，同时满足
的函数的序为 （ ）
A. ②③ B. ①④ C. ③④ D. ③⑤
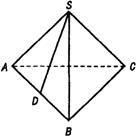
11. 在正三棱锥
－
中，
为
中点，且
与
所成角为
，则与底面所成角的正弦值为
（ ）
A. 
B. 
C. 
D. 
12. 过抛物线
的焦点
作一直线交抛物线于、两点，若线段
、
的长分别为
、
则
等于 （ ）
A. 
B. 
C. 
D. 
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上
13. 使方程
有解，取的取值范围是________.
14. 不等式
的解集是
，则不等式
的解集为
________.
15. 椭圆
的焦点为
、
，点
为椭圆上的动点，当 
时，点的横坐标的取值范围是________.
16. 给定
定义使
为整数的数
叫做企盼数，则区间
内的所有企盼数的和
________.
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤
17. （本小题满分10分）
已知
①若
，求
的单调增区间.
②若
时，的最大值为４，求的值.
③（理）在②的条件下，求满足
且
的
的集合.
18. （本小题满分12分）
5位同学各写一张贺卡放在一起，然后每人抽取一张贺卡
①恰好有3人抽到自己贺卡的概率是多少？
②至多有2人抽到自己贺卡的概率是多少？
19. （本小题满分12分）
长方体
中，
、分别是
、
的中点，
是
与
的交点.
①求二面角
－
－的正切值.
②求
值.
③三棱锥－
的体积.
20. （本小题满分12分）
某学生在体育训练时受了伤，医生给开了一些消炎药，并规定每天早晚八时各服一片，现知该药片每片含药量为220毫克，他的肾脏每12小时从体内滤出这种药的60％，若这种药在体内的残留量超过386毫克，就将产生副作用.
①该同学上午八时第一次服药，问到第二天上午八时服完药时，这种药在他体内还残留多少？
②若该同学长期服用这种药会不会产生副作用？
21. （本小题满分14分）
已知函数
是偶函数，
是奇函数，正数数列
满足
①求的通项公式；
②若的前项和为
，求
.
22. （本小题满分14分）
已知双曲线的渐近线为
，焦点在轴上，焦点到相应准线的距离为
.
①求此双曲线方程；
②设是双曲线的右焦点，、在双曲线上，且
，求直线的方程.
参考答案
1．D 2.C 3.文D，理A 4.B 5.A 6.D 7.A 8.A 9.B 10.C 11.C
12.B 13. [
14.文 
15. [
] 16.2026
17. （10分）解：（1）
…………………………文4分，理2分
的增区间为
…………………文6分，理4分
（2）易求出
上的最大值为
……………………文8分，理6分
……………………………………………………文10分，理8分
（3）
…………………………………………………………理10分
18.（12分）解：（1）
…………………………………………………………6分
（2）
………………………………………………………………12分
19．（12分）解：（1）
…………………………………………………………4分
（2）
…………………………………………………………8分
20．（12分）解：设该同学第次服药后，药在体内的残留量为
毫克.
…………………………………3分
……………………………………………………5分
（2）由
……………7分
是一个以数
为首项，0.4为公比的等比数列
………………………………………………9分
……………………………………………………………………11分
不会产生副作用……………………………………………………………………12分
21．（14分）解：（1）
为偶函数 
（2分）
为奇函数 
………………4分
…5分
…………………………………………………………………………8分
是以
为首项，公比为
的等比数列. 
………………10分
（2）
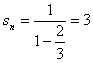…………………………………………………………14分
22．（14分）解：（1）
（7分） （2）
…14分