专题二数列复习测试卷（3）
一、选择题：
1．已知-9,a1,a2,-1这4个数成等差数列，-9,b1,b2,b3,-1 这5个数成等比数列，则b2(a2-a1)等于
A． 8 B． –8 C．
8
D． 
2．在数列{an}中，已知an+1=an+n（n∈N*），且a1=2，则a99的值是
A．1001 B．1001.5 C．1002 D．1002.5
3、等比数列{an}中，已知对任意自然数n，a1＋a2＋a3＋…＋an=2n－1，则
a12＋a22＋a32＋…+an2等于 ( )
A．
B．
C．
D． 
４．已知方程
的四个根组成的一个首项为
的等差数列，则 
（ ）（2003年全国理7）
A．1 B．
C．
D．
5．在等差数列
，则在Sn中最大的负数为 （ ）
A．S17 B．S18 C．S19 D．S20
6．已知等差数列
与等比数列
的首项均为1，且公差d
1，公比q＞0且q1，则集合
的元素最多有 （ ）
A．1个 B．2个 C．3个 D．4个
7、已知
，（
），则在数列｛
｝的前50项中最小项和最大项分别是（ ）
A．
B．
C．
D．
8.数列1，1+2，1+2+22，…，1+2+22+…+2n－1，…的前n项和为（ ）
A.2n－n－1 B.2n+1－n－2 C.2n D.2n+1－n
9．已知数列的通项公式为
，则该数列的前n项的和为 ( )
A. 
B. 
C.
D. 
10．已知
和
成等差数列，而
成等比数列，且
，则
的值为
A.1 B.2 C.3 D.4
11. 数列｛an｝中，
，若sn = 9 ，则n等于
（ ）
A. 9 B. 10 C. 99 D. 100
二、填空题：
13.等比数列{an} 中，
，
,则
14.数列
的前n项和为
,则
=
15.已知
(n∈N*),则数列{an}的最大项为_______.
16.若{an}是递增数列λ对于任意自然数n,
恒成立， 求实数λ的取值范围是
三、解答题：
17.（本小题满分10分）已知等差数列{an}中，a2=8,前10项和S10=185.
（1）求通项；
（2）若从数列{an}中依次取第2项、第4项、第8项…第2n项……按原来的顺序组成一个新的数列{bn}，求数列{bn}的前n项和Tn.
18．（2003年天津文19）已知数列
（Ⅰ）求
（Ⅱ）证明
19.（本小题满分10分）已知y=f(x)为一次函数，且f(2)、f(5)、f(4)成等比数列，f(8)=15,求Sn=f(1)+f(2)+…+f(n)的表达式.
20. 数列{an}的前n项和为
（1）求通项an；
（2）是否存在常数a、b，使得对一切自然数n都有
成立.若存在，
求出a、b的值；若不存在，说明理由.
21.设数列{}的首项
=1前n项和
满足关系式
(t>0,n∈N,n≥2)．
（1） 求证数列{}是等比数列；
（2） 设数列{}的公比为
，作数列{
}，使
，
，(n∈ N,n≥2)，求bn．
22.数列｛an｝满足a1=1,an=
an-1+1 (n≥２)
⑴ 写出数列｛an｝的前５项；
⑵ 求数列｛an｝的通项公式。
答 案
1.C 3.D 4C 5.C 6.B 7.C 8. B 9. C
10. B 11.C
3.在等比数列{an}中，已知n∈N*,且a1+a2+…+an=2n－1,那么a12+a22+…+an2等于（ ）
(A) (B) (C)
(D)
考查等比数列概念、求和.
【解析】 由Sn=2n－1,易求得an=2n－1,a1=1,q=2,∴{an2}是首项为1，公比为4的等比数列，由求和公式易知选B.
【答案】 B
8考查一般数列求和的技巧.
【解析】 an=2n－1,∴Sn=(2+22+…+2n)－n=2n+1－n－2.
【答案】 B
9. 选 C ( 利用错位相减法)
二、填空题：
13. 190
14.
15．【解析】 设{an}中第n项最大，则有
即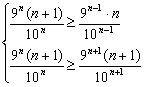
,∴8≤n≤9
即a8、a9最大.
【答案】 a8和a9
16.考查数列和不等式基本知识.
【解析】 因为{an}为递增数列，∴n2+λn>(n－1)2+λ(n－1)(n≥2)
即2n－1>－λ(n≥2)
λ>1－2n(n≥2)
要使n∈N*恒成立，则λ>－3.
【答案】 λ>－3
三、解答题：
17.（本小题满分10分）已知等差数列{an}中，a2=8,前10项和S10=185.
（1）求通项；
（2）若从数列{an}中依次取第2项、第4项、第8项…第2n项……按原来的顺序组成一个新的数列{bn}，求数列{bn}的前n项和Tn.
考查等差、等比数列性质、求和公式及转化能力.
【解】 （1）设{an}公差为d,有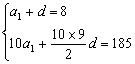
解得a1=5,d=3
∴an=a1+(n－1)d=3n+2
(2)∵bn=a
=3×2n+2
∴Tn=b1+b2+…+bn=(3×21+2)+(3×22+2)+…+(3×2n+2)=3(21+22+…+2n)+2n=6×2n+2n－6.
18． （Ⅰ）∵a1=1 . ∴a2=3+1=4, a3=32+4=13 .
（Ⅱ）证明：由已知an－an－1=3n－1,故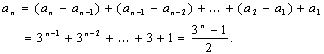
所以证得
19.（本小题满分10分）已知y=f(x)为一次函数，且f(2)、f(5)、f(4)成等比数列，f(8)=15,求Sn=f(1)+f(2)+…+f(n)的表达式.
考查用函数的观点认识数列的能力及等比数列的求和.
【解】 设y=f(x)=kx+b,则f(2)=2k+b,f(5)=5k+b,f(4)=4k+b,依题意：［f(5)］2=f(2)·f(4).
即(5k+b)2=(2k+b)(4k+b)化简得k(17k+4b)=0.
∵k≠0,∴b=－
k ①
又∵f(8)=8k+b=15 ②
将①代入②得k=4,b=－17.
∴Sn=f(1)+f(2)+…+f(n)=(4×1－17)+(4×2－17)+…+(4n－17)=4(1+2+…+n)－17n=2n2－15n.
20. 数列{an}的前n项和为
（1）求通项an；
（2）是否存在常数a、b，使得对一切自然数n都有成立.若存在，
求出a、b的值；若不存在，说明理由.
解：①
②假设存在这样的a,b，使得对一切自然数n都有
则
令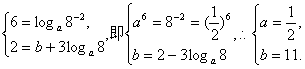
∴存在这样的数
21. 分析 由已知等式作递推变换，转化为关于
与的等式，在此基础上分析
与的比值，证得（1）的结论后，进一步求，再分析数列{}的特征，并求其通项公式．
（1）证明：由
=1，
，
，得
， 于是
．
……①
又，
（n=3,4，……），
两式相减，得
，
即
．
于是，得
（n=3,4……）．
……②
综合①②，得是首项为1，公比为
的等比数列．
（2）解 由（1），得
，
即
．
所以数列
是首项为1，公差为
的等差数列，于是
．
点评 要判断一个数列是否是等比数列，关键要看通项公式，若是已知求和公式，在求通项公式时一方面可用
，另一方面要特别注意是否符合要求．
22. 数列｛an｝满足a1=1,an=an-1+1 (n≥２)
⑴ 写出数列｛an｝的前５项；
⑵ 求数列｛an｝的通项公式。
分析 写出数列｛an｝的前５项，可猜想an，在此基础上，可对递推公式作相应变形。也可依据递推公式，从特殊情况向一般情况递推，并将迭代法与累加法相结合，求an.
其它常规方法较多，不作一一分析。
解 ⑴ a1=1 ,a2=
（ 猜想 
｛an-2｝是等比数列 ）
⑵
解法一 由an=an-1+1 (n≥２) 得
an－2=(an-1－2) 令 bn= an－2 则bn=bn-1
又b1=a1－2=-1 故 bn=
于是 an=2
解法二
由an=an-1+1， 得 an-1=an-2+1 。
⑴－⑵，得an－an-1= (an-1－an-2) 。 由此递推，可得
an－an-1=（）n-2=()n-1，
an-1－an-2=（）n-2，
…………
a2－a1=。
上述n-1个等式相加得
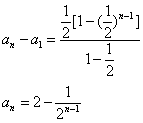
解法三 设 an+k=h(an-1+k)其中k、h为待定系数。
将an=han-1+kh-k 与 an=an-1+1
比较得 h= , k=－2
故an－2=(an-1－2) (n≥２) 而 a1－2=－1
数列｛an－2｝是以 为公比，－1首项的等比数列。
an－2=， an=2。
点评 以上三种解法，对递推公式只涉及相邻两项的情况均适合，特别是解法三较简便，应予以巩固。对于各种解法中用到的归纳、猜想、递推、待定系数法等思想方法，要用心体会。