高三年级第一次月考数学试卷
总分150分
一、选择题(5/×10=50/)
1.设全集![]() ,集合
,集合![]() ,
,![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.φ
D.φ
2.函数![]() 的定义域为R,若
的定义域为R,若![]() ,
,![]() ,则
,则![]()
A. 1
B.![]() C.
C.![]() D.
D. ![]()
3.函数![]() ,则
,则![]() 的值为
的值为
A.0 B.- 1 C.1 D.±1
4.若![]() ,且
,且![]() ,则角
,则角![]() 的终边位于
的终边位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.已知函数![]() ,则
,则![]()
A.-2 B. 2 C. 0 D.-1
6.设![]() ,且
,且![]() ,则
,则![]()
A.-7 B. 7 C.17 D.-17
7.
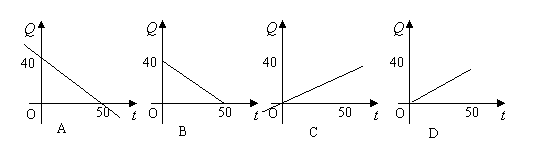 一水池蓄水40m3,从一管道等速流出,50min流完,则水池的剩余水量Q(m3)与流出时间t(min)的函数关系图象可表示为
一水池蓄水40m3,从一管道等速流出,50min流完,则水池的剩余水量Q(m3)与流出时间t(min)的函数关系图象可表示为
8.函数![]() 的图象经过点(0,1),则函数
的图象经过点(0,1),则函数![]() 的反函数的图象经过点
的反函数的图象经过点
A.(3,0) B.(0,3) C.(4,1) D.(1,4)
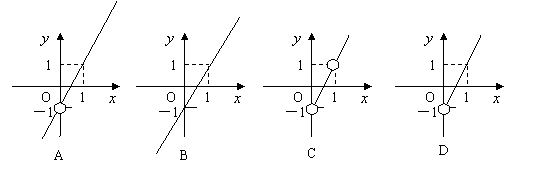 9.下列图形中,方程
9.下列图形中,方程![]() 对应的图形是
对应的图形是
10.如果函数![]() 对
对![]() 均有
均有![]() ,那么
,那么
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(5/×4=20/)
11.若函数![]() (
(![]() )满足
)满足![]() ,且
,且![]() 时,
时,![]() 。则函数
。则函数![]() 的图象与函数
的图象与函数![]() 的图象的交点的个数为6。
的图象的交点的个数为6。
12.已知函数![]() ,当
,当![]() 时为增函数,在
时为增函数,在![]() 时为减函数,则
时为减函数,则![]() 13。
13。
13.若函数![]() 是奇函数,且当
是奇函数,且当![]() 时
时![]() 为增函数,
为增函数,![]() ,又
,又![]() ,则不等式
,则不等式![]() 的解集为
的解集为![]() 。
。
14.已知定义在R上的函数![]() 满足
满足![]() ,则
,则![]() 7。
7。
数学试卷答题卷
| 题号 | 一 | 二 | 15 | 16 | 17 | 18 | 19 | 20 | 总分 |
| 得分 |
一、选择题(5/×10=50/)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 得分 |
| 答案 | B | C | C | B | A | D | B | D | C | A |
二、填空题(5/×4=20/)
11. 6 ; 12. 13 ; 13.![]() ;14.7;
;14.7;
三、解答题(本题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)
15.(满分12分) 已知函数![]() 。
。
(1)若![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
解:当![]() ,即
,即![]() 或
或![]() ;
;
![]() 时
时![]() ,不符合题意,所以
,不符合题意,所以![]() ;
;
![]() 时,
时,![]() ,定义域为R;
,定义域为R;
当![]() ,则
,则
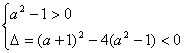 ,即
,即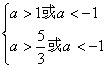 ,所以
,所以![]() 。
。
综上![]()
(2)若![]() 的值域为
的值域为![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
依题意,只要![]() 能取到
能取到![]() 上任何值,则
上任何值,则![]() 的值域为R,故
的值域为R,故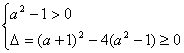 ,解得
,解得![]()
又当![]() ,即
,即![]() 时
时![]() 符合题意,
符合题意,![]() 是不符合题意,所以
是不符合题意,所以![]()
16.(满分14分)若![]() ,
,![]() ,且A=B,
,且A=B,![]() 。
。
(1)求![]() 零点个数;
零点个数;
∵A=B,
∴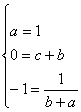 ,∴
,∴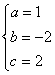 ,∴
,∴![]()
又![]() ,所以
,所以![]() 没有零点。
没有零点。
(或因为![]() ,所以
,所以![]() 没有零点。)
没有零点。)
(2)当![]() 时,求
时,求![]() 的值域;
的值域;
因为![]() 的对称轴
的对称轴![]() ,所以当
,所以当![]() 时
时
![]() ,
,![]() ,
,
∴![]() 。
。
(3)若![]() 时,
时,![]() ,求m的值。
,求m的值。
∵![]() 在
在![]() 上为增函数,
上为增函数,
∴![]()
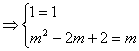 ∴
∴![]() 或
或![]() ,又
,又![]() ,所以
,所以![]() 。
。
17.(满分14分)已知函数![]() 。
。
(1)判断![]() 的奇偶性,并加以证明;
的奇偶性,并加以证明;
![]() 为奇函数。
为奇函数。
因为![]() 的定义域为R,对
的定义域为R,对![]()
∵![]() ,
,
∴![]() 为奇函数。
为奇函数。
(2)判断![]() 的单调性,并加以证明;
的单调性,并加以证明;
![]() 是
是![]() 上的增函数。
上的增函数。
∵对![]() ,
,![]() ,
,![]()
又![]()
![]() ;
;
∴![]() 是
是![]() 上的增函数。
上的增函数。
方法2:利用导数。
(3)求![]() 的值域;
的值域;
∵![]() ,又
,又![]() 是
是![]() 上的增函数,
上的增函数,
∴![]() 。
。
(4)解不等式![]() 。
。
∵![]() ;
;
又∵![]() 即为
即为![]() ;
;
又![]() 是
是![]() 上的增函数;
上的增函数;
∴不等式![]() 的解集为
的解集为![]()
方法2:解![]() 得
得![]() 则
则![]()
∴不等式![]() 的解集为
的解集为![]() 。
。
18.(满分12分)已知函数![]() ,将函数
,将函数![]() 的图象向左平移2个单位,再向上平移1个单位,就得到
的图象向左平移2个单位,再向上平移1个单位,就得到![]() 的图象。
的图象。
(1)写出![]() 的解析式;
的解析式;
解:∵![]() ;∴
;∴![]() ;则向左平移2个单位,再向上平移1个单位,得到
;则向左平移2个单位,再向上平移1个单位,得到![]() ,∴
,∴![]() ,即
,即
![]() (
(![]() )。
)。
(2)求出![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值。
的值。
∵![]() ;
;
∴![]()
![]()
当且仅当![]() 即
即![]() 舍去)时,
舍去)时,![]() 。
。
19.(满分14分)已知函数![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 在
在![]() 上是
上是![]() 的一次函数,在
的一次函数,在![]() 上是
上是![]() 的二次函数,且当
的二次函数,且当![]() 时,
时,![]() ,
,![]() ,求
,求![]() 的解析式。
的解析式。
解:∵![]() 在
在![]() 上是
上是![]() 的二次函数,且当
的二次函数,且当![]() 时,
时,![]() ;
;
∴(5,3)是此二次函数图象的顶点,设这个二次函数为![]() 。
。
∵![]() ;
;
∴![]() 。
。
∴![]() (
(![]() ),∴
),∴![]() 。
。
又函数![]() 是定义在
是定义在![]() 上的奇函数;
上的奇函数;
∴![]() 。
。
∵![]() 在
在![]() 上是
上是![]() 的一次函数,且
的一次函数,且![]() ,
,![]() ;
;
∴![]() 。
。
又∵函数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
∴![]() 时,
时,![]() ;
;
![]() 时,
时,![]() 。
。
综上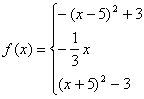
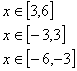
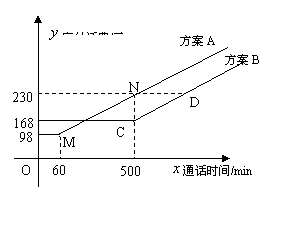 20.(满分14分)电信局为了配合客户不同需要,设有A,B两种优惠方案。这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD。
20.(满分14分)电信局为了配合客户不同需要,设有A,B两种优惠方案。这两种方案应付话费(元)与通话时间(min)之间的关系如图所示,其中MN∥CD。
(1)若通话时间为2小时,按方案A,B各付话费多少元?
(2)方案B从500min以后,每分钟收费多少元?
(3)通话时间在什么范围内,方案B比方案A优惠?
解:设这两种方案的应付话费一通话时间的函数关系分别为![]() 和
和![]() ,由图知M(60,98),N(500,230),C(500,168),MN∥CD; 则
,由图知M(60,98),N(500,230),C(500,168),MN∥CD; 则
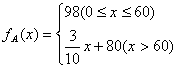 ;
;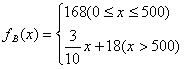 。
。
(1)通话2小时的费用分别是116元、168元。
(2)∵![]() ;
;
∴方案B从500min以后,每分钟收费0.3元。
(3)由图知,当![]() 时,
时,![]() ;
;
当![]() 时,由
时,由![]() 得
得![]() ;
;
当![]() 时
时![]() 。
。
综上,通话时间在![]() 内,方案B比方案A 优惠。
内,方案B比方案A 优惠。