高三年级第一学期第三次月考数学试题
总分150分
第一卷（客观题）
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）：
1．已知等差数列
的公差为2，若
成等比数列，则
（ ）
A．
B．
C．
D．
2．设函数
的最小值
，最大值
，记
则
是 （ ）
A．公差不为0的等差数列 B．公比不为1的等比数列
C．常数列 D．不是等差也不是等比数列
3．在各项为正数的等比数列中，
，则
= （ ）
A．33 B．72 C．84 D．189
4．若数列的前n项和
，则
（ ）
A．
B．
C．
D．
5．在数列中，
，且
则数列的第10项为 （ ）
A．
B．
C．
D．
6．已知
，则数列的通项公式
（ ）
A．
B．
C．
D．
|
中，第n项到n+6项的和为
，则当
最小时，n的值为
（ ）
A．6 B．4 C．5 D．3
8．已知等比数列中，
则
（ ）
A．－2 B．－5 C．2或－5 D．2
9．设Sn是等差数列的前n项和，
则
（ ）
A．21 B．16 C．9 D．8
10．已知数列的通项公式
，设前n项和为Sn，则使
成立的自然数n （ ）
A．有最大值63 B．有最小值63 C．有最小值31 D．有最大值31
11．数列Sn是满足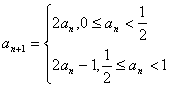
，若
，则
的值为 （ ）
A．
B．
C．
D．
12．若等比数列的各项均为正数，前n项和为S，前n项积为P，前n项的倒数和为M，则
（ ）
A．
B．
C．
D．
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在横线上）：
13．在数列中
，且
则
.
14．数列满足
则的通项公式是
.
15．已知等比数列中，
且
则
的取值范围是
.
16．设等比数列的公比为q，前n项和为Sn，若
成等差数列，则q的值为
.
第二卷（主观题）
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）：
17．（12分）在等比数列中，
且公比q是整数。
求
的值
18．（12分）从1，2，3，4，5，6这6个数中任取两个不同的数作差
|
，求的分布列及期望。
（文）（1）记“事件A”=差的绝对值等于1，求P（A）；
（2）记“事件B”=差的绝对值不小于3，求P（B）。
19．（12分）有个正数排成n行n列方陈（
）如图：
…
………
其中每行数成等差数列，第一列数成等比数列且公比都等于q，设
（1）求公比q；
（2）求
；
（3）求
|
20．（12分）定义在R上的函数
的图象关于
对称，且满足
又
求
。
21．（12分）（理）已知数列相邻两项
是方程
的两根
且
，求与
。
（文）已知
又
是一个递增等差数列的前3项
（1）求此数列的通项公式；
（2）求
的值。
22．（14分）已知数列中
，且
在直线
上，
（1）求数列的通项公式；
（2）若
，求Tn的最小值；
（3）若
是
的前n项和，问：是否存在关于n的整式
使得
对一切
的自然n恒成立说明理由。
参 考 答 案
第一卷（客观题）
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | D | D | D | C | D | A | B | C | C |
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在横线上）：
13．2600
14．
15．
16．
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）：
17．
18．
|
| 1 | 2 |
| 4 | 5 | ||
| P | 1/3 | 4/15 | 3/15 | 2/15 | 1/15 |
（文）P（A）=1/3，P（B）=2/5
19．（1）
（2）
（3）
20．
|
|
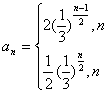
（文）
22．（1）
（2）的最小值为
（3）存在，