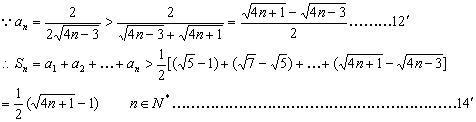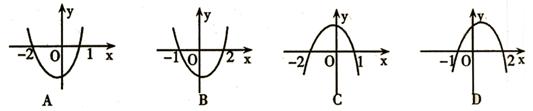高三年级第一学期期中考试数学试题(理科)
说明:本试题分为第Ⅰ卷和第Ⅱ卷两部分.共150分,考试时间120分钟.
第I卷
一、选择题:共12小题每小题5分,满分60分,在每小题给出的四个选项中,只有一个选项是符合题目要求的,把正确的选项的代号涂在答题卡上.
1.设集合![]() ( )
( )
A.![]() B.[-2,0] C.[0,2] D.
B.[-2,0] C.[0,2] D.![]()
2.已知向量![]() 的值为 ( )
的值为 ( )
A.0 B.2 C.4 D.8
3.已知函数![]() 的解集为(-2,1)则函数
的解集为(-2,1)则函数![]() 的图象为
的图象为
( )
|
4.如果不等式组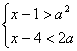 有解,则实数a的取值范围是 ( )
有解,则实数a的取值范围是 ( )
A.(-∞,-1)∪(3,+∞) B.(-∞,-3)∪(1,+∞)
C.(-1,3) D.(-3,1)
5.等差数列{an}中,a1+a4+a7=39, a3+a6+a9=27,则数列{an}前9项的和S9等于 ( )
A.66 B.99 C.144 D.297
6.已知函数![]() 在区间[0,t]上至少取得2个最大值,则正整数t的最小值是( )
在区间[0,t]上至少取得2个最大值,则正整数t的最小值是( )
A.8 B.9 C.10 D.11
7.设函数![]() 的前n项和是
的前n项和是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知正数![]() 的最小值是9,则正数a的值是 ( )
的最小值是9,则正数a的值是 ( )
A.1 B.2 C.4 D.8
9.函数![]() 的单调递减区间是 ( )
的单调递减区间是 ( )
A.(![]() ,+∞) B.(-∞,
,+∞) B.(-∞,![]() ) C.(0,
) C.(0,![]() ) D.(e,+∞)
) D.(e,+∞)
10.函数![]() 的定义域为[a,b],值域为[0,2]则b-a的最小值是 ( )
的定义域为[a,b],值域为[0,2]则b-a的最小值是 ( )
A.![]() B.3 C.
B.3 C.![]() D.2
D.2
11.在等比数列{![]() }中,a1=2,前n项和为Sn,若数列{
}中,a1=2,前n项和为Sn,若数列{![]() +1}也是等比数列,则Sn等于( )
+1}也是等比数列,则Sn等于( )
A.2n+1-2 B.3n C.2n D.3n-1
12.已知![]() =
=
( )
A.![]() B.-
B.-![]() C.-
C.-![]() 或
或![]() D.0或-
D.0或-![]()
二、填空题:本大题有4个小题,每小题4分,共16分;将答案填写在第II卷相应的题号后面的空格内.
13.已知x、y满足约束条件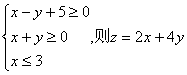 的最小值为
.
的最小值为
.
14.若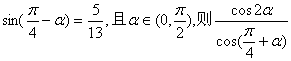 值为
.
值为
.
|
程是![]() =
.
=
.
16.有两个向量![]() =(1,0),
=(1,0),![]() =(0,1),今有动
=(0,1),今有动
点P从P0(-1,2)开始沿着与向量![]() +
+![]() 相同
相同
的方向作匀速直线运动,速度为![]() +
+![]() ;另一动点Q从Q0(-2,-1)开始沿着与向量3
;另一动点Q从Q0(-2,-1)开始沿着与向量3![]() +2
+2![]() 相同的方向作匀速直线运动,速度为3
相同的方向作匀速直线运动,速度为3![]() +2
+2![]() .设P、Q在时刻t=0秒时分别在P0、Q0处,则当
.设P、Q在时刻t=0秒时分别在P0、Q0处,则当![]() 时,t=
秒.
时,t=
秒.
第Ⅱ卷
三、解答题:本大题共6个小题,满分74分,解答时要求写出必要的文字说明或推演步骤.
17.(本题满分12分)
在△ABC中,角A、B、C所对的边分别是a、b、c,若sin2B+sin2C=sin2A+sinBsinC,且![]() ,求△ABC的面积S.
,求△ABC的面积S.
18.(12分)已知![]() 、
、![]()
![]()
(1)求向量![]() ;
;
(2)求![]() 、
、![]() 的值.
的值.
19.(12分)已知函数![]() 的图象关于原点对称.
的图象关于原点对称.
(1)写出y=g(x)的解析式;
(2)若函数F(x)=f(x)+g(x)+m为奇函数,试确定实数m的值;
(3)当![]() 成立,求 实数n的取值范围.
成立,求 实数n的取值范围.
20.某企业实行裁员增效,已知现有员工a人,每人每年可创纯利润1万元,据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的![]() ,设该企业裁员x人后纯收益为y万元.
,设该企业裁员x人后纯收益为y万元.
(1)写出y关于x的函数关系式,并指出x的取值范围;
(2)当140<a≤280时,问该企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得大经济效益的情况下,能少裁员,应尽量少裁)
21.(12分)已知![]()
(1)当a=1时,求f(x)的单调区间;
(2)是否存在实数a,使f(x)的极大值为3?若存在,求出a的值,若不存在,请说明理由.
22.(14分)已知:![]() 在曲线
在曲线
![]()
(1)求数列{an}的通项公式;
(2)数列{bn}的前n项和为Tn,且满足![]() ,设定b1的值,使得数列{bn}是等差数列;
,设定b1的值,使得数列{bn}是等差数列;
(3)求证:![]()
参考答案及评分标准
一、选择题
BCDCB DABCC CD
二、填空题
13.-6 14.![]() 15.2 16.2
15.2 16.2
三、解答题
17.解:由已知得![]() ……………………………………2′
……………………………………2′
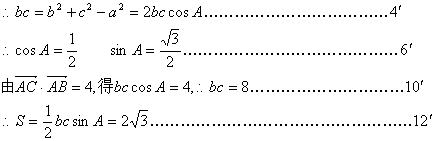
18.解:(1)![]() ……………………1′
……………………1′
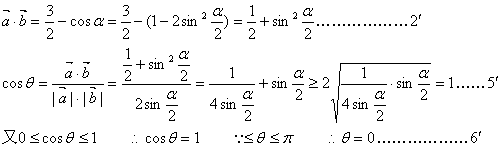
(2)由(1)可知,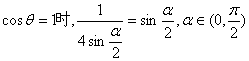 ……………………8′
……………………8′
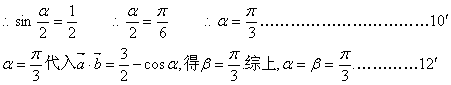
19.解:(1)设M(x,y)是函数y=g(x)图象上任意一点,
则M(x,y)关于原点的参考消息称点为N(-x,-y)
N在函数![]() …3′
…3′
(2)![]() 为奇函数.
为奇函数.
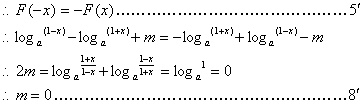
(3)由![]()

20.解:(1)![]()
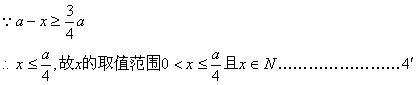
(2)![]() …………………………6′
…………………………6′

21.解:(1)当![]() ……2′
……2′
![]()
∴f(x)的单调递增区间为(0,1),单调递减区间(-∞,0)(1,+∞)…4′
(2)![]() ………………6′
………………6′
令![]()
列表如下:
| x | (-∞,0) | 0 | (0,2-a) | 2-a | (2-a,+ ∞) |
| f′(x) | - | 0 | + | 0 | - |
| f(x) |
| 极少 |
| 极大 |
|
由表可知,![]() ……………………………………8′
……………………………………8′
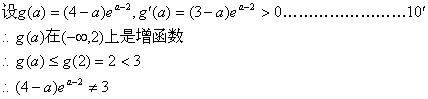
∴不存在实数a,使f(x)最大值为3.………………………………………………12′
22.解:(1)由于![]()
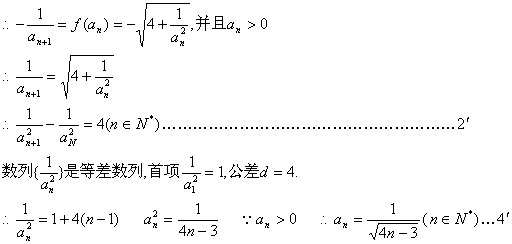
(2)![]()
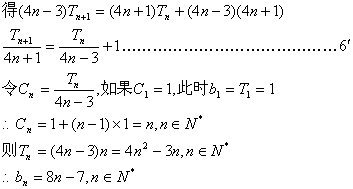
此时数列{bn}是等差数列……………………………………………………10′
(3)![]()