高三年级第一学期期中考试数学试题
命题、审阅：王家清
总分１５０分
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的，把答案填写在答题卷相应位置上。
B 1．命题“x∈M或x∈P”是“x∈M∩P”的
（A）充分非必要条件 （B）必要非充分条件
（C）充要条件 （D）既不充分也不必要条件
D2．已知
，则
（A）12 （B）8 （C）4 （D）2
D 3．下列函数中值域是R+的是
（A）
y=
（B）
（C）
（D）y=
D4．从集合{1，2，3，…，10}中任意选出三个不同的数，使这三个数成等比数列，这样的等比数列个数为
(A) 3 （B）4 (C) 6 （D）8
A5．数列1， 
，，，
，，，，，
……的前100项之和为
（A）10
（B）
（C）11
（D）
A 6．设
是由正数组成的等比数列，公比q=2,且
…
则
…
(A) 
（B）
(C) 
（D） 
C7．已知
，
，
与
的夹角为
，
，
，若
，则
的值为
（A）
（B）
（C）
（D）
B 8．如果
，则
一定在
(A)第一、三象限 (B)第二、四象限 (C)第三、四象限 (D)第一、二象限
C 9．在
中，
的面积为
，则
（A）
（B）
（C）
（D）
B10．函数
的图象的一条对称轴方程为
，则直线
的倾斜角是
(A) 45° （B）135° （C）60° （D）120°
二、填空题：本大题共6小题，每小题5分，共30分。不需要写出解答过程，请把答案直接填写在答题卷相应位置上。
11．夏季某高山上的温度从山脚起，每升高100米降低
，已知山顶处的温度是
，山脚温度是
，则这山的山顶相对于山脚处的高度是 1600 m ．
12．一条信息，若一人得知后，一小时内将信息传给两人，这两人又在一小时内各传给未知信息的另外两人.如此下去，要传遍55人的班级所需时间大约为__5_____小时.
13．已知
是偶函数，则函数
的图象的对称轴是 
14．已知
且
则Ａ∩Ｂ= 
15．定义运算
为：
，例如，
，则函数
的值域[－1，
]
16．给出下列四个函数：①
;②
;③
;④
,对于其定义域内的任意的
成立的函数为 ②③
三、解答题：本大题共5小题，共70分. 解答应写出文字说明，证明过程或演算步骤.
17．（本小题满分12分）有四个正数
，前三数成等比数列，其和为
；后三数成等差数列，其和为
．
（Ⅰ）求此四数；
（Ⅱ）分别求以
为前三项的等比数列的前
项和
与以
为前三项的等差数列的
前项和
；
（Ⅲ）比较与
的大小．
解：（Ⅰ）依题意有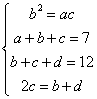
解得四数依次为
或
，因为四数均为正数。所以所求四数依次为
（Ⅱ）
，
（Ⅲ）当
时，
当
时，
18．（本小题满分16分）已知函数
.
（Ⅰ）求
的最小正周期及递减区间；
（Ⅱ）指出将函数
的图象经过怎样的变换而得到函数的图象；
（Ⅲ）若
, 求最大值、最小值．
解：（Ⅰ）
∴ 
递减区间
（Ⅱ）先把各点的横坐标缩小到原来的
（纵坐标不变），再向左平移
个单位，再把纵坐标扩大到原来的
倍（横坐标不变）而得到函数的图象
（Ⅲ）
当
即
时 
当
即
时 
19．（本小题满分14分）设
为公差大于0的等差数列，
为数列的前n项的和.
已知S4=24，
（Ⅰ）求数列的通项公式
；
（Ⅱ）若
的前n项和
解：（Ⅰ）
由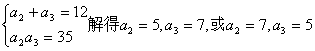
（Ⅱ）
20．（本小题满分14分）已知：定义在R上的函数f (x)为奇函数，且在
上是增函数.
（Ⅰ）求证：f (x)在
上也是增函数；
（Ⅱ）对任意
，求实数m的取值范围，使不等式
恒成立.
解：（Ⅰ）证明：设
，且
，
则
，且
.
∵
在
上是增函数，∴
.
又为奇函数，∴
,
∴
, 即在
上也是增函数.
（Ⅱ）∵函数在和上是增函数，且在R上是奇函数，
∴在
上是增函数.
于是
.
∵当
时，
的最大值为
，∴当
时，不等式恒成立.
21．（本小题满分14分）设函数
.
（Ⅰ）在区间
上画出函数
的图像；
（Ⅱ）设集合
. 试判断集合
和
之间的关系，并给出证明；
（Ⅲ）当
时，求证：在区间
上，
的图像位于函数图像的上方
解：（Ⅰ）
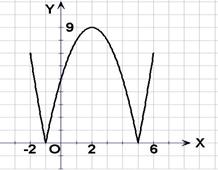
（Ⅱ）方程
的解分别是
和
，由于在
和
上单调递减，在
和
上单调递增，因此
.
由于
.
（Ⅲ）[解法一] 当
时，
.
，
. 又
，
①
当
，即
时，取
，
.
，
则
.
② 当
，即
时，取
， ＝
.
由 ①、②可知，当时，
，.
因此，在区间上，
的图像位于函数图像的上方.
[解法二] 当时，.
由
得
，
令 
，解得 
或
，
在区间上，当时，
的图像与函数的图像只交于一点
；
当时，
的图像与函数的图像没有交点.
如图可知，由于直线过点
，当时，直线是由直线绕点逆时针方向旋转得到. 因此，在区间上，的图像位于函数图像的上方.