高三年级调考数学试卷(文科)
注意事项:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集![]() ,集合
,集合![]() ,则
,则![]() (
)
(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 5人站成一排,甲、乙两人相邻的不同站法的种数为( )
A.24 B.36 C. 48 D. 60
3. 已知数列![]() 是等比数列,若
是等比数列,若![]() ,则数列
,则数列![]() 的前10项的积
的前10项的积![]() 等于(
)
等于(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 在![]() 中,
中,![]() (
(![]() 分别为角A,B,C的对边),则
分别为角A,B,C的对边),则![]() 的形状为(
)
的形状为(
)
A.正三角形 B.直角三角形 C.等腰直角三角形 D.等腰三角形或直角三角形
5. 已知平面上三点A、B、C满足![]() ,则
,则![]()
![]() 的值等于(
)
的值等于(
)
A. 25 B. 24 C.
![]() D.
D. ![]()
6.已知函数![]() ,
,![]() ,则“
,则“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
 C.充要条件
D.既不充分也不必要条件
C.充要条件
D.既不充分也不必要条件
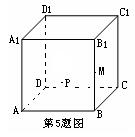
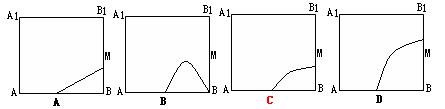
7.如图所示,在正方体![]() 的侧面
的侧面![]() 内有一动点P到平面
内有一动点P到平面![]() 的距离是到直线
的距离是到直线![]() 的距离的2倍,点M是棱
的距离的2倍,点M是棱![]() 的中点,则动点P所在曲线的大致形状为(
)
的中点,则动点P所在曲线的大致形状为(
)
8. 椭圆![]() 与直线
与直线![]() 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为![]() ,则
,则![]() 的值为(
)
的值为(
)
A. ![]() B.
B.![]() C.
C. ![]() D.
D.
![]()
9. 已知函数![]() 与
与![]() 的图象都过点
的图象都过点![]() ,且在点P处有公共切线,则函数
,且在点P处有公共切线,则函数![]() 的表达式为(
)
的表达式为(
)
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
10. 一次研究性课堂上,老师给出函数![]() ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数![]() 的值域为
的值域为![]() ;
;
乙:若![]() ,则一定有
,则一定有![]() ;
;
丙:若规定![]() ,则
,则![]() 对任意
对任意![]() 恒成立.
恒成立.
你认为上述三个命题中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
第Ⅱ卷
二.填空题:本大题共5小题,每小题5分,共25分,
11. ![]() 的展开式中
的展开式中![]() 的系数为______.(用数字作答)
的系数为______.(用数字作答)
12. 已知![]() 满足约束条件
满足约束条件 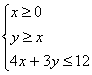 ,则
,则![]() 的取值范围是______.
的取值范围是______.
13. 已知双曲线![]() 的右焦点为F,右准线与一条渐近线交于点A,
的右焦点为F,右准线与一条渐近线交于点A,![]() 的面积为
的面积为![]() (O为原点),则双曲线的两条渐近线的夹角为______.
(O为原点),则双曲线的两条渐近线的夹角为______.
14. 若函数![]() 在
在![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是______.
的取值范围是______.
15. 直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数![]() 的图象恰好通过
的图象恰好通过![]() 个格点,则称函数
个格点,则称函数![]() 为
为![]() 阶格点函数.下列函数:①
阶格点函数.下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中是一阶格点函数的有______.(填上所有满足题意的序号)
,其中是一阶格点函数的有______.(填上所有满足题意的序号)
三.解答题:本大题共6小题,共75分.解答应写了文字说明,证明过程或演算步骤.
16. (本小题满分12分)
已知函数![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的最大值与最小值;
的最大值与最小值;
(Ⅱ)求函数![]() 的单调增区间.
的单调增区间.
17. (本小题满分12分)
已知函数![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值.
处取得极小值.
(Ⅰ)求![]() 的解析式并指出其单调区间;
的解析式并指出其单调区间;
(Ⅱ)讨论方程![]() 的实根的个数.
的实根的个数.
18. (本小题满分12分)
武昌区某中学举行春季运动会,高三某班杨萍同学参加女子乒乓球单打比赛.假定从开始的小组淘汰赛到最后决出冠亚军共经过5轮比赛.若杨萍同学在5轮比赛中顺利过关的概率依次为![]() .试问:
.试问:
(Ⅰ)杨萍同学获得该项冠军的可能性有多大?
(Ⅱ)杨萍同学在第二轮或第三轮被淘汰的概率是多少?
19. (本小题满分12分)
如图,在正四棱柱![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.
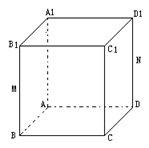 (Ⅰ)求异面直线
(Ⅰ)求异面直线![]() 与
与![]() 所成的角的余弦值;
所成的角的余弦值;
(Ⅱ)求证:平面![]() 平面
平面![]() .
.
20. (本小题满分12分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求证:![]() 为等差数列;
为等差数列;
(Ⅱ)求满足![]() 的自然数
的自然数![]() 的集合.
的集合.
21.(本小题满分14分)
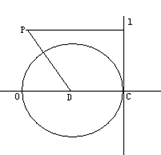 如图,已知直线
如图,已知直线![]() 与半径为1的⊙D相切于点C,动点P到直线
与半径为1的⊙D相切于点C,动点P到直线![]() 的距离为
的距离为![]() ,若
,若![]() .
.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若轨迹上的点P与同一平面上的点G、M分别满足![]() ,
,![]() ,求以P、G、D为顶点的三角形的面积.
,求以P、G、D为顶点的三角形的面积.