高三年级理科数学第一学期期中联考试卷
命题人:萧山中学 李金兴 审校:莫维平
一.选择题(每小题仅有一个答案正确,每小题5分,共50分)
1.复数![]() ,
,![]() (其中
(其中![]() ),那么
),那么![]() 是实数的充要条件是
是实数的充要条件是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.数列![]() 中,
中, ![]() ,
,![]() ,那么
,那么![]() 等于
等于
A.16 B.8 C.32 D.64
3.对于函数![]() ,下列叙述正确的是
,下列叙述正确的是
A.既有极大值又有最大值 B.有极大值但没有最大值
C.没有极大值但有最大值 D.既无极大值又无最大值
4.对于函数![]() (其中
(其中![]() 为某一实数),下列叙述正确的是
为某一实数),下列叙述正确的是
A.函数![]() 有最小值
有最小值![]() ;
B.函数
;
B.函数![]() 有最小值
有最小值![]() ;
;
C.函数![]() 有最大值
有最大值![]() D.函数
D.函数![]() 不一定有最值.
不一定有最值.
5.数列![]() 前
前![]() 项和
项和![]() ,其中
,其中![]() 成等比数列,那么
成等比数列,那么![]() 等于
等于
A.7 B.8 C.14 D.27
6.对于集合![]() ,若
,若![]() ,则一定有
,则一定有
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
7.设![]() ,
,![]() ,那么
,那么![]() 是
是![]() 的
的
A.充分不必要条件 B.必要不充分条件
C.充要条件 ![]() D.既不充分也不必要条件
D.既不充分也不必要条件
8.设![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,那么
,那么![]() 的最小值为
的最小值为
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
9.设![]() 是离散型随机变量,
是离散型随机变量, ![]() ,且
,且![]() ,又已知
,又已知![]() ,则
,则![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知函数![]() 的导函数为
的导函数为![]() ,且对于任意
,且对于任意![]() ,总有
,总有![]() 成立,那么
成立,那么![]() 与
与![]() 的大小关系为
的大小关系为
A.![]() >
>![]() B.
B.![]() =
=![]() C.
C.![]() <
<![]() D.不确定
D.不确定
二.填空(每小题4分,共16分)
11.已知集合![]() ,从
,从![]() 到
到![]() 的映射
的映射![]() 满足:
满足: ![]() 中的任何元素都有原象,且
中的任何元素都有原象,且![]() 中的元素之和为124,求
中的元素之和为124,求![]() .
.
12.设数列![]() 的通项
的通项![]() ,则
,则![]() .
.
13.定义在![]() 上的函数
上的函数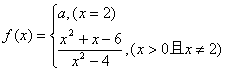 是
是![]() 上的连续函数,那么
上的连续函数,那么![]() .
.
14.关于![]() 的方程
的方程![]() 有实根,那么实数
有实根,那么实数![]() 的取值范围为__________________.
的取值范围为__________________.
三.解答题(6大题,每题14分,共84分)
15.已知![]() 为定义在
为定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() ;
;
(1)求![]() 时,
时, ![]() 的解析式;
的解析式;
(2)求![]() 的值域.
的值域.
16.无穷等比数列![]() 的各项都为正数,又
的各项都为正数,又![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)取出数列![]() 的前
的前![]()
![]() 项,设其中的奇数项之和为
项,设其中的奇数项之和为![]() ,偶数项之和为
,偶数项之和为![]() ;求出
;求出![]() 和
和![]() 的表达式(用
的表达式(用![]() 表示).
表示).
17.甲乙两袋中装有大小相同的红球和白球,甲袋中装有1个红球和2个白球,乙袋中装有2个红球和1个白球,现从甲乙两袋中各取2个球;设取出的4个球中红球的个数为![]() ,
,
(1)求![]() 的概率;
的概率;
(2)写出![]() 的分布列,并求出
的分布列,并求出![]() 的数学期望值.
的数学期望值.
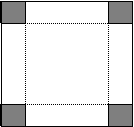
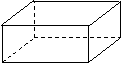
18.在边长为6的正方形纸板的四角切去相等的正方形,再沿虚线折起,做成一个无盖的方底箱子 (如图) ,
(1)当箱子容积最大时,切去的四个小正方形的边长恰为![]() ,求出
,求出![]() 的值;
的值;
(2)若将切下来的四个小正方形再按相同方法做成四个无盖的方底箱子,问:当五个箱子的体积总和最大时, 第一次切下来的四个小正方形的边长是否仍然为![]() ?说明理由.
?说明理由.
 | |||
 | |||
19.已知函数![]() ;
;
(1)求![]() ;
;
(2)设![]() ,求
,求![]() ;
;
(3)对于题(2)中所得的![]() ,设
,设![]() ,问:是否存在正整数
,问:是否存在正整数![]() ,使得对于任意
,使得对于任意![]() ,均有
,均有![]() 成立?若存在,求出
成立?若存在,求出![]() 的最小值,若不存在,说明理由.
的最小值,若不存在,说明理由.
20.设函数![]()
(1)若![]() 是
是![]() 上的单调函数,求
上的单调函数,求![]() 的取值范围并指出单调性;
的取值范围并指出单调性;
(2)若函数![]() 的定义域为
的定义域为![]() ,求出
,求出![]() 的取值范围;
的取值范围;
(3)若数列![]() 是递增数列,求出
是递增数列,求出![]() 的取值范围。
的取值范围。
参考答案
一.选择题(50分)
1.B 2.A 3.D 4.B 5.C 6.B 7.A 8.A 9.A 10.C
二.填空题(16分)
11.5 12.234 13.![]() 14.
14.![]()
三.解答题(84分)
15.(14分)
(1)![]() 时,
时, ![]() ;------------------------------------------6分
;------------------------------------------6分
(2)![]() 时,
时, ![]() ;
;
∴![]() 时,
时, ![]() ,
,![]() 时,
时, ![]() ,
,
由单调性易知:![]() 时,
时,![]() ; -----------------------------------------4分
; -----------------------------------------4分
而![]() 时,
时, ![]() ,又因为
,又因为![]() 是偶函数,
是偶函数,
由对称性易知![]() 的值域为
的值域为![]() .--------------------------------------------------4分
.--------------------------------------------------4分
16.(14分)
(1)由![]() 解得
解得![]() ,----------------------------------------3分
,----------------------------------------3分
因为数列各项为正,所以![]() ;
;![]() .--------------------------------3分
.--------------------------------3分
(2)![]() ;----------------------------------------------------4分
;----------------------------------------------------4分
![]() .-------------------------------------------------4分
.-------------------------------------------------4分
17.(14分)
(1) ![]() ;------------------------------------------6分
;------------------------------------------6分
(2) ![]() 的分布列为:
的分布列为:
|
| 1 | 2 | 3 |
|
|
|
|
|
-------------------6分-
所以, ![]() -------------------------------------------2分
-------------------------------------------2分
18.(14分)
(1)设切下来的小正方形边长为![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 1时
1时![]() ;
;
而![]() 时
时![]() ,
,![]() 时
时![]() ,所以
,所以![]() 时容积最大;即
时容积最大;即![]() .-----6分
.-----6分
(2)设第一次切下来的小正方形边长为![]() ,则五个箱子的容积之和为
,则五个箱子的容积之和为
![]() ----------------------------------------------------------4分
----------------------------------------------------------4分
因为![]() ,显然
,显然![]() 不是极值点,---------------------------------2分
不是极值点,---------------------------------2分
所以要使五个箱子的容积之和最大, 第一次切下来的小正方形边长不能为![]() .-2分
.-2分
19.(14分)
(1) ![]() ---------------------------------------------4分
---------------------------------------------4分
(2) 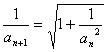 ,所以
,所以![]() ,而
,而![]() ,
,
所以![]() ,又
,又![]() 显然成立,所以
显然成立,所以![]() .---------------5分
.---------------5分
(3) ![]()
![]() ,-----------------------------2分
,-----------------------------2分
所以![]() ,故存在最小正整数
,故存在最小正整数![]() 使
使![]() 恒成立.--------3分
恒成立.--------3分
20.(14分)
(1) ![]() --------------------------------------------------1分
--------------------------------------------------1分
而![]() ------------------------------------------------------2分
------------------------------------------------------2分
所以, ![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 为增函数;
为增函数;
![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 为增减函数;--------------------------- 2分
为增减函数;--------------------------- 2分
(2) 即![]() 恒成立,若
恒成立,若![]() 显然成立;
显然成立;
若![]() ,则
,则![]() 恒成立,因为
恒成立,因为![]() ,所以
,所以![]() ;
;
若![]() ,则
,则![]() 恒成立,因为
恒成立,因为![]() ,所以
,所以![]() ;
;
综上所述, ![]() ---------------------------------------------------------4分
---------------------------------------------------------4分
(3) 法一:![]() 在
在![]() 上递增,所以
上递增,所以![]() 对于一切
对于一切![]() 恒成立,此时
恒成立,此时![]() ,所以
,所以![]() ;---------------------2分
;---------------------2分
又因为![]() ,所以
,所以![]() ---------------------------------------------------2分
---------------------------------------------------2分
综上所述, ![]() 时,数列递增.-----------------------------------------------1分
时,数列递增.-----------------------------------------------1分
法二: ![]()
![]() 恒成立-------------------------2分
恒成立-------------------------2分
而![]()
![]() (证略)
(证略)
所以![]() ----------------------------------------2分
----------------------------------------2分
综上所述, ![]() 时,数列递增.-----------------------------------------------1分
时,数列递增.-----------------------------------------------1分