高三年级数学模拟试题(文科)
浠水一中 巩震 程强
第Ⅰ卷(选择题 共50分)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中只有一个选项是符合题目要求的.把选项填在答卷的表格中).
1、定义集合运算:A⊙B={![]() ,x∈A,y∈B},设集合A={
,x∈A,y∈B},设集合A={![]() ,0,1},B=
,0,1},B=
{![]() },则集合A⊙B的所有元素之和为
},则集合A⊙B的所有元素之和为
A、1
B、0
C、![]() D、
D、![]()
2、x>0是![]() -1>0成立的
-1>0成立的
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
3、若数列{an}满足a1=5,an+1=![]() +
+![]() (n∈N+),则其{an}的前10项和为
(n∈N+),则其{an}的前10项和为
A、50 B、100 C、150 D、200
4、设f(x)=tan3x+![]() tan3x
tan3x![]() ,则f(x)为
,则f(x)为
A、周期函数,最小正周期为![]() B、周期函数,最小正周期为
B、周期函数,最小正周期为![]()
C、周期函数,最小正周期为![]() D、非周期函数
D、非周期函数
5、动点P(m,n)到直线![]() 的距离为λ
的距离为λ![]() ,点P的轨迹为双曲线(且原点O为准线l对应的焦点),则λ的取值为
,点P的轨迹为双曲线(且原点O为准线l对应的焦点),则λ的取值为
A、λ∈R B、λ=1 C、λ>1 D、0<λ<1
6、已知函数f(x)= 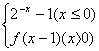 ,若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是
,若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、四面体的一个顶点为A,从其它顶点与棱的中点中任取3个点,使它们和点A在同一平面上,不同的取法有
A、30种 B、33种 C、36种 D、39种
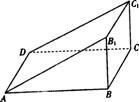 8、如图,直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,
8、如图,直三棱柱ABB1-DCC1中,∠ABB1=90°,AB=4,BC=2,
CC1=1,DC上有一动点P,则ΔAPC1周长的最小值为
A、5+![]() B、5-
B、5-![]() C、4+
C、4+![]() D、4-
D、4-![]()
9、已知函数f(x)=![]() ,设
,设![]() =
=![]() ,若
,若![]() ≤x1<0<x2<x3,则
≤x1<0<x2<x3,则
A、a2<a3<a4 B、a1<a2<a3 C、a1<a3<a2 D、a3<a2<a1
10、函数y=![]() 的图象为双曲线,则该双曲线的焦距为
的图象为双曲线,则该双曲线的焦距为
A、4![]() B、2
B、2![]() C、4 D、8
C、4 D、8
第Ⅱ卷(非选择题 共100分)
二、填空题:(本大题共5小题,每小题5分,共25分.)
11、已知(x![]()
![]() )n的展开式中第二项与第三项的系数之和等于27,则n等于 ,系数最大的项是第
项。
)n的展开式中第二项与第三项的系数之和等于27,则n等于 ,系数最大的项是第
项。
12、若不等式1-loga![]() <0有解,则实数a的范围是
。
<0有解,则实数a的范围是
。
13、在ΔABC中,cos2B=![]() ,则角B的大小为
。
,则角B的大小为
。
14、三个好朋友同时考进同一所高中,该校高一有10个班,则至少有2人分在同一班的概率为 。
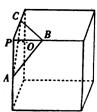 15、若RtΔABC中两直角边为a、b,斜边c上的高为h,则
15、若RtΔABC中两直角边为a、b,斜边c上的高为h,则![]() ,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=
,如图,在正方体的一角上截取三棱锥P-ABC,PO为棱锥的高,记M=![]() ,N=
,N=![]() ,那么M、N的大小关系是
。
,那么M、N的大小关系是
。
三、解答题:(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤)
16、(本题满分12分)
已知函数f(x)= ![]() +2sin2x
+2sin2x
(1)求函数f(x)的最大值及此时x的值;
(2)求函数f(x)的单调递减区间。
17、(本题满分12分)
四个纪念币A、B、C、D,投掷时正面向上的概率如下表所示(0<a<1)
| 纪念币 | A | B | C | D |
| 概率 | 1/2 | 1/2 | a | a |
这四个纪念币同时投掷一次,设ξ表示出正面向上的个数。
(1)求概率p(ξ)
(2)求在概率p(ξ),p(ξ=2)为最大时,a的取值范围。
18、(本题满分12分)
如图①在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G分别是线段PC、PD,BC的中点,现将ΔPDC折起,使平面PDC⊥平面ABCD(如图②)
(1)求证AP∥平面EFG;
(2)求二面角G-EF-D的大小;
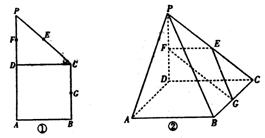 (3)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明。
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,试给出证明。
19、(本题满分12分)
在平面直角坐标系中,已知A1(-3,0),A2(3,0),P(x,y),M(![]() ,0),若实数λ使向量
,0),若实数λ使向量![]() ,λ
,λ![]() ,
,![]() 满足λ2·(
满足λ2·(![]() )2=
)2=![]() ·
·![]() 。
。
(1)求点P的轨迹方程,并判断P点的轨迹是怎样的曲线;
(2)当λ=![]() 时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使ΔA1BC为正三角形(请说明理由)。
时,过点A1且斜率为1的直线与此时(1)中的曲线相交的另一点为B,能否在直线x=-9上找一点C,使ΔA1BC为正三角形(请说明理由)。
20、(本题满分13分)
已知a为实数,函数f(x)=(x2+![]() )(x+a)
)(x+a)
(1)若函数f(x)的图象上有与x轴平行的切线,求a的取值范围;
(2)若f'(-1)=0,(Ⅰ)求函数f(x)的单调区间;(Ⅱ)若对任意的x1,x2∈[-1,0],不等式![]() f(x1)-f(x2)
f(x1)-f(x2)![]() ≤m恒成立,试求m的最小值。
≤m恒成立,试求m的最小值。
21、(本题满分14分)
已知函数![]() 与函数
与函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(1)试用含![]() 的代数式表示函数
的代数式表示函数![]() 的解析式,并指出它的定义域;
的解析式,并指出它的定义域;
(2)数列![]() 中,
中,![]() ,当
,当![]() 时,
时,![]() .数列
.数列![]() 中,
中,![]() ,
,![]() .点
.点![]() 在函数
在函数![]() 的图像上,求
的图像上,求![]() 的值;
的值;
(3)在(2)的条件下,过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,则
,则![]() 在y轴上的截距为
在y轴上的截距为![]()
![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
高三年级数学模拟试题(文科)
参考答案及评分标准
一、选择题
1、当χ=-1,1,y∈B,所得元素之和为0,放A⊙B所有元素之和为0 选B
2、![]() -1>0
-1>0![]()
![]() <0
<0![]() 0<x<1 故选B
0<x<1 故选B
3、由an+1=![]() +
+![]() 得a
得a![]() -2anan+1+a
-2anan+1+a![]() =0 ∴an+1= an
=0 ∴an+1= an
即{an}为常数列 S10=10a1=50 ∴选A
4、作出f(x)的图象,当0≤x<![]() 时,f(x)=2tan3x,当
时,f(x)=2tan3x,当![]() <x≤
<x≤![]() 时,f(x)=0,由图象知f(x)为周期函数,最小正周期为
时,f(x)=0,由图象知f(x)为周期函数,最小正周期为![]() ,故选A。
,故选A。
5、D 由双曲线定义及点P(m,n)到原点的距离为![]() 可得:
可得:
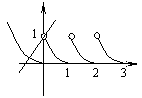 e=
e=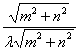 =
=![]() >1, ∴0<λ<1,故选D。(也可直接用解析法推导)
>1, ∴0<λ<1,故选D。(也可直接用解析法推导)
6、作出函数f(x)的图象,要使斜率为1的直线与y=f(x),有两个不同的交点,必须a<1,故选C。
7、四面体有四个顶点,6条棱有6个中点,每个面上6个点共面。点A所在的每个面中含A的4点组合有C![]() 个,点A在三个面内,共有3C
个,点A在三个面内,共有3C![]() ;点A在6条棱的3条棱上,每条棱上有3个点,这3个点与这条棱对棱的中点共面,∴符合条件的个数有3C
;点A在6条棱的3条棱上,每条棱上有3个点,这3个点与这条棱对棱的中点共面,∴符合条件的个数有3C![]() +3=33个,选B。
+3=33个,选B。
8、在直三棱柱ABB1=DCC1中,AC1=![]()
将△DCC1展开与矩形ABCD在同一平面内,AP+PC1最小,此时
AP+PC1为![]() ,∴周长最小值为5+
,∴周长最小值为5+![]() ,故选A。
,故选A。
9、画出函数f(x)=-![]() 的图象,则an=
的图象,则an=![]() 表示曲线上动点(xn、f(xn))与定点(0,2)所在直线的斜率,显然a2<a3<0<a1 故选A
表示曲线上动点(xn、f(xn))与定点(0,2)所在直线的斜率,显然a2<a3<0<a1 故选A
10、D,易知此双曲线为等轴双曲线,其一条对称轴y=x和它的交点为(2,2)、(-2,-2),于是实半轴长为2![]() ,由对称性知虚半轴长也为2
,由对称性知虚半轴长也为2![]() ,从而焦距为8。
,从而焦距为8。
二、填空题
11、Tr+1=![]() (x
(x![]() )n-r(-
)n-r(-![]() )r,由题意知:-
)r,由题意知:-![]() +
+![]() =27
=27![]() n=9
n=9
∴展开式共有10项,二项式系数最大的项为第五项或第六项,故项的系数最大的项为第五项。
12、当a>1时,不等式化为10-ax>a,要使不等式有解,必须10-a>0
∴1<a<10
当0<a<1时,不等式化为0<10-ax<a![]() 10-a<ax<10不等式恒有解
10-a<ax<10不等式恒有解
故满足条件a的范围是(0,1)∪(1,10)
13、∵0<2B<2π ∴2B=![]() π或
π或![]() π 故B=
π 故B=![]() π或
π或![]() π
π
14、P=1-![]() =
=![]()
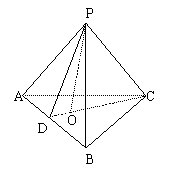 15、如图,连CO交AB于D点,∵PC⊥面APB,PO⊥底ABC
15、如图,连CO交AB于D点,∵PC⊥面APB,PO⊥底ABC
∴AB⊥面PDC,即AB⊥PD,∵ΔCPD为RtΔ
故由已知得: ![]() =
=![]() +
+![]()
![]() =
=![]() +
+![]() ,故M=N
,故M=N
三、解答题
16、解:(1)∵cos3x=4cos3x-3cosx,则![]() =4cos2x-3=2cos2x-1
=4cos2x-3=2cos2x-1
∴f(x)=2cos2x-1+2sin2x
=2![]() sin(2x+
sin(2x+![]() )-1
……………………4分
)-1
……………………4分
在2x+![]() =2kπ+
=2kπ+![]() 时,f(x)取得最大值2
时,f(x)取得最大值2![]() -1
-1
即在x=kπ+![]() (k∈Z)时,f(x)取得最大值2
(k∈Z)时,f(x)取得最大值2![]() -1 ……………………6分
-1 ……………………6分
(2)∵f(x)=2![]() sin(2x+
sin(2x+![]() )-1
)-1
要使f(x)递减,x满足2kπ+![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]()
即kπ+![]() ≤x≤kπ+
≤x≤kπ+![]() (k∈Z)
(k∈Z)
又∵cosx≠0,即x≠kπ+![]() (k∈Z)
……………………10分
(k∈Z)
……………………10分
|
|
17、解:(1)p(ξ个正面向上,4-ξ个背面向上的概率,其中ξ可能取值为0,1,2,3,4。
∴p(ξ=0)=
![]() (1-
(1-![]() )2
)2![]() (1-a)2=
(1-a)2=![]() (1-a)2
(1-a)2
p(ξ=1)= ![]()
![]() (1-
(1-![]() )
)![]() (1-a)2+
(1-a)2+![]() (1-
(1-![]() )2·
)2·![]() a(1-a)=
a(1-a)= ![]() (1-a)
(1-a)
p(ξ=2)= ![]() (
(![]() )2
)2![]() (1-a)2+
(1-a)2+![]()
![]() (1-
(1-![]() )
)![]() a(1-a)+
a(1-a)+ ![]() (1-
(1-![]() )2·
)2·![]() a2=
a2=![]() (1+2a-2 a2)
(1+2a-2 a2)
p(ξ=3)= ![]() (
(![]() )2
)2![]() a(1-a)+
a(1-a)+ ![]()
![]() (1-
(1-![]() )
)![]() a2=
a2=![]()
p(ξ=4)= ![]() (
(![]() )2
)2![]() a2=
a2=![]() a2
……………………6分
a2
……………………6分
(2)∵0<a<1,∴p(ξ=1) <p(ξ=1),p(ξ=4) <p(ξ=3)
则p(ξ=2)-
p(ξ=1)= ![]() (1+2a-2 a2)-
(1+2a-2 a2)- ![]() =-
=-![]() ≥0
≥0
由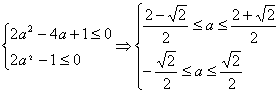
![]() ,即a∈[
,即a∈[![]() ] …………………………12分
] …………………………12分
18、解:(1)∵EF∥CD∥AB,EG∥PB,根据面面平行的判定定理
∴平面EFG∥平面PAB,又PA![]() 面PAB,∴AP∥平面EFG …………4分
面PAB,∴AP∥平面EFG …………4分
(2)∵平面PDC⊥平面ABCD,AD⊥DC
∴AD⊥平面PCD,而BC∥AD,∴BC⊥面EFD
过C作CR⊥EF交EF延长线于R点连GR,根据三垂线定理知
∠GRC即为二面角的平面角,∵GC=CR,∴∠GRC=45°,
故二面角G-EF-D的大小为45°。 …………………………8分
(3)Q点为PB的中点,取PC中点M,则QM∥BC,∴QM⊥PC
在等腰Rt△PDC中,DM⊥PC,∴PC⊥面ADMQ ………………12分
19、解:(1)由已知可得,![]() =(x+3,y),
=(x+3,y),![]() =(x-3,y),
=(x-3,y),![]() =(
=(![]() ,0),
,0),
∵![]() 2(
2(![]() )2=
)2=![]() ·
·![]() ,∴
,∴![]() 2(x2-9)=x2-9+y2,
2(x2-9)=x2-9+y2,
即P点的轨迹方程(1-![]() 2)x2+y2=9(1-
2)x2+y2=9(1-![]() 2)…………………………3分
2)…………………………3分
当1-![]() 2>0,且
2>0,且![]() ≠0,即
≠0,即![]() ∈(-1,0)时,有
∈(-1,0)时,有![]() +
+![]() =1,
=1,
∵1-![]() 2>0,∴
2>0,∴![]() >0,∴x2≤9。
>0,∴x2≤9。
∴P点的轨迹是点A1,(-3,0)与点A2(3,0)
当![]() =0时,方程为x2+y2=9,P的轨迹是点A1(-3,0)与点A2(3,0)
=0时,方程为x2+y2=9,P的轨迹是点A1(-3,0)与点A2(3,0)
当1-![]() 2<0,即入∈(-∞,-1)∪(1,+∞)时,方程为
2<0,即入∈(-∞,-1)∪(1,+∞)时,方程为![]() -
-![]() =1,P点的轨迹是双曲线。
……………………………………………………6分
=1,P点的轨迹是双曲线。
……………………………………………………6分
当1-![]() 2=0,即
2=0,即![]() =±1时,方程为y=0,P点的轨迹是射线。
=±1时,方程为y=0,P点的轨迹是射线。
(2)过点A1且斜率为1的直线方程为y=x+3,
当![]() =
=![]() 时,曲线方程为
时,曲线方程为![]() +
+![]() =1,
=1,
由(1)知,其轨迹为点A1(-3,0)与A2(3,0)
因直线过A1(-3,0),但不过A2(3,0)。
所以,点B不存在。
所以,在直线x=-9上找不到点C满足条件。……………………………………12分
20、解:(1)∵f(x)=x3+ax2+![]() x+
x+![]() a,∴f1(x)=3x2+2ax+
a,∴f1(x)=3x2+2ax+![]() .
.
∵函数f(x)的图象上有与x轴平行的切线,∴f1(x)=0有实数解,∴△=4a2-4×3×3/2≥0, ∴a2≥9/2,因此,所求实数a的取值范围是(-∞,-![]() )∪(
)∪(![]() ,+∞).…………4分
,+∞).…………4分
(2)(I)∵f'(-1)=0,∴3-2a+3/2=0,即a=9/4,f'(x)=3x2+2ax+3/2=3(x+1/2)(x+1).由f'(x) >0,得x<-1或x>-1/2,由f'(x) <0,得-1<x<-1/2.
因此,函数f(x)的单调增区间为(-∞,-1],[-1/2,+∞);
单调减区间为[-1,-1/2] ………………………………8分
(ii)由(I)的结论可知,f(x)在[-1,-1/2]上的最大值为f(-1)=25/8,最小值为f(-1/2)=49/16,f(x)在[-1/2,0]上的最大值为f(0)=27/8,最小值为f(-1/2)=49/16,∴f(x)在[-1,0]上的最大值为f(0)=27/8,最小值为f(-1/2)=49/16。因此,任意的x1,x2∈[-1,0],恒有f(x1)-f(x2)
≤![]() .故mmin=
.故mmin=![]() ………………………………13分
………………………………13分
21、解:(1)由题可知:![]() 与函数
与函数![]() 互为反函数,所以,
互为反函数,所以,
![]() ,
,![]() …………………………2分
…………………………2分
(2)因为点![]() 在函数
在函数![]() 的图像上,所以,
的图像上,所以,
![]()
![]() (*)
(*)
在上式中令![]() 可得:
可得:![]() ,又因为:
,又因为:![]() ,
,![]() ,代入可解得:
,代入可解得:![]() .所以,
.所以,![]() ,(*)式可化为:
,(*)式可化为:![]()
![]() ①……6分
①……6分
(3)直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,
在其中令![]() ,得
,得![]() ,又因为
,又因为![]() 在y轴上的截距为
在y轴上的截距为![]() ,所以,
,所以,
![]() =
=![]() ,结合①式可得:
,结合①式可得:![]() ②
②
由①可知:当自然数![]() 时,
时,![]() ,
,![]() ,两式作差得:
,两式作差得:![]() .
.
结合②式得:![]()
![]() ③
③
在③中,令![]() ,结合
,结合![]() ,可解得:
,可解得:![]() ,
,
又因为:当![]() 时,
时,![]() ,所以,舍去
,所以,舍去![]() ,得
,得![]() .
.
同上,在③中,依次令![]() ,可解得:
,可解得:![]() ,
,![]() .
.
猜想:![]()
![]() .下用数学归纳法证明. …………………………10分
.下用数学归纳法证明. …………………………10分
(1)![]() 时,由已知条件及上述求解过程知显然成立.
时,由已知条件及上述求解过程知显然成立.
(2)假设![]() 时命题成立,即
时命题成立,即![]()
![]() ,则由③式可得:
,则由③式可得:
![]()
把![]() 代入上式并解方程得:
代入上式并解方程得:![]()
由于![]() ,所以,
,所以,![]() ,所以,
,所以,![]()
符合题意,应舍去,故只有![]() .
.
所以,![]() 时命题也成立.
时命题也成立.
综上可知:数列![]() 的通项公式为
的通项公式为![]()
![]() …………………………14分
…………………………14分