高三阶段测试数学试题(理科 ）
班级_________姓名__________学号___________成绩_______
一、选择题：本大题共12小题，每小题5分，满分60分
1．下列命题不正确的是
（ ）
A．如果 f (x) = ，则 f (x) = 0
B．如果 f (x) = 2 x－1，则 f (x) = 0
C．如果 f (n)
= ，则 f (n) 不存在
D．如果 f (x)
= ，则 f (x) = 0
2．
是 f (x)在点x0连续的
( )
A．充分不必要条件 B．充要条件
C．既不充分也不必要条件 D．必要不充分条件
3．与直线
平行的曲线
的切线方程是
（ ）
A．
B．
或
C． D．或
4．采用系统抽样的方法，从个体数为1003的总体中抽取一个容量为50的样本，在整个抽样过程中每个个体被抽到的概率是
（ ）
A．
B．
C．
D．
5．点P在曲线
上移动，在点P处的切线的倾斜角为α，则α的取值范围是（ ）
A．
B．
C．
D．
6．某社区有500个家庭，其中高收入家庭125户，中等收入家庭280户，低收入家庭95户，
为了调查社会购买力的某项指标，要从中抽取一个容量为100户的样本，记作①。某学
校高一年级有12名女排运动员，要从中选出3人调查学习负担情况，记作②。那么完成
上述两项调查应采取的抽样方法是 （ ）
A. ①用随机抽样法，②用系统抽样法 B. ①用分层抽样法，②用随机抽样法
C. ①用系统抽样法，②用分层抽样法 D. ①用分层抽样法，②用系统抽样法
7．函数y=sin3(3x+
)的导数为
（ ）
A．3sin2(3x+)cos(3x+)
B．9sin2(3x+)cos(3x+)
C．9sin2(3x+)
D．－9sin2(3x+)cos(3x+)
8．函数
的图象关于原点中心对称，则f (x) （ ）
A．在[
]上为增函数
B．在[]上非单调函数
C．在[
上为增函数，（
为减函数
D．在（
）为增函数，在[上也为增函数
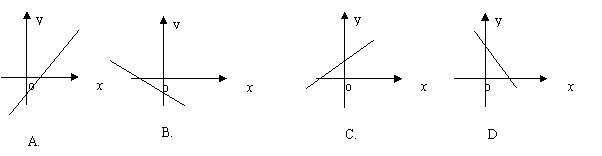9．若函数f(x)=x2+bx+c的图象的顶点在第四象限，则函数f /(x)的图象是 （ ）
10．设
为可导函数，且满足
，则过曲线
上点
（1, f（1））处的切线斜率为 ( )
A．2 B．－1 C．1 D．－2
11．用数学归纳法证明等式：
=
从“
到
”左端需增乘的代数式为
（ ）
A．
B．
C．
D．
12．
成立的条件是
（ ）
A．
B．
C．
D．
二、填空题：本大题共4小题，每小题5分，共20分． 把答案填在题中横线上．
13．复数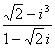
=
_________
14．函数f(x)=sin2x－x在［－
,］上的最大值为_______ 最小值为________
15．
，则a＋b = _____
16．调查某单位职工健康状况，其青年人数为300，中年人数为150，老年人数为100，现考虑采用分层抽样，抽取容量为22的样本，则青年、中年、老年各层中应抽取的个体数分别为___________________________
三、解答题：本大题共4小题，共70分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分16分）
已知函数f (x)=kx3－3(k+1)x2－k2+1(k>0)．若f (x)的单调递减区间是（0，4），
求k的值.
18. （本小题满分18分）
已知a为实数，
（Ⅰ）求导数
；
（Ⅱ）若
，求在[-2，2] 上的最大值和最小值；
（Ⅲ）若在（—∞，—2）和[2，+∞)上都是递增的，求a的取值范围.
19. （本小题满分18分）
某工厂生产某种产品，已知该产品的月生产量
（吨）与每吨产品的价格
（元/吨）之间的关系式为：
,且生产x吨的成本为
（元）.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）
20．（本小题满分18分）
已知定义在实数集R上的函数
是实数.
（Ⅰ）若函数在区间
上都是增函数，在区间（－1，3）上是减函数，并且
求函数的表达式；
（Ⅱ）若
，求证：函数是单调函数．
大峪中学高三阶段测试数学试题
参考答案
一、选择题：
1．D 2.D 3.D 4.C 5.B 6.B 7.B 8.D 9.A 10.B 11.B 12.C
二、填空题：
13．i 14. 
, 
15.3
16.12,6,4
三、解答题：
17. （本小题满分12分）
已知函数f(x)=kx3－3(k+1)x2－k2+1(k>0).若f(x)的单调递减区间是（0，4），
求k的值.
解： f ′(x)=
3kx2－6(k+1)x 由f ′(x)<0
得 0<x<
∵f (x)的递减区间是（0，4） ∴=4, ∴k=1
18．（本小题满分12分）
已知a为实数，
（Ⅰ）求导数；
（Ⅱ）若，求在[-2，2] 上的最大值和最小值；
（Ⅲ）若在（—∞，—2）和[2，+∞]上都是递增的，求a的取值范围.
解: (Ⅰ)由原式得
∴
(Ⅱ)由 得
,此时有
.
由得
或x=-1 , 又
所以f(x)在[--2,2]上的最大值为
最小值为
(Ⅲ)解法一: 
的图象为开口向上且过点(0,--4)的抛物线,由条件得
即
∴--2≤a≤2.
所以a的取值范围为[--2,2].
解法二:令
即
由求根公式得: 
所以在
和
上非负.
由题意可知,当x≤-2或x≥2时, ≥0,
从而x1≥-2, x2≤2,
即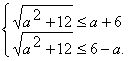
解不等式组得: --2≤a≤2.
∴a的取值范围是[--2,2].
19. （本小题满分12分）
某工厂生产某种产品，已知该产品的月生产量（吨）与每吨产品的价格（元/吨）之间的关系式为：,且生产x吨的成本为（元）.问该厂每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）
解：每月生产x吨时的利润为
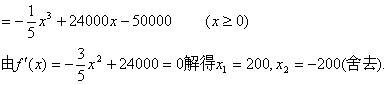
，故它就是最大值点，且最大值为：
答：每月生产200吨产品时利润达到最大，最大利润为315万元.
20．（本小题满分12分）
已知定义在实数集R上的函数是实数.
（Ⅰ）若函数在区间上都是增函数，在区间（－1，3）上是减函数，并且求函数的表达式；
（Ⅱ）若，求证：函数是单调函数．
解（1）
由
又由于在区间上是增函数，在区间（－1，3）上是减函数，
所以－1和3必是的两个根.
从而
又根据
（2）
因为为二次三项式，并且
，
所以，当
恒成立，此时函数是单调递增函数；
当
恒成立，此时函数是单调递减函数.
因此，对任意给定的实数a，函数总是单调函数.