高三届数学第二次诊断考试
(理科)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
1.答第Ⅰ卷前,请务必将自己的姓名、准考证号、考试科目,用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在考题卷上。
3.考试结束后,将本试卷和答题卡一并交回。
4.参考公式:
如果事件A、B互斥,那么![]() 。
。
如果事件A、B相互独立,那么![]()
如果事件A在一次试验中发生的概率是p,那么n次独立重复试验中恰好发生k次的概率为![]()
一、选择题:本大题共有12个小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合要求的。
1.已知集合![]() ,若
,若![]() ,则
,则
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2. 抛物线![]() 的焦点坐标是
的焦点坐标是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.随机变量![]() ,记
,记![]() ,则下列式子中错误的是
,则下列式子中错误的是
(A)![]() (B)
(B) ![]()
(C)![]() (D)
(D)![]()
4. “a,b为异面直线”是指:
①![]() ,且a与b不平行; ②a
,且a与b不平行; ②a![]() 平面
平面![]() ,b
,b![]() 平面
平面![]() ,且
,且![]() ;
;
③a![]() 平面
平面![]() ,b
,b![]() 平面
平面![]() ,且
,且![]() ; ④a
; ④a![]() 平面
平面![]() ,b
,b![]() 平面
平面![]() ;
;
⑤不存在平面![]() ,能使a
,能使a![]()
![]() 且b
且b![]()
![]() 成立。
成立。
上述结论中,正确的是
(A)①④⑤正确 (B)①⑤正确 (C)②④正确 (D)①③④正确
5.若不等式![]() 对于一切
对于一切![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围
的取值范围
(A)![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
6.复数![]() 是纯虚数,则
是纯虚数,则![]() 的值是
的值是
(A)![]() (B) 1 (C)
(B) 1 (C) ![]() (D)
(D)![]()
7.直线![]() 的倾斜角是
的倾斜角是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.按ABO血型系统学说,每个人的血型为A,B,O,AB型四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女的血型一定不是O型,若某人的血型是O型,则其父母血型的所有可能情况有
(A)12 (B)10 (C)9 (D)6
9.若二项式![]()
![]() 展开式中含有常数项,则
展开式中含有常数项,则![]() 的最小取值是
的最小取值是
(A)5 (B)6 (C)7 (D)8
10.已知一个全面积为24的正方体,内有一个与每条棱都相切的球,此球的体积为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.数列![]() 是一个单调递增数列,则实数
是一个单调递增数列,则实数![]() 的取值范围是
的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12.已知![]() 为
为![]() 与
与![]() 中较小者,其中
中较小者,其中![]() ,若
,若![]() 的值域为
的值域为![]() ,则
,则![]() 的值是
的值是
(A)0 (B)![]() (C)
(C)![]() (D)
(D)![]()
高三届数学第二次诊断考试
第Ⅱ卷(非选择题,共90分)
注意事项
1.第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中。
2.答卷前将密封线内项目填写清楚。
|
| 第Ⅰ卷 | 第Ⅱ卷 | 总分 | 总分人 | ||||||
| 题号 | 一 | 二 | 三 | |||||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||||
| 得分 |
|
|
|
|
|
|
|
|
|
|
| 得分 | 评卷人 |
|
|
|
二、填空题(本大题共4小题,每小题4分,共16分,将正确答案填在试题的横线上)
|
| 2 | 1 | 0 |
|
|
|
|
|
13.随机变量![]() 服从于如右表所示的分布列,其中
服从于如右表所示的分布列,其中![]() ,则
,则![]() 的最大值为_______.
的最大值为_______.
14.在![]() 中,角
中,角![]() 对应的边长为
对应的边长为![]() ,若
,若![]() ,则
,则![]() 的形状是_____________三角形.
的形状是_____________三角形.
15.若函数![]() 是定义在实数集上的奇函数,且
是定义在实数集上的奇函数,且![]() ,给出下列结论:
,给出下列结论:
①![]() ;②
;②![]() 以4为周期;③
以4为周期;③![]() 的图象关于
的图象关于![]() 轴对称;④
轴对称;④![]() .
.
这些结论中正确的有____________(必须填写序号).
16.过圆锥曲线(椭圆、双曲线、抛物线之一)某个焦点有一条弦AB,以AB为直径的圆与此焦点相应的准线没有交点,则该圆锥曲线的离心率取值范围是____________.
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
| 得分 | 评卷人 |
|
|
|
17.(本题满分12分)
已知向量![]() ,设
,设![]()
① 若![]() ,求
,求![]() 的值域.
的值域.
② 若![]() 的图象可以按向量
的图象可以按向量![]() 平移后得到
平移后得到![]() 的图象,指出向量
的图象,指出向量![]() 的一个值.
的一个值.
| 得分 | 评卷人 |
|
|
|
18.(本题满分12分)
已知![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() ,且
,且![]() ,其中
,其中![]() .
.
① 求数列![]() 的通项公式
的通项公式![]() ;
;
② 计算![]() 的值.
的值.
| 得分 | 评卷人 |
|
|
|
19.(本题满分12分)
如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,D为
,D为![]() 的中点.
的中点.
①
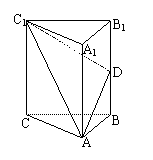 证明:平面
证明:平面![]() 平面
平面![]() ;
;
②
求点![]() 到平面的距离
到平面的距离![]() ;
;
③
求平面![]() 与平面
与平面![]() 所成的二面角大小.
所成的二面角大小.
| 得分 | 评卷人 |
|
|
|
20.(本题满分12分)
 今有一张长2米宽1米的矩形铁板,如图,在四个角上分别截去一个边长为
今有一张长2米宽1米的矩形铁板,如图,在四个角上分别截去一个边长为![]() 米的正方形后,沿虚线折起可做成一个长方体水箱(接口连接问题不考虑)。
米的正方形后,沿虚线折起可做成一个长方体水箱(接口连接问题不考虑)。
①
如果要使得水箱容积最大,则![]() 应取多少米?
应取多少米?
②
若要使水箱容积不大于4![]() 立方米的同时,又使得底面积最大以增加稳定性,
立方米的同时,又使得底面积最大以增加稳定性,![]() 应取什么值?
应取什么值?
| 得分 | 评卷人 |
|
|
|
21.(本题满分12分)
已知直线![]() 过椭圆E:
过椭圆E:![]() 的右焦点
的右焦点![]() ,且与E相交于
,且与E相交于![]() 两点.
两点.
① 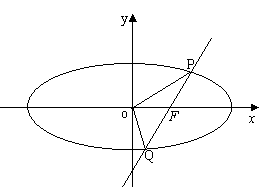 设
设![]() (
(![]() 为原点),求点
为原点),求点![]() 的轨迹方程;
的轨迹方程;
② 若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() 的值.
的值.
| 得分 | 评卷人 |
|
|
|
22.(本题满分14分)
已知关于![]() 的方程
的方程![]() 的两个根为
的两个根为![]() ,设函数
,设函数![]() .
.
① 判断![]() 在
在![]() 上的单调性;
上的单调性;
② 若![]() ,证明
,证明![]() .
.
高三届数学第二次诊断考试参考答案与评分标准
一、 选择题:
BCDBA CBCCD AD
二、 填空题
13.1; 14.等腰; 15. ①②④; 16.![]()
三、 解答题
17. 解:①![]() .........................2’
.........................2’
![]()
![]() .............................5’
.............................5’
![]()
![]()
![]() ..................8’
..................8’
②![]() ....................10’
....................10’
可见![]() 的图象向左平移
的图象向左平移![]() 个单位可得
个单位可得![]() 的图象,即
的图象,即![]() 的一个值是
的一个值是![]() .................................................................12’
.................................................................12’
18. 解:①![]()
![]()
![]()
![]()
![]()
![]() .............................................2’
.............................................2’
又![]() 也满足上式,
也满足上式,![]()
![]()
![]()
![]() (
(![]() )
)
![]() 数列
数列![]() 是公比为2,首项为
是公比为2,首项为![]() 的等比数列..................4’
的等比数列..................4’
![]()
![]() .................................6’
.................................6’
②![]()
![]()
![]()
![]() ...........................9’
...........................9’
于是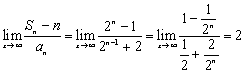 ........................12’
........................12’
19. 解:由勾股定理知,![]() ,则如图所示建立直角坐标系,坐标分别为:
,则如图所示建立直角坐标系,坐标分别为:

![]()
![]()
(1)![]()
![]() 分别是
分别是![]() 之中点。
之中点。
![]()
故![]()
![]()
![]() ,
,![]()
![]() 面
面![]() ,
,
![]() 平面
平面![]() 面
面![]() 。………………4分
。………………4分
(2)设平面![]() 的法向量
的法向量![]() ,且
,且![]()
令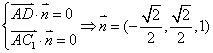 ,又
,又![]()
![]()
则,设点![]() 到平面的距离
到平面的距离![]() 为d
为d
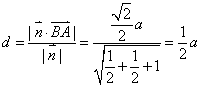 ………………………………8分
………………………………8分
(3)显然平面ABC的法向量为![]() ,平面
,平面![]() 的法向量
的法向量![]()
![]()
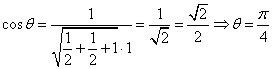 ,故两平面的夹角为
,故两平面的夹角为![]() …………12分
…………12分
20. ①易见该立方体底面长为![]() ,宽
,宽![]() ,高
,高![]()
所以,该立方体体积为![]()
![]() .............2’
.............2’
其中正数![]() 满足
满足![]() .................................3’
.................................3’
![]() ,..............................................5’
,..............................................5’
令![]() ,但
,但![]() ,所以取
,所以取![]()
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减.
单调递减.
所以![]() ,此时
,此时![]() ...............................8’
...............................8’
②由![]() ,.......................................9’
,.......................................9’
此时的底面积为![]() (
(![]() ).......10’
).......10’
这个二次函数开口向上且对称轴![]() ,可知
,可知![]() 在
在![]() 上单调递减
上单调递减
所以![]() 时,可使
时,可使![]() 为最大.....................................12’
为最大.....................................12’
21. 解:① 设![]()
![]()
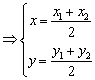 ........1’
........1’
由![]() ,易得右焦点
,易得右焦点![]() ....................2’
....................2’
当直线![]() 轴时,直线
轴时,直线![]() 的方程是:
的方程是:![]() ,根据对称性可知
,根据对称性可知![]() ......3’
......3’
当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]()
代入E有![]()
![]() ;
; ![]() ........................5’
........................5’
于是![]()
![]()
![]() ;
; ![]()
消去参数![]() 得
得![]()
而![]() 也适上式,故R的轨迹方程是
也适上式,故R的轨迹方程是![]() ...............8’
...............8’
②设椭圆另一个焦点为![]() ,
,
在![]() 中
中![]() 设
设![]() ,则
,则![]()
由余弦定理得![]()
![]() ............9’
............9’
同理,在![]() ,设
,设![]() ,则
,则![]()
也由余弦定理得![]()
![]() ............11’
............11’
于是![]() .........................12’
.........................12’
注:其它方法相应给分.
22.解:①![]() ....................3’
....................3’
由于当![]() 时
时![]() ,
,
所以![]() ,故
,故![]() 在
在![]() 上是增函数.......................6’
上是增函数.......................6’
②当![]() 时,并由①得
时,并由①得
![]() .................................7’
.................................7’
![]()
![]() ...............................................................................9’
...............................................................................9’
![]()
![]() ................................11’
................................11’
同理![]() ............................................................................................................12’
............................................................................................................12’
于是![]()
从而有![]() .........................................14’
.........................................14’