高三理复（一.二）数学周考试题2

高三理复（一.二）数学周考试题2

温馨提示：“知之者不如好之者，好之者不如乐之者。”

一、选择题：

1．若复数z满足i (1+2i) z = 5，则z等于

　　A．2－i　 　　　B．－2+i　 　　　C．－2－i　　　 D．－1－2i

2．设某等差数列的首项为a (a≠0)，第二项为b．则这个数列中有一项为0的充要条件是

A．a－b是正整数 B．a+b是正整数C．是正整数 D．是正整数

3．已知△ABC，若对任意t∈R，≥，则

A．∠A=90⁰　　 B．∠B＝90⁰　　 C．∠C＝90⁰　　 D．∠A＝∠B＝∠C＝60⁰

4．如图，一条螺旋线是用以下方法画成：△ABC是边长为1的正三角形，曲线CA₁，A₁A₂，A₂A₃分别以A、B、C为圆心，AC、BA₁、CA₂为半径画的圆弧，曲线CA₁A₂A₃称为螺旋线旋转一圈．然后又以A为圆心AA₃为半径画圆弧……这样画到第n圈，则所得螺旋线的长度l_n为

A．(3n²+n)　　　　　 B．(3n²－n+1)

C．　　　　 D．

5．已知三棱锥S－ABC的底面是正三角形，点A在侧面SBC上的射影H是△SBC的垂心，SA=a，则此三棱锥体积最大值是

　　 A．　　　　 B.　　　　　 C.　　　　　　　 D.

6．在△ABC中，若，则△ABC是　　　　　　　　　　　　　　　　　　　　　

　　　　A．等腰三角形　　　　　　　　B．正三角形　　　　　　　　　 C．直角三角形　　　　　　　 D．等腰直角三角形

7．已知函数f (x) = 3sin，g(x) = 3cos．若对任意x∈R都有，则g ()的值为　A．0　　　　　  　B．3　　　　　  C．－3 　　　D．3或－3

8．数列{a _n}的前n项和为S _n，且，则数列{a _n}的首项为

A．1或一2　　　　B．土1　　　　  C．土2　　　D．2或－1

9．椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.今有一个水平放置的椭圆形台球盘,点A、B是它的焦点,长轴长为2a,焦距为2c,静放在点A的小球(小球的半径忽略不计)从点A沿直线出发,经椭圆壁反射后第一次回到点A时,小球经过的路程是

A.4a　　 B.2(a－c)　　  C.2(a+c)　　 D.4a或2(a－c)或2(a+c)

10．已知定义在R上的减函数f (x)，对任意t∈R，总有f (－1+t)+f (－1－t)= 2．若m+n<－2，则

A．f (m)－f (n)>2　　B．f (m) + f (n)>2　 C．f (m)－f (n)<2　  D．f (m) + f (n)<2

11. 动点P为椭圆上异于椭圆顶点的一点，F₁、F₂为椭圆的两个焦点，动圆C与线段F₁P、F₁F₂的延长线及线段PF₂相切，则圆心C的轨迹为除去坐标轴上的点的

A一条直线　　B 双曲线的右支 C 抛物线　　　D 椭圆

12. 一次研究性课堂上，老师给出函数，三位同学甲、乙、丙在研究此函数时分别给出命题： 甲：函数的值域为；乙：若，则一定有；丙：若规定，则对任意恒成立.你认为上述三个命题中正确的个数有

A.0个　　　B.1个　　　 C.2个　　　 D.3个

二、填空题：

13．已知cos= a ，sin= 4sin(+)，则tan(+) =_______________.

14．已知每条棱长都为3的直平行六面体ABCD—A₁B₁C₁D₁中，∠BAD=60°，长为2的线段MN的一个端点M在DD₁上运动，另一个端点N在底面ABCD上运动.则MN中点P的轨迹与直平行六面体的表面所围成的较小的几何体的体积为_____　　　______.　

15．如图，某人从A出发沿道路逆时针行走再回到A，且所走过

的路线是一个矩形，则不同的走法有________种；若从B出发

按同样要求回到B，则不同的走法有__________种.　

16. 已知A(3，7)、B(－2，5)，线段AC、BC的中点都在坐标轴上，则C的坐标为__________.

三、解答题

17．已知函数f (x) = cos (+a) (0<<)的图象向右平移a个单位后得到的图象关于点(a+1，0)对称，且f (x)在[，1]上是单调函数，f(x)的图象关于点(4，0)对称，求f (x)的表达式．

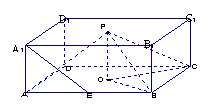
18.如图，O，P分别是正四棱柱ABCD－A₁B₁C₁D₁底面中心，E是AB的中点，AB=kAA₁，(Ⅰ)求证：A₁E∥平面PBC；（Ⅱ）当k＝时，求直线PA与平面PBC所成角的大小；(Ⅲ) 当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？

19.已知函数f(x)=x³+ax²+bx+c关于点(1,1)成中心对称，且f '(1)=0．（Ⅰ)求函数f(x)的表达式；

（Ⅱ)设数列{a_n}满足条件：a₁∈(1,2)，a_n+1=f (a_n) 求证：(a₁－ a₂)·(a₃－1)+(a₂－ a₃)·(a₄－1)+…+(a_n－ a_n+1)·(a_n+2－1)＜1

20有一种密码，明文是由三个字符组成.密码是由明文对应的五个数字组成，编码规则如下表：明文由表中每一排各取一个字符组成，且第一排取的字符放在第一位，第二排取的字符放在第二位，第三排取的字符放在第三位，对应的密码由明文对应的数字按相同的次序排成一排组成.

第一排	明文字符	A	B	C	D
	密码字符	11	12	13	14
第二排	明文字符	E	F	G	H
	密码字符	21	22	23	24
第三排	明文字符	M	N	P	Q
	密码字符	1	2	3	4

　设随机变量表示密码中不同数字的个数.（Ⅰ）求； （Ⅱ）求随机变量的分布列和它的数学期望.

21.设椭圆的焦点分别为，右准线交轴于点A，且.

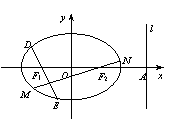（Ⅰ）试求椭圆的方程；（Ⅱ）过、分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点（如图所示），试求四边形DMEN面积的最大值.

　

22. 已知函数f(x)是在（0,+∞）上每一点处可导的函数，若xf′(x)＞f(x)在x＞0上恒成立.

（1.）求证：函数g(x)=（2）.当x₁＞0,x₂＞0时，证明：f(x₁)+f(x₂)＜f(x₁+x₂)。（3）.已知不等式ln(1+x)＜x在x＞-1且x≠0时恒成立，求证：…+N₊).

一、选择题

1．C　2．D　3．C　4．A　5．D　6．C　7．A　8．A　9．D　10．B

11. 提示：如图画出圆M，切点分别为E、D、G，由切线长相等定理知

　F₁G=F₁E，PD=PE，F₂D=F₂G，

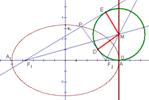　根据椭圆的定义知 PF₁+PF₂=2a，

　∴ PF₁+PF₂=F₁E+DF₂　(PD=PE)

　　 =F₁G+F₂D (F₁G=F₁E)

　　 = F₁G+F₂G=2a，

　∴ 2F₂G=2a－2c，F₂G=a－c，

　即点G与点A重合，∴ 点M在x轴上的射影是长轴端点A，

M点的轨迹是垂直于x 轴的一条直线（除去A点）

12.D

二、填空题

　13．　　14．　 15．30，94

提示：

2．D　是正整数．故选D．　

4．A　．

6．C

7．A　f ² (x)+g ² (x)=9，由已知是函数f (x)图象的对称轴，f()=3或f()=－3，g()=0，故选A．

8．A　a _l = 2 (a _l+a ₂)+a₁²得 a _l=1或－2．

9．分析:本题属信息迁移题,考查学生灵活应用知识的能力.

解:设靠近A的长轴端点为M，另一长轴的端点为N.若小球沿AM方向运动,则路程应为2(a－c)；若小球沿ANM方向运动,则路程为2(a+c)；若小球不沿AM与AN方向运动,则路程应为4a.

答案:D

10．B　由已知得f[－1+(n+1)]+f[－1－(n+1)]=2，即f (－2－n)=2－f(n)，由于

　　 m <－2一n，所以 f (m)>f(－2－n)=2－f(n)，即 f m)+f(n)>2．

13．　sin= sin [(+)－]=…= 4sin(+) 可化为．

15．30，94　横边、竖边各取一条与点A所在的横边、竖边可组成一个矩形，有6×5=30种；当B为矩形顶点时有5×6=30种，当B在横边上（不为顶点）时有5×2×4=40种，当B在纵边上(不为顶点)时有6×1×4=24种，共有30+40+24—94种．

16. 解析:设C的坐标为C(x,y)，则AC中点为M(,),BC中点为N(,).

∵≠,≠,且AC、BC的中点M、N都在坐标轴上，

∴M、N不在同一坐标轴上.

当M在x轴上、N在y轴上时，y_N==0,x_M==0,

即x=2,y=－7；

当M在y轴上、N在x轴上时，x_M==0,y_N==0,

即x=－3,y=－5.

∴C点坐标为(－3，－5)或(2，－7).

答案:(－3，－5)或(2，－7)

17．解：由题设y=cos[(x－a)+]的图象关于点(a+l，0)对称，

则cos[(a+1－a)+]=0，即 (k∈Z)．……………………3分

  又f (x) =cos(x+)在[，1]上是单调函数，

  令t=x+，则g(t)= cos t在[0，+]上是单调函数，

  ∴0<≤，∴0<k+≤1．

  ∵k∈Z，∴k=0，于是　+=………………………………………8分

  又f (x) =cos(x+)的图象关于点(4，0)对称，

  ∴4+ (m∈Z)，∴(m∈Z)．　　……………… 11分

∵0<<，∴，∴f(x)=cos()．……………………………12分

18. 解法一：

 (Ⅰ) 过P作MN∥B₁C₁，分别交A₁B₁、D₁C₁于M、N，则M、N A₁B₁、D₁C₁的中点，连MB，NC由四边形BCNM是平行四边形，　　　　　　 ∵E、M分别为AB、A₁B₁中点，∴A₁E∥MB

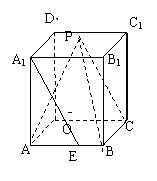又MB平面PBC，∴A₁E∥平面PBC。　　　　　 (Ⅱ)  过A作AF⊥MB，垂足为F，连PF，

∵BC⊥平面ABB₁A₁，AF平面ABB₁A₁，

∴AF⊥BC， BC∩MB=B，∴AF⊥平面PBC，

∴∠APF就是直线AP与平面PBC所成的角，  设AA₁=a，则AB=a，AF=，AP=，sin∠APF=

所以，直线AP与平面PBC所成的角是arcsin。　　　　　 （Ⅲ）连OP、OB、OC，则OP⊥BC，由三垂线定理易得OB⊥PC，OC⊥PB，所以O在平面PBC中的射影是△PBC的垂心，又O在平面PBC中的射影是△PBC的重心，则△PBC为正三角形。即PB=PC=BC　　　　　　　　　　　　　　　  所以k=。

反之，当k=时，PA=AB=PB=PC=BC，所以三棱锥为正三棱锥，

∴O在平面PBC内的射影为的重心　　　　　　　　   解法二：（建立空间坐标系）

19. 解：(Ⅰ)由f(x)=x³+ax²+bx+c关于点(1,1)成中心对称，所以

　　　　x³+ax²+bx+c+(2－x)³+a(2－x)²+b(2－x)+c=2　　　　　　　

对一切实数x恒成立．得：a=－3，b+c=3，

对由f '(1)=0，得b=3，c=0，

故所求的表达式为：f(x)= x³－3x²+3x．　　　　　　　　　　 

(Ⅱ) a_n+1=f (a_n)= a_n ³－3 a_n ²+3 a_n　　(1)

令b_n=a_n－1，0<b_n<1，由代入(1)得：b_n+1=，b_n=，∴ 1＞b_n ＞b_n+1 ＞0

　  (a₁－a₂)·(a₃－1)+(a₂－a₃)·(a₄－1)+…+(a_n－a_n+1)·(a_n+2－1)=

＜=b₁-b_n+1＜b₁＜1。　　　　　　　　　 

 （本题证法较多，其它证明方法得分可参照以上评分标准分步给分）

20. 解：（Ⅰ）密码中不同数字的个数为2的事件为密码中只有两个数字,注意到密码的第1,2列分别总是1,2,即只能取表格第1,2列中的数字作为密码.

.　　　　　　　　　　　　　  ……………………………4分

（Ⅱ）由题意可知,的取值为2,3,4三种情形.

若,注意到表格的第一排总含有数字1,第二排总含有数字2则密码中只可能取数字1,2,3或1,2,4.

.

若,则

(或用求得).　　　　　　　　 ……………………………8分

的分布列为：

	2	3	4

　.　　　　……………………………12分

21. 解（Ⅰ）由题意，， ∴，　　　　 2分

∵　∴为A的中点　　　　　　 3分

∴，　　　　　　　　　　　　　　

即　 椭圆方程为.　　　　　　　　  5分

（Ⅱ）当直线DE与轴垂直时，，

此时，四边形的面积为.

同理当MN与轴垂直时，也有四边形的面积为.　　　当直线DE，MN均与轴不垂直时，设，代入椭圆方程，消去得：

.

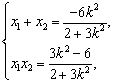设，，则　　　　　　 所以，，

所以，，

同理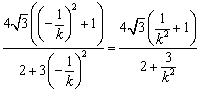，.　　　　　　 所以，四边形的面积==，

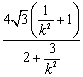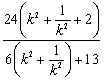令，得

因为，

当时，，且S是以为自变量的增函数，

所以

综上可知，即四边形DMEN面积的最大值为4，最小值为.　　

22. （1）证明：由g(x)=′(x)=

　　　由xf′（x）＞f(x)可知：g′(x) ＞0在x＞0上恒成立.

　　　从而g(x)=

　（2）由（1）知g(x)=

　　　在x₁＞0,x₂＞0时，　

于是f(x₁)＜

两式相加得到：f(x₁)+f(x₂)＜f(x₁+x₂)

（1）　　　　 由（2）中可知：g(x)=

　 由数学归纳法可知：x_i＞0(i=1,2,3,…,n)时,

有f(x₁)+f(x₂)+f(x₃)+… +f(x_n)＜f(x₁+x₂+x₃+…+x_n) (n≥2)恒成立.

设f(x)=xlnx，则在x_i＞0(i=1,2,3,…,n)时

有x₁lnx₁+x₂lnx₂+…+x_nlnx_n＜(x₁+x₂+…+x_n)ln(x₁+x₂+…+x_n)（n≥2）……（*）恒成立.

令x_n=…+x_n=…+

 由S_n＜…+

S_n＞…+

(x₁+x₂+…+x_n)ln(x₁+x₂+…+x_n)<(x₁+x₂+…+x_n)ln(1-…+x_n)(∵ln(1+x)＜x)

＜-　 (**)

由（**）代入（*）中，可知：

…+

于是：…+