高三理复班(一.二)数学周考试题
温馨提示:“知之者不如好之者,好之者不如乐之者。” (2007.01.05) 总分150分
一、选择题
1.已知复数z1=3+i,z2=1-i,则复数z1·z2的虚部为
(A)2i (B)-2i (C)2 (D)-2
2.不等式y≤3x+b所表示的区域恰好使点(3,4)不在此区域内,而点(4,4)在此区域内,则b的取值范围是
(A)-8≤b≤-5 (B)b≤-8或b>-5 (C)-8≤b<-5 (D)b≤-8或b≥-5
3.下列说法错误的是
(A)命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”
(B)“x=1”是“x2-3x+2=0”的充分不必要条件
(C)若pÙq为假命题,则p、q均为假命题
(D)对于命题p:“存在x∈R,使得x2+x+1<0”,则Øp:“任意x∈R,均有x2+x+1≥0”
4.已知等差数列{an}的前n项和为Sn,若m>1,m∈N*,且![]() ,则m等于
,则m等于
A.11 B.10 C.9 D.8
5.已知直线m、n和平面α、β,且m⊥α,nÌβ,给出下列四个命题:
①若α//β,则m⊥n; ②若m⊥n,则α//β;
③若α⊥β,则m//n; ④若m//n,则α⊥β.其中正确的命题是
(A)①④ (B)①③ (C)②③ (D)③④
6.已知定义在R上 的偶函数f(x)的单调递减区间为[0,+∞),则不等式f(x)<f(2-x)的解集是
(A)(1,2) (B)(1,+∞) (C)(2,+∞) (D)(-∞,1)
7.设椭圆的两个焦点为F1、F2,如果过点F1的直线被椭圆截得的最短线段MN的长为![]() ,且ΔMF2N的周长为20,则椭圆的离心率为 (A)
,且ΔMF2N的周长为20,则椭圆的离心率为 (A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.有下面四个命题: ①“x=2kπ+![]() (k∈Z)”是“tanx=
(k∈Z)”是“tanx=![]() ”的充分不必要条件;
”的充分不必要条件;
②函数f(x)=2cosx-1的最小正周期是π;③函数f(x)=sin(x+![]() )在[
)在[![]() ,
,![]() ]上是增函数;
]上是增函数;
④若函数f(x)=asinx-bcosx的图象的一条对称轴的方程为x=![]() ,则a+b=0.
,则a+b=0.
其中正确命题的个数是 (A)1 (B)2 (C)3 (D)4
9.已知![]() 点C在∠AOB内,且∠AOC=45°,设
点C在∠AOB内,且∠AOC=45°,设![]() 等于 A.
等于 A.![]() B.
B.![]() C.
C.![]() D.2
D.2
10.在直角三角形ABC中,∠C=90°,那么sinA·cos2(45°-![]() 为
为
A.有最大值![]() 和最小值0 B.有最大值
和最小值0 B.有最大值![]() ,但无最小值
,但无最小值
C.既无最大值也无最小值 D.有最大值![]() ,但无最小值
,但无最小值
11.为了解湖中养鱼的多少,某人在湖中打了一网鱼,共m条,做上记号后放入湖中,数日
后又打了一网鱼,共n条,其中k条鱼有记号,估计湖中有鱼
A.![]() 条 B.
条 B.![]() 条 C.m
条 C.m![]() D.无法估计
D.无法估计
12..正方体ABCD—A1B1C1D1的侧面ABB1A1内有一动点P到直线AA1和BC的距离相等,
则动点P的轨迹是
A.线段 B.抛物线的一部分 C.双曲线的一部分 D.椭圆的一部分
二、填空题:
13.已知可导函数f(x)的导函数为![]() ,且满足
,且满足![]() ,则
,则![]() .
.
14.把函数![]() 的图象沿向量
的图象沿向量![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 可以是__________。
可以是__________。
15.若正数![]() 满足
满足![]() ,则
,则![]() 的取值范围是__________。
的取值范围是__________。
16.设函数![]() 的定义域为
的定义域为![]() ,若存在常数
,若存在常数![]() ,使
,使![]() ≤
≤![]() 对一切实数
对一切实数![]() 均成立,则称
均成立,则称![]() 为
为![]() 函数。给出下列函数:
函数。给出下列函数:
①![]() ;②
;②![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() ;
;
⑤![]() 是R上的奇函数,且满足对一切实数
是R上的奇函数,且满足对一切实数![]() 、
、![]() 均有
均有![]() .
.
其中是![]() 函数的序号为 。
函数的序号为 。
三、解答题:
17. 在ΔABC中,已知![]()
(1)求证,a、b、c成等差数列; (2)求角B的取值范围。
18.在四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,AG=![]() GD,BG⊥GC,GB=GC=2,E是BC的中点. (Ⅰ)求异面直线GE与PC所成的角的余弦值;
GD,BG⊥GC,GB=GC=2,E是BC的中点. (Ⅰ)求异面直线GE与PC所成的角的余弦值;
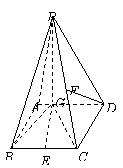 (Ⅱ)求点D到平面PBG的距离; (Ⅲ)若F点是棱PC上一点,且DF⊥GC,求
(Ⅱ)求点D到平面PBG的距离; (Ⅲ)若F点是棱PC上一点,且DF⊥GC,求![]() 的值.
的值.
19. 箱中装有15张大小、重量一样的卡片,每张卡片正面分别标有1到15中的一个号码,正面号码为![]() 的卡片反面标的数字是
的卡片反面标的数字是![]() .(卡片正反面用颜色区分)(1)如果任意取出一张卡片,试求正面数字大于反面数字的概率;(2)如果同时取出两张卡片,试求他们反面数字相同的概率.
.(卡片正反面用颜色区分)(1)如果任意取出一张卡片,试求正面数字大于反面数字的概率;(2)如果同时取出两张卡片,试求他们反面数字相同的概率.
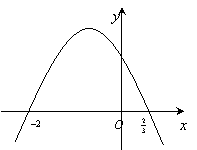
20.设![]() 的极小值为
的极小值为![]() ,其导函数
,其导函数![]() 的图像经过点
的图像经过点![]() ,如图所示,
,如图所示,
(1)求![]() 的解析式;
的解析式;![]() (2)若对
(2)若对![]() 都有
都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
 |
21已知P是椭圆C:![]() 上异于长轴端点的任意一点,A为长轴的左端点,F为椭圆的右焦点,椭圆的右准线与x轴、直线AP分别交于点K、M,
上异于长轴端点的任意一点,A为长轴的左端点,F为椭圆的右焦点,椭圆的右准线与x轴、直线AP分别交于点K、M,![]() .
.
(Ⅰ)若椭圆的焦距为6,求椭圆C的方程;
(Ⅱ)若![]() ,求证:
,求证:![]() .
.

22.数列![]() 中,
中,![]() (1)求数列
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() 为
为![]() 的前n项和,并且存在n,使
的前n项和,并且存在n,使![]() 与
与![]() 同时取得最小值,求
同时取得最小值,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,令
时,令![]()
参考答案
一、选择题:
1.(D) 2.(C) 3.(C) 4.(B) 5.(A) 6.(B) 7.(D) 8.(B)9(C)
10.(B) 11.(B) 12.(B)
二.填空题:(13)6、(14)![]() 、(15)
、(15)![]() 、(15)、(16)①②④⑤
、(15)、(16)①②④⑤
17. 解:(1)由条件得:![]()
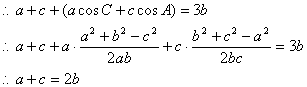
∴a、b、c成等差数列 ……6′
(2)![]()
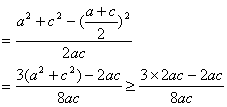
![]() ……10′
……10′
![]() ……12′
……12′
18.解:方法一:
(Ⅰ)解:以G点为原点,直线GB、GD、GP分别为x轴、y轴、z轴建立空间直角坐标系,则B(2,0,0),C(0,2,0),P(0,0,4), ……1分
故E(1,1,0),且![]() =(1,1,0),
=(1,1,0),![]() =(0,2,4). ……2分
=(0,2,4). ……2分
设直线GE与PC所成的角为θ,则
cosθ=![]() =
=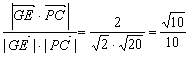 ,
,
所以GE与PC所成的角的余弦值为![]() . ……4分
. ……4分
(Ⅱ)解:平面PBG的一个法向量n=(0, 1,0). ……5分
又![]() , ……6分
, ……6分
所以点D到平面PBG的距离为![]() n =
n =![]() . ……8分
. ……8分
(Ⅲ)解:设F(0,y,z),则![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
解得y=![]() . ……10分
. ……10分
又F在PC上,所以可设![]() ,则(0,
,则(0,![]() ,z-4)=λ(0,2,-4),
,z-4)=λ(0,2,-4),
∴z=1. ……12分
故F(0,![]() ,1).
,1).
所以![]() ,
,
∴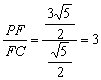 . ……14分
. ……14分
方法二:
(Ⅰ)在平面ABCD内,过C点作CH∥EG,交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角. ……2分
在△PCH中,CH=![]() ,PC=
,PC=![]() ,PH=
,PH=![]() ,
,
由余弦定理得,cos∠PCH=![]() .
.
所以GE与PC所成的角的余弦值为![]() . ……4分
. ……4分
(Ⅱ)∵PG⊥平面ABCD,PGÌ平面PBG,∴平面PBG⊥平面ABCD.
在平面ABCD内,过D作DK⊥BG,交BG延长线于K,则DK⊥平面PBG,所以DK的长就是点D到平面PBG的距离. ……6分
∵BC=![]() ,GD=
,GD=![]() AD=
AD=![]() BC=
BC=![]() ,
,
所以在△DKG中,DK=DGsin45°=![]() ,
,
∴点D到平面PBG的距离为![]() . ……8分
. ……8分
(Ⅲ)在面PGC内,过F作FM⊥GC于M,由平面PGC⊥平面ABCD,得FM⊥平面ABCD ,∴FM∥PG. ……10分
∵DF⊥GC,∴DM⊥GC,故GM=GD·cos45°=![]() . ……12分
. ……12分
所以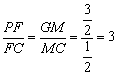 . ……14分
. ……14分
19.解:(1)由不等式![]() ,得
,得![]() ……(3分)
……(3分)
由题意知![]() ,即共有2张卡片正面数字大于反面数字,
,即共有2张卡片正面数字大于反面数字,
故所求的概率为![]() .
.
答:所求的概率为![]() .
……(6分)
.
……(6分)
(2)设取出的是第![]() 号卡片和
号卡片和![]() 号卡片(
号卡片(![]() ),
),
则有![]() ……(8分)
……(8分)
即![]() ,由
,由![]() 得
得![]() ……(10分)
……(10分)
故符合条件的取法为1,11;2,10;3,9;4,8;5,7.
故所求的概率为![]() .
.
答:故所求的概率为![]() .
……(12分)
.
……(12分)
20. 解:(1)![]() ,且
,且![]() 的图像经过点
的图像经过点![]() ,
,
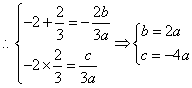 ,
……(2分)
,
……(2分)
![]() ,
,
由图像可知函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
在![]() 上单调递减,
……(3分)
上单调递减,
……(3分)
∴![]() ,解得
,解得![]() ……(5分)
……(5分)
∴![]() ……(6分)
……(6分)
(2)要使对![]() 都有
都有![]() 恒成立,
恒成立,
只需![]() 即可.
……(7分)
即可.
……(7分)
由(1)可知函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
在![]() 上单调递减,
上单调递减,
且![]() ,
,![]() ,
,
![]() ……(10分)
……(10分)
![]()
故所求的实数![]() 的取值范围为
的取值范围为![]() .
……(12分)
.
……(12分)
21. (Ⅰ)解一:由![]() 得,
得,![]() ,
,![]() ,………………………2分
,………………………2分
∴ ![]() ,…………………………………………………………………4分
,…………………………………………………………………4分
从而椭圆方程是![]() .…………………………………………………………6分
.…………………………………………………………6分
解二:记![]() ,由
,由![]() ,
,
得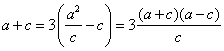 ,
,
∵![]() ,∴
,∴ ![]() ,………………………………………………………2分
,………………………………………………………2分
又![]() ,
,![]() ,∴
,∴ ![]() ,…………………………………………4分
,…………………………………………4分
从而椭圆方程是![]() . ………………………………………………………6分
. ………………………………………………………6分
(Ⅱ)解一:点![]() 同时满足
同时满足
![]() 和
和![]()
消去![]() 并整理得:
并整理得:![]() ,此方程必有两实根,一根是点
,此方程必有两实根,一根是点![]() 的模坐标
的模坐标![]() ,另一根是点
,另一根是点![]() 的模坐标
的模坐标![]() ,
,
![]() ,
,![]() ,
,
∴ ![]() ,
,
![]()
∴ ![]() ,
,
由![]() 代入上式可得
代入上式可得![]() .
.
∴ ![]() .
.![]() .
.
解二:由(Ⅰ)![]() ,
,![]() ,可设
,可设![]() ,
,![]() ,则
,则![]() ,
,
椭圆方程可为![]() ,即
,即![]() ,
,
设直线AM的方程为![]() (
(![]() 存在且
存在且![]() ),
),
代入![]() ,
,
整理得![]() ,
,
此方程两根为A、P两点的横坐标,
由韦达定理![]() ,
,![]()
∴ ![]() ,从而
,从而![]() .
.
由于![]()
![]() =
=![]()
![]() ,
,![]() ,
,
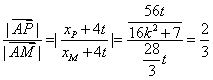
∴ ![]() .
.![]() .
.
22. (1)∵![]()
∴![]()
两式相减得![]()
∴{an}的奇数项与偶数项分别构成公差为3的等差数列,
当n为奇数时,![]()
当n为偶数时,![]()
∴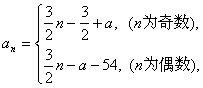
(2)当n为偶数时,∵![]()
∴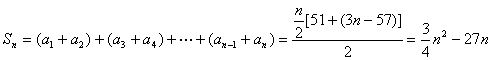
当n为奇数时,
![]()
若n为偶数,则![]() ;
;
若n为奇数,则![]()
∵![]() 在n=18时取得最小值,
在n=18时取得最小值,
∴对于任意的n∈N*,![]()
∴![]()
(3)当![]()
![]()
∴![]()
![]()