高三理复班数学备考精选试题集(1)

　　高三理复班数学备考精选试题集(1)

1．在△ABC中，a、b、c分别为角A、B、C的对边，，则△ABC的形状为（　B  ）

　　　　A．正三角形　　　　　　　　　B．直角三角形　　　　 C．等腰直角三角形　　　　　 D．等腰三角形或直角三角形

2.“”是“”的　　 条件。（答：充分非必要条件）

3．已知平面上三点A、B、C满足的值等于　　　　　　　　　　　　　　（　 C ）A．25　　B．24 C．－25　 D．－24

4. 函数f（x）＝x²－a 在区间［－1，1］上的最大值M（a）的最小值是  A．　 B．　　  C．1　　D．2

【解析】选B．f（x）是偶函数，所以M（a）是在［0，1］内的最大值，当a≤0时，f（x）＝x²－a，则M（a）＝1－a；当a>0时，由图像可知，若，则M（a）＝a，若，则M（a）＝f（1）＝1－a，从而M（a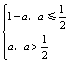）＝ ，　  M（a）_min＝．

5、已知两圆方程分别为：，，则两圆的公切线方程为（A）

A、　　B、　　C、　　  D、

6、对正整数，设抛物线，过任作直线交抛物线于，两点，则数列的前项和为__—n(n+1)________

7．正实数x₁，x₂及函数，f (x)满足，则的最小值为（ B　 ）

　　　　 A．4　　　　　　　　　　　　　　　　 B．　　　　　　　　　　　　　　　　C．2　　　　　　　　　　　　　　　　 D．

8．已知双曲线的左右两焦点分别为，是双曲线右支上的一点， 点满足，在上的投影的大小恰为，且它们的夹角为，则等于

A．　 　　　B．　 　　 C．　　　 D．

【解析】因为，所以是一对同向向量，且．

又因为在上的投影的大小恰为，所以．

在中，又，

所以，所以，故选A．

9．已知f （x）＝x＋1，g （x）＝2x＋1，数列{a_n}满足：a₁＝1，a_n＋1＝则数列{a_n}的前2007项的和为A．5×2²⁰⁰⁸－2008　　　　 　B．3×2²⁰⁰⁷－5020　 C．6×2²⁰⁰⁶－5020　　 D．6×2¹⁰⁰³－5020

【解析】∵a_2n＋2＝a_2n＋1＋1＝（2a_2n＋1）＋1＝2a_2n＋2，∴a_2n＋2＋2＝＝2（a_2n＋2），

∴数列{a_2n＋2}是以2为公比、以a₂＝a₁＋1＝2为首项的等比数列．

∴a_2n＋2＝2×2 ^n－1，∴a_2n＝2 ⁿ－2．

又a_2n＋a_2n＋1＝ a_2n＋2a_2n＋1＝3a_2n＋1，∴数列{a_n}的前2007项的和为

a₁＋（ a₂＋ a₃）＋ （ a₄＋ a₅）＋ （ a₆＋ a₇）＋ …＋ （ a₂₀₀₆＋ a₂₀₀₇）

＝ a₁＋（3a₂＋1）＋ （3a₄＋1）＋ （3a₆＋1）＋ …＋ （3a₂₀₀₆＋1）

＝ 1＋（3×2－5）＋ （3×2²－5）＋ （3×2³－5）＋ …＋ （3×2¹⁰⁰³－5）

＝ 1＋（3×2－5）＋ （3×2²－5）＋ （3×2³－5）＋ …＋ （3×2¹⁰⁰³－5）

＝ 3×（2＋2²＋2³＋…＋2¹⁰⁰³＋1－5×1003

＝6×（2¹⁰⁰³－1）＋1－5×1003＝6×2¹⁰⁰³－ 5020 ，故选D．

10. 在△ABC中，E、F分别为AB、AC上的点，若=m，=n，则= mn. 拓展到空间：在三棱锥S-ABC中，D、E、F分别是侧棱SA、SB、SC上的点，若= m，=n，= p，则=

11．已知△ABC，若对任意t∈R，≥，则C

A．∠A=90⁰　　 B．∠B＝90⁰　　 C．∠C＝90⁰　　 D．∠A＝∠B＝∠C＝60⁰

12．等差数列的前项和为，公差. 若存在正整数，使得，则当（）时，有（填“>”、“<”、“=”）．  

※设等差数列{a_n}的前n项和为S_n，已知S₁₂＞0，S₁₃＜0，则 ，，…， 中最大的是　B

　　(A) 　　　　　  (B) 　　　　　  (C) 　　　　　  (D)

13．定义在N*上的函数满足：f(0) = 2，f(1) = 3，且．

（Ⅰ）求f(n)（nÎN*）；（Ⅱ）求．

解（Ⅰ）由题意：，所以有：，又，所以，即故．

（Ⅱ）．

14．已知函数f(x)=x³+ax²+bx+c关于点(1,1)成中心对称，且f '(1)=0．（Ⅰ)求函数f(x)的表达式；

　（Ⅱ)设数列{a_n}满足条件：a₁∈(1,2)，a_n+1=f (a_n) 求证：(a₁－ a₂)·(a₃－1)+(a₂－ a₃)·(a₄－1)+…+(a_n－ a_n+1)·(a_n+2－1)＜1

解：(Ⅰ)由f(x)=x³+ax²+bx+c关于点(1,1)成中心对称，所以x³+ax²+bx+c+(2－x)³+a(2－x)²+b(2－x)+c=2　　　　　　

对一切实数x恒成立．得：a=－3，b+c=3，对由f '(1)=0，得b=3，c=0，故所求的表达式为：f(x)= x³－3x²+3x．(Ⅱ) a_n+1=f (a_n)= a_n ³－3 a_n ²+3 a_n　　(1)令b_n=a_n－1，0<b_n<1，由代入(1)得：b_n+1=，b_n=，

∴ 1＞b_n ＞b_n+1 ＞0 (a₁－a₂)·(a₃－1)+(a₂－a₃)·(a₄－1)+…+(a_n－a_n+1)·(a_n+2－1)=

＜=b₁-b_n+1＜b₁＜1。　　　　　　　 　 

15.已知O为坐标原点，点E、F的坐标分别为（-1，0）、（1，0），动点A、M、N满足（），，，．（Ⅰ）求点M的轨迹W的方程；（Ⅱ）点在轨迹W上，直线PF交轨迹W于点Q，且，若，求实数的范围．

解：（Ⅰ）∵，，∴ MN垂直平分AF．又，∴ 点M在AE上，

∴ ，，∴ ，　　∴ 点M的轨迹W是以E、F为焦点的椭圆，且半长轴，半焦距，∴ ．

∴ 点M的轨迹W的方程为（）．

（Ⅱ）设∵ ，，∴ 　　 ∴ 　

由点P、Q均在椭圆W上，

∴ 　　消去并整理，得，由及，解得．　　

16已知函数的定义域为，导数满足0＜＜2　且，常数为方程的实数根，常数为方程的实数根．（Ⅰ）若对任意，存在，使等式成立．试问：方程有几个实数根；（Ⅱ）求证：当时，总有成立；（Ⅲ）对任意，若满足，求证：。

解：（I）假设方程有异于的实根m，即．则有成立 ．因为，所以必有，但这与≠1矛盾，因此方程不存在异于c₁的实数根．∴方程只有一个实数根．

（II）令，∴函数为减函数．又，

∴当时，，即成立．

（III）不妨设，为增函数，即．又，∴函数为减函数即．，即．，．

17．设无穷数列{a_n}具有以下性质：①a₁=1；②当（Ⅰ）请给出一个具有这种性质的无穷数列，使得不等式 对于任意的都成立，并对你给出的结果进行验证（或证明）；（Ⅱ）若，其中，且记数列{b_n}的前n项和B_n，证明：

解：（Ⅰ）令，则无穷数列{a_n}可由a₁ = 1，给出.

　　显然，该数列满足，且  

　 （Ⅱ）  又

　　    

18．已知△ABC中，三个内角是A、B、C的对边分别是a、b、c，其中c=10，且

　　　　（I）求证：△ABC是直角三角形；（II）设圆O过A、B、C三点，点P位于劣弧AC上，∠PAB=60°,.求四边形ABCP的面积.

解：（Ⅰ）证明：根据正弦定理得，

整理为，sinAcosA=sinBcosB，即sin2A=sin2B.

∴2A=2B或2A+2B=　 ∴.

　∴舍去A=B.　 ∴即.故△ABC是直角三角形.

（Ⅱ）解：由（1）可得：a=6，b=8.在Rt△ACB中，

∴ ==

连结PB，在Rt△APB中，AP=AB·cos∠PAB=5.

∴四边形ABCP的面积=24+=18+.

19已知集合．（1）求；（2）若以为首项，为公比的等比数列前项和记为，对于任意的，均有，求的取值范围．

【解析】（1）由得

当时，．当时， ，当时，．综上，时，；时，；当时， ．

（2）当时，．而，故时，不存在满足条件的；

当时，，而是关于的增函数，所以随的增大而增大，当且无限接近时，对任意的，，只须满足 解得． 当时，．显然，故不存在实数满足条件．　当时，．，适合．当时，．

，

，

，且故．

故只需 即 解得．综上所述，的取值范围是．

20设一动点M在x轴正半轴上，过动点M与定点的直线交y＝x（x>0）于点Q，动点M在什么位置时，有最大值，并求出这个最大值．

【解析】 设，要它与相交，则．

　　　令，令，得． ∴．

　　 ∴于是．由，∴．而当l的方程为x＝2时，u＝2， ∴对应得k＝－2， ．

不管什么时候，自己才是自己的天使，要笑着去面对生活！记住阳光总在风雨后，高考过后，你的天空会是另一番的精彩！