高三理科数学模拟试卷
Y本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.全卷满分为150分,考试时间为120分钟。第I卷为选择题,共60分;第Ⅱ卷共90分,包括填空题和解答题两种题型.
第I卷
一、选择题(共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请用铅笔把答题卡上对应题目的答案标号涂黑)
1.若集合![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
1.A ![]() , 而
, 而![]() ,
,
得![]()
2.设![]() 则
则![]() 的关系是( )
的关系是( )
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
2.A ![]()
3.下列命题中的真命题是( )
A.![]() 是有理数 B.
是有理数 B.![]() 是实数
是实数
C.![]() 是有理数 D.集合
是有理数 D.集合![]() 是实数集
是实数集![]() 的真子集
的真子集
3.B ![]() 属于无理数指数幂,结果是个实数;
属于无理数指数幂,结果是个实数;![]() 和
和![]() 都是无理数;
都是无理数;![]()
4.若![]() 且
且![]() 则
则![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.B 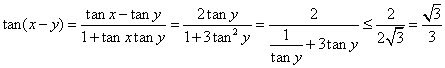
而![]() ,
,![]()
5.已知向量![]() ,向量
,向量![]() ,则
,则![]() 的最大值,
的最大值,
最小值分别是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.D ![]()
![]() ,最大值为
,最大值为![]() ,最小值为
,最小值为![]()
或结合向量的几何意义使用数形结合来做
6.在等差数列![]() 中,若
中,若![]() ,
,
则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.A ![]() 而
而![]() 成等差数列
成等差数列
即![]()
![]()
7.过圆![]() 外一点
外一点![]() ,引圆的两条切线,切点为
,引圆的两条切线,切点为![]() ,
,
则直线![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.B.设切点为![]() ,则
,则![]() 的方程为
的方程为![]()
![]() 的方程为
的方程为![]() ,则
,则![]()
![]()
![]()
8.若抛物线![]() 上一点
上一点![]() 到准线的距离等于它到顶点的距离,则点
到准线的距离等于它到顶点的距离,则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.B 点![]() 到准线的距离即点
到准线的距离即点![]() 到焦点的距离,得
到焦点的距离,得![]() ,过点
,过点![]() 所作的高也是中线
所作的高也是中线
![]() ,代入到
,代入到![]() 得
得![]() ,
,![]()
9.在正三棱锥![]() (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,![]() ,过
,过![]() 作与
作与![]() 分别交于
分别交于![]() 和
和![]() 的截面,则截面
的截面,则截面![]()
![]() 的周长的最小值为( )
的周长的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.C沿着![]() 将正三棱锥
将正三棱锥![]() 侧面展开,则
侧面展开,则![]() 共线,且
共线,且![]() ,利用三角形相似,得
,利用三角形相似,得![]()
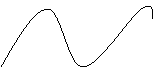
10.如图是函数![]() 的大致图象,则
的大致图象,则![]() 等于(
)
等于(
)
![]()
![]()
|
|
|
|
10.C 函数![]() 图象过点
图象过点![]() ,得
,得![]()
![]() ,则
,则![]() ,
,![]() ,且
,且![]() 是
是
函数![]() 的两个极值点,即
的两个极值点,即![]() 是方程
是方程![]() 的实根
的实根
![]()
11.关于![]() 的方程
的方程![]() 有实根的充要条件是( )
有实根的充要条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.D 令![]() ,则原方程变为
,则原方程变为![]() ,
,
方程![]() 有实根的充要条件是方程
有实根的充要条件是方程![]() 在
在![]() 上有实根
上有实根
再令![]() ,其对称轴
,其对称轴![]() ,则方程
,则方程![]() 在
在![]() 上有一实根,
上有一实根,
另一根在![]() 以外,因而舍去,即
以外,因而舍去,即![]()
12.在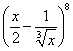 的展开式中的常数项是( )
的展开式中的常数项是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.A ![]()
令![]()
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上.)
13.若函数![]() ,且
,且![]() 则
则![]() ___________。
___________。
13.![]() 显然
显然![]() ,令
,令![]() 为奇函数
为奇函数
![]()
或者13. 函数![]() 在区间
在区间![]() 上的最大值是
。
上的最大值是
。
13.![]()
![]() ,比较
,比较![]() 处的函数值,得
处的函数值,得![]()
14. 在![]() 件产品
件产品![]() 中有
中有![]() 件是次品,从中任意抽了
件是次品,从中任意抽了![]() 件,至少有
件,至少有![]() 件是次品的抽法共有______________种(用数字作答).
件是次品的抽法共有______________种(用数字作答).
14. ![]()
![]() 件次品,或
件次品,或![]() 件次品,
件次品,![]()
15. 下列各数![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() ,其中最小的数是____________。
,其中最小的数是____________。
15. ![]()
![]() 、
、 ![]() 、
、
![]() 、
、 ![]()
16.不等式![]() 的解集是_______________。
的解集是_______________。
16.![]()
![]()
![]()
![]()
三.解答题:
17.(本题满分12分)平面向量![]() ,若存在不同时为
,若存在不同时为![]() 的实数
的实数![]() 和
和![]() ,使
,使![]() 且
且![]() ,
,
(1)试求函数关系式![]() ;
;
(2)并求该函数![]() 的单调递增区间.
的单调递增区间.
17解:(1)由![]() 得
得![]()
![]()
![]()
(2)![]() ,
,![]()
令![]() ,得
,得![]()
所以单调递增区间为![]()
18.(本题满分12分)求和:![]()
18.解:记![]() 当
当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]()
![]()
∴原式=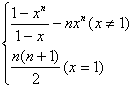
19.(本题满分12分)甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为![]() ,被甲或乙解出的概率为
,被甲或乙解出的概率为![]() ,(1)求该题被乙独立解出的概率;(2)求解出该题的人数
,(1)求该题被乙独立解出的概率;(2)求解出该题的人数![]() 的数学期望和方差
的数学期望和方差
19.解:(1)记甲、乙分别解出此题的事件记为![]() .
.
设甲独立解出此题的概率为![]() ,乙为
,乙为![]() .
.
则![]()
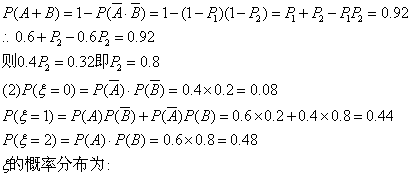
|
|
|
|
|
|
|
|
|
|
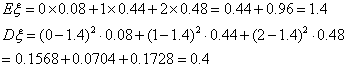
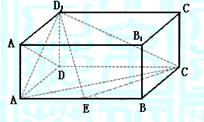
20.(本题满分14分)如图,在长方体![]() ,中,
,中,![]() ,点
,点![]() 在棱
在棱![]() 上移动.(1)证明:
上移动.(1)证明:![]() ;
;
(2)当![]() 为
为![]() 的中点时,求点
的中点时,求点![]() 到面
到面![]() 的距离;
的距离;
(3)![]() 等于何值时,二面角
等于何值时,二面角![]() 的大小为
的大小为![]() .
.
|
20.解:以![]() 为坐标原点,直线
为坐标原点,直线![]() 分别为
分别为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,则
,则![]()
(1)![]()
(2)因为![]() 为
为![]() 的中点,则
的中点,则![]() ,从而
,从而![]() ,
,
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则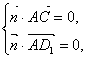
也即![]() ,得
,得![]() ,从而
,从而![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离为
的距离为
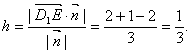
(3)设平面![]() 的法向量
的法向量![]() ,∴
,∴![]()
由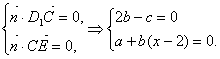 令
令![]() ,
,
∴![]()
依题意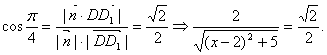
∴![]() (不合,舍去),
(不合,舍去),![]() .
.
∴![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.
21.(本题满分14分)已知椭圆![]() ,试确定
,试确定![]() 的值,使得在此椭圆上存在不同
的值,使得在此椭圆上存在不同
两点关于直线![]() 对称。
对称。
21.解:设![]() ,
,![]() 的中点
的中点![]() ,
,![]()
而![]()
![]() 相减得
相减得![]()
即![]() ,
,![]()
而![]() 在椭圆内部,则
在椭圆内部,则![]() 即
即![]() 。
。
四.选答题:(10分,从下列三题中选答一题,多选则去掉一个得分最低的题后计算总分)
22.过点![]() 作倾斜角为
作倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于点
交于点![]() ,
,
求![]() 的值及相应的
的值及相应的![]() 的值。
的值。
22.解:设直线为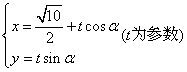 ,代入曲线并整理得
,代入曲线并整理得
![]()
则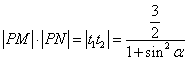
所以当![]() 时,即
时,即![]() ,
,![]() 的最小值为
的最小值为![]() ,此时
,此时![]() 。
。
23.已知![]() ,且
,且![]()
求证:![]()
23.证明:显然![]()
![]() 是方程
是方程![]() 的两个实根,
的两个实根,
由![]() 得
得![]() ,同理可得
,同理可得![]() ,
,![]()
 24.如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过Q作⊙O的切线交OA的延长线于R,求证:RP=RQ
24.如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任意一点,BP的延长线交⊙O于Q,过Q作⊙O的切线交OA的延长线于R,求证:RP=RQ
24.证明:连接OQ,∵OQ=OB
∴∠OBP=∠OQP
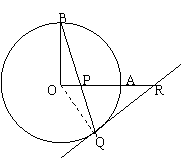 又∵QR为⊙O的切线
又∵QR为⊙O的切线
∴OQ⊥QR
即∠OQP+∠PQR= Rt∠
而∠OBP+∠OPB= Rt∠
故∠PQR=∠OPB
又∵∠OPB与∠QPR为对顶角
∴∠OPB=∠QPR
∴∠PQR=∠QPR
∴RP=RQ