高三理科数学试题(3)
总分150分
一、选择题(共50分)
1、已知等比数列![]() 的前n项和为
的前n项和为![]() ,则a16+ a17+ a18+ a19+ a20 =( )
,则a16+ a17+ a18+ a19+ a20 =( )
A、8 B、12 C、16 D、24
2、设复数![]() ,则
,则![]() 的展开式的第5项是( )
的展开式的第5项是( )
A、![]() B、35
C、
B、35
C、![]()
![]() D、
D、![]()
3、定义![]() 那么
那么![]() Tn的值为( )
Tn的值为( )
A、![]() B、1
C、
B、1
C、![]() D、0
D、0
4、已知![]()
![]() 的值为( )
的值为( )
A、![]() B、0
C、 5
D、与
B、0
C、 5
D、与![]() 的值有关
的值有关
5、设![]() ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6、定义在R上的函数![]() 不恒为零,且满足
不恒为零,且满足![]() ( )
( )
A、是奇函数,是也周期函数 B、是偶函数,是也周期函数
C、是奇函数,但不是周期函数 D、是偶函数,但不是周期函数
7、能够使圆C:![]() 上恰有两个点到直线
上恰有两个点到直线![]() 的距离等于1的
的距离等于1的![]() 的一个值是( )
的一个值是( )
A、2
B、![]() C、3
D、
C、3
D、![]()
8、某班新年联欢会原定的5 个节目已排成节目单,开演前又增加了两个节目,如果将这两个节目插入原节目单中,那么不同的插法种数是 ( )
A、42 B、30 C、20 D、12
9、已知A、B、C是表面积为![]() 的球面上三点,AB=2,BC=4,∠ABC=60°O为球心,则直线OA与截面ABC所成的角是( )
的球面上三点,AB=2,BC=4,∠ABC=60°O为球心,则直线OA与截面ABC所成的角是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
![]()
10、已知集合A、B、C满足:![]() ,则下列结论中一定正确的是( )
,则下列结论中一定正确的是( )
A、B=C
B、A![]() B= A
B= A![]() C C、 A
C C、 A![]() CUB=
A
CUB=
A![]() CUC D、CUA
CUC D、CUA![]() C= CUA
C= CUA![]() B
B
二、填空题(共20分)
11、若![]()
![]() ,则直线
,则直线![]() 过定点
。
过定点
。
12、已知![]() 。
。
![]()
![]()

![]() 13、如图,
13、如图,![]() y P
y P
![]() 点,点P在椭圆上,
点,点P在椭圆上,![]() 则
F1 O F2 x
则
F1 O F2 x
椭圆的离心率为 。
14、已知在同一平面上,![]() 三向量所成的角均相等,且
三向量所成的角均相等,且![]()
![]()
![]() 则
则![]()
。
15、直角三角形ABC的斜边AB在平面![]() 内,AC和BC与平面
内,AC和BC与平面![]() 所成的角分别为30°和45°,CD是AB边上的高,则CD与
所成的角分别为30°和45°,CD是AB边上的高,则CD与![]() 所成的角为
。
所成的角为
。
三、解答题(12′+13′+13′+14′+14′+14′,共80分)
16、已知![]() 的值.
的值.
17、已知正四面体A—BCD,有一只小虫自顶点A沿每一条棱以等可能的概率爬到另外三个顶点B、C、D,然后又从B、C、D中的一个顶点沿每一条棱以等可能的概率爬到另外三个顶点,依次进行下去。记Pn为第n次到顶点A的概率。
⑴ 求Pn的通项公式;
⑵ 求2006次爬到顶点A的概率.
18、已知函数f(x)=-x3+3x2+9x+a,
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
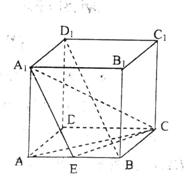 19.如图,在正方体
19.如图,在正方体![]() 中,E为AB的中点。
中,E为AB的中点。
(Ⅰ)求异面直线BD1与CE所成角的余弦值
(Ⅱ)求二面角 A1—EC—A的大小.
20、已知椭圆![]() 的方程为
的方程为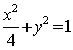 ,双曲线
,双曲线![]() 的左、右焦点分别是
的左、右焦点分别是![]() 的左、右顶点,而
的左、右顶点,而![]() 的左、右顶点分别是
的左、右顶点分别是![]() 的左、右焦点。
的左、右焦点。
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 及双曲线
及双曲线![]() 都恒有两个不同的交点,且
都恒有两个不同的交点,且![]() 与
与![]() 的两个交点,A和B满足
的两个交点,A和B满足![]() (其中O为原点),求
(其中O为原点),求![]() 的范围。
的范围。
21、已知数列![]() 是由正数组成的等差数列,
是由正数组成的等差数列,![]() 是其前
是其前![]() 项的和,并且
项的和,并且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求使不等式![]() 对一切
对一切![]() 均成立的最大实数
均成立的最大实数![]() ;
;
(3)对每一个![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
《参考答案》
一、选择题
CBABA BCADD
二、填空题
11、(![]() ) 12、2 13、
) 12、2 13、![]() 14、49或
14、49或![]() 15、60°
15、60°
三、解答题
16、解:由![]()
![]()
得 ![]() 又
又![]()
于是 ![]()
![]()
17、解:⑴由于第n次到顶点A是从B、C、D三个顶点爬行而来,从其中任何一个顶点
达到A的概率都是![]() ,而第n-1次在顶点A与小虫在顶点B、C、D是对立事件。
,而第n-1次在顶点A与小虫在顶点B、C、D是对立事件。
因此,![]() ,∴
,∴![]()
∴![]()
⑵ P![]() =
=![]() (-
(-![]() )
)![]() +
+![]()
18、解:(I) f ’(x)=-3x2+6x+9.令f ‘(x)<0,解得x<-1或x>3,
所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(II)因为f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,
所以f(2)>f(-2).因为在(-1,3)上f ‘(x)>0,所以f(x)在[-1, 2]上单调递增,
又由于f(x)在[-2,-1]上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]
上的最大值和最小值,于是有 22+a=20,解得 a=-2.
故f(x)=-x3+3x2+9x-2,因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7
19、解(Ⅰ)设正方体的棱长为1,延长DC至G,使CG=
DC,连结BD、![]()
![]() ,∴四边形EBGC是平行四边形.
,∴四边形EBGC是平行四边形.
![]() ∴BG∥EC. ∴
∴BG∥EC. ∴

![]() 在
在
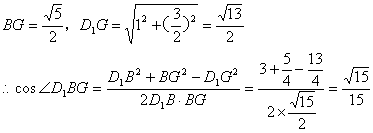 |
![]() 即异面直线 与CE所成角的余弦值是
即异面直线 与CE所成角的余弦值是
![]()
![]()
![]()
![]() (Ⅱ)过 作
交CE的延长线于H.连结AH. ∵ 平面ABCD,∴AH是 在平面ABCD内的射影.∴AB⊥CH.
(Ⅱ)过 作
交CE的延长线于H.连结AH. ∵ 平面ABCD,∴AH是 在平面ABCD内的射影.∴AB⊥CH.
![]()
![]() 则 为二面角
的平面角
则 为二面角
的平面角
底面ABCD如图所示.
由于∠AHE=∠B=90°,∠AEH=∠CEB,则△AHE∽△CBE
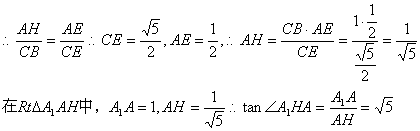 |
![]()
![]() 则二
角的大小为
则二
角的大小为
20、解:(1)设双曲线![]() 的方程为
的方程为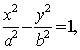 则
则![]()
再由![]() 得
得![]() ,故
,故![]() 的方程为
的方程为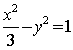
(2)将![]() 代入得
代入得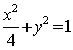 ,得
,得
![]() ,由直线
,由直线![]() 与
与![]() 恒有两个不同的交点,得:
恒有两个不同的交点,得:
![]() ,即
,即![]() ①
①
将![]() 代入
代入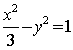 ,得
,得
![]() ,由直线
,由直线![]() 与
与![]() 恒有两个不同的交点,得:
恒有两个不同的交点,得:
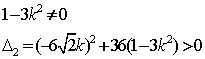
即![]() 且
且![]() ②
②
设![]() ,则
,则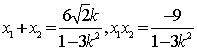
由![]() 得
得![]() ,而
,而
![]()
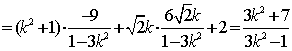 ,
,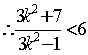
即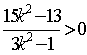 ,解得
,解得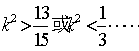 ③
③
由①、②、③得: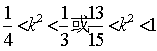
故K的取值范围为: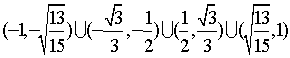 。
。
21、解:(1)设![]() 的公差为
的公差为![]() ,由题意
,由题意![]() ,且
,且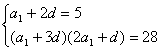
![]() ,
,
数列![]() 的通项公式为
的通项公式为![]()
(2)由题意![]() 对
对![]() 均成立
均成立
记![]()
则![]()
![]() ,
,![]() 随
随![]() 增大而增大
增大而增大
![]() 的最小值为
的最小值为![]()
![]() ,即
,即![]() 的最大值为
的最大值为![]()
(3)![]()
![]() 在数列
在数列![]() 中,
中,![]() 及其前面所有项之和为
及其前面所有项之和为
![]()
![]() ,即
,即![]()
又![]() 在数列
在数列![]() 中的项数为:
中的项数为:![]()
且![]()
所以存在正整数![]() 使得
使得![]()