高三第二次月考数学试题（文科）

高三第二次月考数学试题（文科）

命题人：刘海军　审校人：朱伙昌　总分150分

一．选择题：（本大题共12小题，每小题5分，共60分.在每小题给出的四个选

项中， 只有一项是符合题目要求的）

1．设P、S、T是三个非空的集合，若xÎP是xÎS或xÎT成立的充要条件，则xÎS是xÎP的（　）

A．充分不必要条件　　　　　　　　　　　　　　　　 B．必要不充分条件

C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不要条件

2．下列函数中以p为周期且在（，p）上是增函数的是（　）

A．y=sinx　　　　　 B．y=3cos²x　　　　　　　　C．y=()^cosx 　　　　　　 D．y=cotx

3．DABC中，tanA是第三项为-4,第七项为4的等差数列的公差，tanB是第三项为，第六项为9的等比数列的公比，则DABC是（　）

A．锐角三角形　　 B．直角三角形　　　　　　C．钝角三角形　　　　　　D．等腰三角形

4．已知双曲线（a>0)的一条渐近线与直线2x-y+3=0垂直，则该双曲线的准线方程是（　）

A．x=±　　　　　B．x=±　　　　　　　　 C．x=±　　　　　　　 D．x=±

5．正三棱锥P-ABC侧棱长为a, M、N分别是PC、BC中点，且AM^MN,则P-ABC外接球的面积是（　）

A．36pa² B．9pa² C．6pa² D．3pa²

6．设有编号为1，2，3，4，5的5个茶杯和5个杯盖，将五个杯盖盖在五个茶杯上，则至少有两个杯盖和茶杯的编号相同的盖法有（　）

A．30种　　　　　　　 B．31种　　　　　　　 C．32种　　　　　　　　　　　D．36种

7．将一颗骰子连掷三次，至少出现一次1点向上的概率是（　）

A．　　　　　　　　　　 B．　　　　　　　 C．　　　　　　　　　　　　　　D．

8．已知x>0, y>0，且，则xy有（　）

A．最大值24　　　　B．最小值24　　　　C．最大值2　　　　　D．最小值2

9．已知平面直角坐标中，直线的方向向量为=（-4，3）,点O（0，0），A（1，-2）在上的射影分别为O'、A'，且，则l等于（　）

A．　　　　　　　　　B．-　　　　　　　　 C．2　　　　　　　　　　　　　　D．-2

10．函数f(x)=Asin(wx+j)(A¹0, w>0，j<)的图象关于直线x=对称，且周期为p，则（　 ）

A．f(x)最大值为A　　　　　　　　　　　　　　　　　 B．f(x)图象过点（0，）

C．f(x)图象关于点（，0）对称　　　　 D．f(x)在[，]上递减

11．已知y=f(x)在R上的单调函数,且函数y=f(x+1)图象与y=f ^-1(x-2)图象关于直线y=x对称，又f(1)=1，则f(1004)的值为（　）

A．2005　　　　　　　 B．2006　　　　　　　　C．2007　　　　　　　　　　　D．2008

12．已知函数f(x)对定义域中的任意两个值x₁, x₂（x₁¹x₂）都有f(x₁)+f(x₂)>2f()下列函数①y=x²-x　②y=()^x ③y= -log₂(-x) ④y=tanx中可以为函数f(x)的是（　）

A．①③　　　　　　　 B．②④　　　　　　　　C．①④　　　　　　　　　　　D．②③

二．填空题（4´4=16分）

13．(x³+)¹⁰展开式中不含x的项是__________

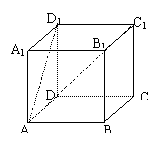
14．如图,长方体ABCD-A₁B₁C₁D₁，ÐDAD₁=45⁰，

ÐCDC₁=30⁰，那么异面直线AD₁与DC₁所成角的余弦值

是___________。

15．抛物线y=x²上点A处的切线到直线3x-y+1=0的角为45⁰，则点A的坐标为________

16．已知关于x的方程x²+(2a+b)x+b+1=0两实根为a、b,且aÎ(-1,1), bÎ（1，2）,则a²+b²取值范围是_________

三．解答题（74分）

17．（本题12分）已知向量=(sinx, cos2x)，=(4sin²（+), 1) (<x<p)，若·=,求cos(2x+)的值。

18．（本题12分）已知数列{a_n}是首项a₁>0，公比q>0的等比数列，设b_n＝log₂a_n，且b₁+b₂+b₃=6, b₁·b₂·b₃=0，数列{b_n}的前n项和为Ｓ_n。

（１）求数列{b_n}的通项。

（２）设f(n)＝…＋,当f(n)最大时，求n的值。

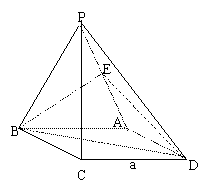19．（本题12分）四棱锥P-ABCD中，底面ABCD是以ÐABC为60⁰的菱形，PC^平面ABCD，且PC=CD=a, E是PA的中点。

（1）求证：平面EBD^平面ABCD。

（2）求点E到平面PBC的距离。

（3）求二面角A-BE-D的正切值。

20．（本题12分）甲、乙两人进行乒乓球比赛且它们的水平相当，比赛用“七局四胜制”，若已知甲先胜了前两局，求：

（1）乙获胜的概率。

（2）比赛打满七局的概率。

21．（本题12分）已知f(x)=ax³+bx²+cx+d（a¹0)是R上的奇函数，且x=1时f(x)取极值-2，g(x)=f(x)-mx²

（1）求f(x)的解析式。

（2）若g(x)是[1，2]上的单调函数，求实数m的取值范围。

22．（本题14分）已知椭圆c: (a>b>0, bÎN*)与直线6x-5y-28=0交于不同两点M、N，B是椭圆的短轴上端点，F为右焦点，且有,

(1)求椭圆c的方程。

(2)设椭圆C的左焦点为F'，问椭圆上是否存在一点P使与的夹角为60⁰？证明你的结论。

第二次月考数学答案(文）

一．选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

题号	1	2	3	4	5	6	7	8	9	10	11	12
选项	A	B	A	D	D	B	C	B	B	C	C	A

二．填空题：本大题共4小题，每小题4分，共16分。

13．252　　　　　　 14． 15．（ ，）　　 16．[，10）

三．解答题

17．解：∵·=4sinxsin²(+)+cos2x…………2分

=2sinx(1+sinx)+cos2x

=2sinx+2sin²x+1-2sin²x

=2sinx+1…………………………………………6分

∴sinx=,又∵xÎ(, p)　∴ cosx= -

∴cos(2x+)=cos2x-sin2x………………8分

=………………12分

18.解：∵{a_n}是等比数列Þ{b_n}为等差数列………………2分

由b₁+b₂+b₃=6Þb₂=2

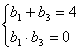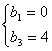∴解得 或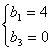…………4分

从而得b_n=2(n-1),或b_n=6-2n……………………6分

（2）若b_n=2(n-1）时

则S_n=n(n-1)　∴f (n)=无最大值……8分

若b_n=6-2n时

则S_n=5n-n² ∴f(n)= -n²+n= -(n-)²+

∴n=4或n=5时，f(n)最大。

综合上述，f(n)最大时，n=4或5……………………12分

19．解（1）连AC、BD交于O，连OE，∵E为PA中点，则OE//PC

∵PC^DABCD, ∴OE^平面ABCD

OEÌ面EBD，∴平面EBD^平面ABCD…………4分

（2）过O作OM^BC于点M

∵PC^面ABCD，OM^平面ABC

又∵OE//PC，∴OE//平面PBC

∴E到平面PBC的距离即为OM的长。

OM=Obsin30⁰=a

∴E到平面PBC距离为a…………8分

（3）过O作ON^BE于N，连AN。

可证：ÐANO为二面角A-BE-D的平面角…………10分。

计算理tanÐANO=

∴二面角A-BE-D的正切值为………………12分

20．解（1）P=()⁴+C₄³·()⁴·()=

(2)P= C₄¹·()⁴·()+C₄³·()⁴·()==

21．（1）∵f(x)为奇函数

∴f(-x)= -f(x)Þb=d=0……………………2分

∴f(x)=ax³+cx

又∵f(x)在x=1处取极值-2

∴Þa=1, c= -3

∴f(x)=x³-3x……………………6分

（2）∵g(x)=x³-mx²-3x

∴g '(x)=3x²-2mx-3

由g(x)是[1，2]上的单调函数

1）若g(x)在[1, 2]上递增，则g '(x)³0恒成立Þm£0…………8分

2）若g(x)在[1，2]上递减，则g '(x)£0Þm³………………10分

∴mÎ(-¥, 0]È[ ,+¥)……………………………………12分

22．（1）B(0, b)，F(c, 0）,其中c=, 设M(x₁, y₁), N(x₂, y₂)

∵Þx₁+x₂=3c, y₁+y₂=-b…………①

……③

……②

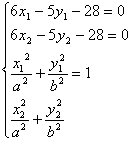又∵Þ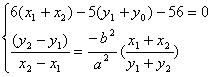

由①②③Þ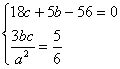

又a²=b²+c²　 , bÎN*

解得：a=2, b=4

∴椭圆C：

(2)不存在，假设存在点P(x₀, y₀)，使与夹角为60⁰

∵F(-2, 0)，F（2，0）, 离心率e=

∴PF'=a+ex₀　PF=a-ex₀

由FF'² =PF'²+PF²-2PF' ·PFcosÐF'PF

Þa²+3e²x₀²=4c²

Þx₀²= -4 无解

∴P不存在。