高三第三次月考数学(理)试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,满分150分,考试时间120分钟。
第I卷(选择题,共40分)
一.选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、已知集合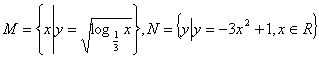 ,则
,则![]() =
=
A、φ B、![]() C、
C、![]() D、
D、![]()
2、等差数列{an}的前n项和为Sn,若S6-S2=4,则S8的值是
A、6 B、4 C、2 D、8
3、函数![]() 是
是
A、非奇非偶函数 B、仅有最小值的偶函数
C、仅有最大值的偶函数 D、既有最大值又有最小值的偶函数
4、![]() 为增函数的区间是
为增函数的区间是
A ![]() B
B
![]() C
C ![]() D
D ![]()
5、二次函数y=f(x)的图象过原点,且它的导数y=f’(x)的图象是过第一、二、三象限的一条直线,则函数y=f(x)的图象的顶点在
A、第一象限 B、第二象限 C、第三象限 D、第四象限
6、设函数f定义如下表,数列{xn}满足x0=3,且对任意的自然数n均有xn+1=f(xn),则x2007=
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(x) | 6 | 7 | 4 | 5 | 1 | 2 | 3 |
A、3 B、2 C、6 D、7
7、已知二次函数y=n(n+1)x2-(2n+1)x+1,当n依次取1,2,3,4,…,k时,其图象在x轴上截得的线段长度的总和为
A.1 B.![]() C.
C.
![]() D.
D.
![]()
8、某林厂年初有森林木材存量S m3,木材以每年25%的增长率生长,而每年末要砍伐固定的木材量x m3,为实现经过两次砍伐后的木材的存量增加50%,则x的值是
A. ![]() B.
B.![]() C.
C.
![]() D.
D.![]()
一、选择题答题卡(每小题5分,共40分)
请把第一卷的答案序号填写在下表
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | D | D | C | C | B | B | A |
全卷得分表
| 题号 | 一 | 二 | 三 | 全卷 总分 | |||||
| 9~14 | 15 | 16 | 17 | 18 | 19 | 20 | |||
| 得分 | |||||||||
第II卷(非选择题 共110分)
二.填空题(本大题共6小题,每小题5分,共30分.把答案填在题中横线上.)
9、已知向量![]() ,则实数m的值是
,则实数m的值是 ![]() ;
;
10、公差不为0的等差数列第二、三、六项成等比数列,则公比等于 3 .;
11、曲线xy=1与直线y=x、y= -3所围成的平面图形的面积是 4-ln3 ;
12、用二分法研究方程x3+3x-1=0的一个近似解x=x0问题。(1)若借助计算器,算得:
第一次:f(0)<0,f(0.5)>0![]() x0∈ (0,0.5)
;
x0∈ (0,0.5)
;
第二次: f(0.25)<0, f(0.5)>0 ![]() x0∈(0,0.25)
;
x0∈(0,0.25)
;
第三次:f(0.25)<0,f(0.375)>0![]() x0∈(0.25,0.375)
x0∈(0.25,0.375)
第四次:f(0.3125)<0,f(0.375)>0![]() x0∈(0.3125,0.375)
x0∈(0.3125,0.375)
第五次:f(0.31225)<0,f(0.34375)>0![]() x0∈(0.3125,0.34375)
x0∈(0.3125,0.34375)
第六次:f(0.3125)<0,f(0.)>0![]() x0∈(0.3125,0.)
x0∈(0.3125,0.)
……
(2)若误差不超过0.1,必须算 4 次,近似解x0= 0.34375 .
13、14在以下三题中选二道。
1、函数![]() 的最大值是 13 ;
的最大值是 13 ;
2、△ABC底边BC=10,![]() ,以B为极点,BC为极轴,则顶点A的轨迹方程是
,以B为极点,BC为极轴,则顶点A的轨迹方程是
p=20cosθ-10 ;
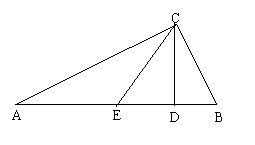 3、如图,CD是Rt△ABC斜边AB上的高,将△ABC沿CD折叠,B点恰好落在AB的中点E处,则
3、如图,CD是Rt△ABC斜边AB上的高,将△ABC沿CD折叠,B点恰好落在AB的中点E处,则![]() = 30° 。
= 30° 。
三.解答题(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤)
15、(本小题满分12分)
已知sin(![]() -x)=
-x)=![]() ,
, ![]() <x<
<x<![]() ,求
,求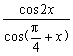 的值.
的值.
解:∵(![]() -x)+(
-x)+(![]() +x)=
+x)=![]() ,
,![]() <x<
<x<![]()
∴cos(![]() +x)=sin(
+x)=sin(![]() -x). cos(
-x). cos(![]() -x)=
-x)=![]() 4分
4分
又cos2x=sin(![]() -2x)
-2x)
=sin2(![]() -x)=2sin(
-x)=2sin(![]() -x)cos(
-x)cos(![]() -x),
-x),
∴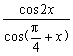 =2cos(
=2cos(![]() -x)=2×
-x)=2×![]() =
=![]() 12分
12分
16、(本小题满分12分)
设f(x)=x3-![]() -2x+5.
-2x+5.
(1)求f(x)的单调区间;
(2)当x∈[1,2]时,f(x)<m恒成立,求实数m的取值范围.
解:(1)![]() (x)=3x2-x-2=0,得x=1,-
(x)=3x2-x-2=0,得x=1,-![]() .在(-∞,-
.在(-∞,-![]() )和[1,+∞]上
)和[1,+∞]上![]() (x)>0,f(x)为增函数;在[-
(x)>0,f(x)为增函数;在[-![]() ,1]上
,1]上![]() (x)<0,f(x)为减函数.所以所求f(x)的单调增区间为(-∞,-
(x)<0,f(x)为减函数.所以所求f(x)的单调增区间为(-∞,-![]() )和[1,+∞],单调减区间为[-
)和[1,+∞],单调减区间为[-![]() ,1]. 6分
,1]. 6分
(2)当x∈[1,2]时,显然![]() (x)>0,f(x)为增函数,f(x)≤f(2)=7.
(x)>0,f(x)为增函数,f(x)≤f(2)=7.
∴m>7. 12分
17、(本小题满分14分)
在等差数列![]() 中,首项
中,首项![]() ,数列
,数列![]() 满足
满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)求![]()
解(1)设等差数列![]() 的公差为d,
的公差为d, ![]() ,
,
![]()
由![]() ,解得d=1.
5分
,解得d=1.
5分
![]() 7分
7分
(2)由(1)得![]()
设![]() ,
,
则![]() 9分
9分
两式相减得![]() 11分
11分
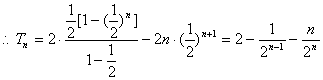 14分
14分
18、(本题满分14分)
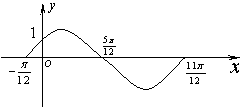
函数f1(x)=A sin (w x+ j ) (A>0, w >0, j < )的一段图象过点![]() ,如图所示.
,如图所示.
(1)求函数f1 (x)的解析式;
 (2)将函数y= f1 (x)的图象按向量a = ( , 0)平移,得到函数 y =
f2 (x),求y=
f1 (x)+ f2 (x)的最大值,并求此时自变量
(2)将函数y= f1 (x)的图象按向量a = ( , 0)平移,得到函数 y =
f2 (x),求y=
f1 (x)+ f2 (x)的最大值,并求此时自变量![]() 的集合.
的集合.
解:⑴ 由图知: T = ―(―) = p,于是 w = = 2 2分
设f1(x)=A sin (2x+j )
将函数f (x)=A sin 2x的图象向左平移![]() ,得f1(x)=A
sin (2x+j )的图象,
,得f1(x)=A
sin (2x+j )的图象,
则![]() ,∴ f1(x)=A sin (2x+ ), 4分
,∴ f1(x)=A sin (2x+ ), 4分
将(0,1)代入f1(x)=A sin (2x+ ), 易得A=2 7分
故 f1(x) = 2 sin (2x+ ) 8分
⑵ 依题意:![]() 10分
10分
∴ ![]()
![]() 12分
12分
当![]() ,即
,即![]() 时,
时,![]()
此时,![]() 的取值集合为
的取值集合为![]() 14分
14分
19、(本小题满分14分)已知函数![]()
(1)若f(x)的图象有与x轴平行的直线,求b的取值范围;
(2)若f(x)在x=1处取得极值,且x∈(-1,2),f(x)<c2恒成立,求c的取值范围。
解:(1)f(x)=x3+ax2+bx+c,f¢(x)=3x2-x+b
由f¢(x)=0有实数解,所以![]()
故b≤1/12
(2)x=1 f¢(x)=0的一根,可求得x=-![]() 是另一根,f(x)=
是另一根,f(x)=![]() +c
+c
为极大值,而f(2)=2+c,则f(2)=2+c为最大值。
要使f(x)<c2(xÎ(-1,2))恒成立,只需c2≥f(2)=2+c
解得c≤-1或c≥2
20、(14分)已知定义域为R的二次函数![]() 的最小值为0且有
的最小值为0且有![]() ,直线
,直线![]() 被
被![]() 的图像截得的弦长为
的图像截得的弦长为![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)求函数![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求数列
,求数列![]() 的最值及相应的n。
的最值及相应的n。
(1)解:设![]() ,则直线
,则直线![]() 与
与![]() 图象的两个交点为(1,0),
图象的两个交点为(1,0),
![]() ………………………2分
………………………2分
![]()
![]() …………………4分
…………………4分
(2)![]()
![]()
![]()
![]() …………6分
…………6分
![]() 数列
数列![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列…………8分
的等比数列…………8分
![]() …………9分
…………9分
(3)![]()
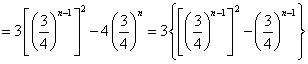 令
令 ![]() …………10分
…………10分
则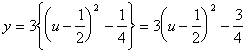
![]() ,
,![]() 的值分别为
的值分别为![]() ……,经比较
……,经比较![]() 距
距![]() 最近…………12分
最近…………12分
∴当![]() 时,
时,![]() 有最小值是
有最小值是![]() ,
………………………………13分
,
………………………………13分
当![]() 时,
时,![]() 有最大值是0。
…………………………………14分
有最大值是0。
…………………………………14分