高三第九次考试数学试题(理科)
一、选择题(每小题5分,10小题,共50分)
1、定义集合M与N的新运算,M+N=![]() 或
或![]() 且
且![]() ,则(M+N)+N等于( )
,则(M+N)+N等于( )
A、![]() B、
B、![]() C、M D、N
C、M D、N
2、已知![]() ,且ab<0,则
,且ab<0,则![]() 是复数
是复数![]() 为纯虚数的( )
为纯虚数的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
3、已知曲线![]() 与函数
与函数![]() 和
和![]() 分别交于
分别交于![]() ,
,![]() 两点,则
两点,则![]() 的值为( )
的值为( )
A、1 B、2 C、![]() D、3
D、3
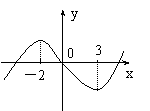 4、函数
4、函数![]() 图象如右图,则函数
图象如右图,则函数![]() 的单调递增区间为( )
的单调递增区间为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、已知函数![]() 的最大值为2,则
的最大值为2,则![]() 的最小正周期为( )
的最小正周期为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,有下列四个命题:
,有下列四个命题:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]()
其中正确命题是:( )
A、①② B、③④ C、②④ D、①③
7、已知0为直角坐标系原点,P、Q的坐标满足不等式组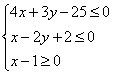 ,则
,则![]() 的最小值为( )
的最小值为( )
A、![]() B、
B、![]() C、
C、![]() D、0
D、0
8、湖南师大数学教育专业6名青年志愿者,为响应团中央发起的中国青年志愿者扶贫活动计划,志愿到湘西自治州的永顺、古丈、凤凰三地任教五年,则一县4名,另两县每县一名的概率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、过正三棱锥S-ABC的侧棱SB和底面ABC的中心O作截面SBO,已知截面是等腰三角形,则侧面与底面所成角的余弦值为( )
A、![]() B、
B、![]() C、
C、![]() 或
或![]() D、
D、![]() 或
或![]()
10、设![]()
![]() 表示a,b,c中的最小值),则y的最大值为( )
表示a,b,c中的最小值),则y的最大值为( )
A、2 B、3 C、4 D、5
二、填空题(每小题5分,5小题,共25分)
11、在![]() 的展开式中,
的展开式中,![]() 的系数为
(用数字作答)。
的系数为
(用数字作答)。
12、椭圆![]() 的左、右焦点分别为F1,F2,若线段F1F2恰好被两抛物线
的左、右焦点分别为F1,F2,若线段F1F2恰好被两抛物线![]() 的焦点及顶点四等分,则椭圆的离心率为
。
的焦点及顶点四等分,则椭圆的离心率为
。
13、设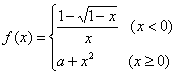 ,要使函数
,要使函数![]() 在
在![]() 内连续,则a的值为
。
内连续,则a的值为
。
14、由一个数列中部分项按原来次序排列的数列叫做这个数列的子数列,试在无穷等比数列![]() 中找出一个无穷等比的子数列,使它们所有项和为
中找出一个无穷等比的子数列,使它们所有项和为![]() ,这个数列的通项公式为
。
,这个数列的通项公式为
。
15、下列四个命题:是否需要在“ ”处添加一个条件才能构成真命题?如需要,请填写这个条件,如不需要,请把“ ”用“/”划掉(全部正确得5分,漏一个或错一个得0分)
![]()
![]() ①
①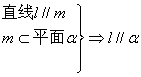 ; ②
; ②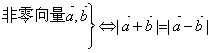 ;
;
![]() ③
③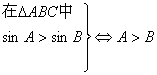 ;
;
![]() ④
④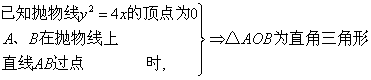
 三、解答题(本大题有6道小题,满分75分)
三、解答题(本大题有6道小题,满分75分)
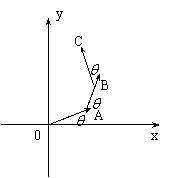
16、(本题满分12分)如图,从原点O引向量![]() ,使其与
,使其与
x轴的夹角为![]() ,从它的终点引向量
,从它的终点引向量![]() ,使其与
,使其与![]() 的夹角为
的夹角为
![]() ,同样引向量
,同样引向量![]() ,使其与
,使其与![]()
夹角为![]() ,设
,设![]()
(1)用a及![]() 表示C点的坐标;
表示C点的坐标;
(2)若点C落在y轴上,求此时![]() 的值(
的值(![]() )
)
17、(本题满分12分)一台仪器每启动一次都随机地出现一个5位的二进制数A=![]() ,其中A的各数位中,
,其中A的各数位中,![]() ,
,![]() 出现0概率为
出现0概率为![]() ,出现1的概率为
,出现1的概率为![]() ,例如A=10011,其中
,例如A=10011,其中![]() ,
,![]() ,设
,设![]() ,当启动仪器一次时,求:
,当启动仪器一次时,求:
(1)![]() 的概率。
的概率。
(2)![]() 的数学期望。
的数学期望。
18、将如图(1)的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结部分线段后围成一个空间几何体,如图(2)所示
(1)求异面直线BD与EF所成的角大小。
(2)求二面角D-BF-E的大小。
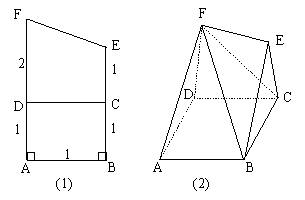 (3)求证:A、B、C、D、F这五个点在同一球面上,并求该球的表面积。
(3)求证:A、B、C、D、F这五个点在同一球面上,并求该球的表面积。
19、(本题满分12分)已知函数![]()
(1)若![]() ,求
,求![]() 的极值;
的极值;
(2)若![]() 在定义域内单调递减,求实数k的取值范围。
在定义域内单调递减,求实数k的取值范围。
20、(本题满分13分)已知数列![]() 中,
中,![]() ,且
,且![]() 是函数
是函数![]() 的一个极值点。
的一个极值点。
(1)求数列![]() 的通项公式;
的通项公式;
(2)若点Pn的坐标为![]() ,过函数
,过函数![]() 图象上的点
图象上的点![]() 的切线始终与
的切线始终与![]() 平行(点O为坐标原点);求证:当
平行(点O为坐标原点);求证:当![]() 时,不等式
时,不等式![]() 对
对![]() 成立。
成立。
21、(本题满分14分)如图所示,O是线段AB的中点,AB=2c,以点A为圆心,2a为半径作一圆,其中![]() 。
。
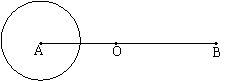
(1)若圆A外的动点P到B的距离等于它到圆周的最短距离,建立适当坐标系,求动点P的轨迹方程,并说明轨迹是何种曲线;
(2)经过点O的直线l与直线AB成60°角,当c=2,a=1时,动点P的轨迹记为E,设过点B的直线m交曲线E于M、N两点,且点M在直线AB的上方,求点M到直线l的距离d的取值范围。
参 考 答 案
1、C 2、C 3、D 4、D 5、C 6、D 7、A 8、B 9、C 10、A
11、-14 12、![]() 13、
13、![]() 14、
14、![]()
15、①![]() ②
②![]() (或
(或![]() 与
与![]() 垂直) ③/ ④(4,0)
垂直) ③/ ④(4,0)
16、解:(1)![]() (6分)
(6分)
(2)由已知![]()
即![]()
∴![]()
∵![]() ,∴
,∴![]() ∴
∴![]() (12分)
(12分)
17、解:(1)∵![]() ,∴
,∴![]() 表示
表示![]() 中出现2个1,2个0。
中出现2个1,2个0。
∴![]() (4分)
(4分)
(2)![]() 的可能取值1,2,3,4,5
的可能取值1,2,3,4,5
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (9分)
(9分)
![]() (12分)
(12分)
18、解:(1)60° (4分)
(2)90° (8分)
(3)易知BF中点H为球心。
即HA=HB=HC=HD=HF=![]()
∴![]() (12分)
(12分)
19、解:(1)![]()
由![]() 又
又![]() 定义域为
定义域为![]()
∴![]() 时,
时,![]() ,即
,即![]() 在
在![]() 时,
时,![]() ,即
,即![]() 在
在![]() ,∴
,∴![]() 极大值为
极大值为![]() (6分)
(6分)
(2)![]() ,定义域为(0,+
,定义域为(0,+![]() ),
),
且![]() 在(0,+
在(0,+![]() ),上恒成立。
),上恒成立。
记![]() ,则
,则![]() ,由
,由![]() ,得x=e(8分)
,得x=e(8分)
∴当![]() 时,
时,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() 为减函数。
为减函数。
∴当x=e时,![]() 取得最大值
取得最大值![]() 。
。
为使![]() 在(0,+
在(0,+![]() )上恒成立,则
)上恒成立,则![]() 恒成立,
恒成立,
∴![]() ,当
,当![]() 时,只有一点x=e使得
时,只有一点x=e使得![]() ,不影响
,不影响![]() 的单调性,
的单调性,
∴![]() (12分)
(12分)
20、解:(1)![]()
∴![]()
∴![]()
∴![]() ,…
,…![]()
∴![]() ,∴
,∴![]() (4分)
(4分)
![]() 时,
时,![]()
∴![]()
综上 ![]() (5分)
(5分)
(2)由![]() 得
得![]()
∴![]() ∵
∵![]() ,
,
∴![]()
∴![]()
![]()
21、解:(1)以直线AB为x轴,线段AB的垂直平分线为y轴建立直角坐标系,则A(-c,0),B(c,0)
依题意:![]()
∴点P的轨迹为以A、B为焦点,实半轴为a,虚半轴为![]() 的双曲线右支
的双曲线右支
∴轨迹方程为:![]() 。(6分)
。(6分)
(2)法一:设M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() )
)
依题意知曲线E的方程为
![]() ,l的方程为
,l的方程为![]() (7分)
(7分)
设直线m的方程为![]()
由方程组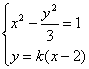 ,消去y得
,消去y得
![]() ①
①
∴![]() (9分)
(9分)
∵直线![]() 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点
∴![]() 及
及![]() ,从而
,从而![]() (10分)
(10分)
由①得![]()
解得![]() 且
且![]()
当x=2时,直线m垂直于x轴,符合条件,∴![]() (11分)
(11分)
又设M到l的距离为d,则![]()
∵![]()
∴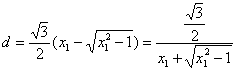
设![]() ,
,![]() (12分)
(12分)
由于函数![]() 与
与![]() 均为区间
均为区间![]() 的增函数
的增函数
∴![]() 在
在![]() 单调递减
单调递减
∴![]() 的最大值=
的最大值=![]() (13分)
(13分)
又∵![]()
而M的横坐标![]() ,∴
,∴![]() (14分)
(14分)
法二:![]() 为一条渐近线
为一条渐近线
①m位于![]() 时,m在无穷远,此时
时,m在无穷远,此时![]() (9分)
(9分)
②m位于![]() 时,
时,![]() ,d较大
,d较大
由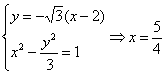 (12分)
(12分)
点M![]()
∴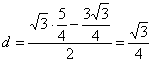 (14分)
(14分)
故 ![]()