高三第三次月考数学试题(理科)
总分150分
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的4个选项中,只有一项是符合题目要求的)
1.
设全集U=R,![]() ,则
,则![]() =(
)
=(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 已知复数![]() 满足
满足![]() ,那么复数
,那么复数![]() 的虚部为( )
的虚部为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 设a,b∈R则“lg (a2+1)<lg (b2+1)”是a<b的
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
4.
函数![]() 的反函数是( )
的反函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.
过点![]() 作圆
作圆![]() 的两切线,设两切点为
的两切线,设两切点为![]() 、
、![]() ,圆心为
,圆心为![]() ,则过
,则过![]() 、
、![]() 、
、![]() 的圆方程是 ( )
的圆方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6. 直线![]() 的方向向量为
的方向向量为![]() ,直线
,直线![]() 的倾角为
的倾角为![]() ,则
,则![]() ( )
( )
A.
![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
7.
设O是△ABC内部一点,且![]() ,则△AOB与△AOC的面积之比为
,则△AOB与△AOC的面积之比为
A.2
B.![]() C.1
D.
C.1
D.![]()
8. 已知关于x的方程:![]() 在区间(3,4)内有解,则实数a的取值范围是( )
在区间(3,4)内有解,则实数a的取值范围是( )
A.![]() B.
B.![]() ) C.
) C.![]() D.
D.![]()
9. 在等差数列![]() 中,若
中,若![]() ,则
,则![]() 的值为( )
的值为( )
A.14 B.15 C.16 D.17
10. 函数f(x)=(3sinx-4cosx)·cosx的最大值为( )
A.5 B.![]() C.
C.![]() D.
D.![]()
11.
平面向量也叫二维向量,二维向量的坐标表示及其运算可以推广到n(n≥3)维向量,n维向量可用(x1,x2,x3,x4,…,xn)表示.设a=(a1, a2, a3, a4,…, an),b=(b1, b2,
b3, b4,…,bn),规定向量a与b夹角θ的余弦为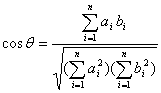 .
.
当a=(1, 1,1,1…,1),b=(-1, -1, 1, 1,…,1)时,cosθ= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.
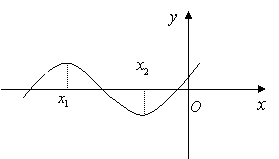
已知函数![]() 的图像如图所示,则下列判断正确的是( )
的图像如图所示,则下列判断正确的是( )
 A.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
一.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)
13.![]() =_________。
=_________。
14.把函数![]() 的图象沿向量
的图象沿向量![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 可以是__________。
可以是__________。
15.若正数![]() 满足
满足![]() ,则
,则![]() 的取值范围是__________。
的取值范围是__________。
16.设函数![]() 的定义域为
的定义域为![]() ,若存在常数
,若存在常数![]() ,使
,使![]() ≤
≤![]() 对一切实数
对一切实数![]() 均成立,则称
均成立,则称![]() 为
为![]() 函数。给出下列函数:
函数。给出下列函数:
①![]() ;②
;②![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() ;
;
⑤![]() 是R上的奇函数,且满足对一切实数
是R上的奇函数,且满足对一切实数![]() 、
、![]() 均有
均有![]() .
.
其中是![]() 函数的序号为 。
函数的序号为 。
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.
(本小题满分12分)已知函数![]()
(Ⅰ)求![]() 的单调增区间;
的单调增区间;
(Ⅱ)在直角坐标系中画出函数![]() 在区间
在区间![]() 上的图象。
上的图象。
18. (本小题满分12分)某小组中有男生、女生若干人,如果从中选一从参加某项测试,女生被选中的概率是![]() ;如果从中选两人参加测试,两人都是女生的概率为
;如果从中选两人参加测试,两人都是女生的概率为![]() (每个人被选中是等可能的).
(每个人被选中是等可能的).
(Ⅰ)求该小组男生、女生各多少人?
(Ⅱ)从该小组中选出3人,求男、女生都有的概率;
(Ⅲ)若对该小组的同学进行某项测试,其中女生通过的概率为![]() ,男生通过的概率为
,男生通过的概率为![]() ,现对该小组中男生甲、乙和女生丙三人进行测试,记通过人数为ξ,求ξ的数学期望.
,现对该小组中男生甲、乙和女生丙三人进行测试,记通过人数为ξ,求ξ的数学期望.
19 .(本小题满分12分)解关于![]() 的不等式
的不等式![]() 。
。
20.(本小题满分12分)已知圆C:![]()
![]() 经过点
经过点![]() 及点
及点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,直线
,直线![]() 与圆C相切。
与圆C相切。
(1)求实数![]() ;
;
(2)若实数![]() 满足约束条件
满足约束条件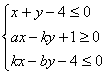 ,且使目标函数
,且使目标函数![]() 取最小值的最优解有无穷多个,求实数
取最小值的最优解有无穷多个,求实数![]() 的值。
的值。
21.(本小题满分12分)已知函数![]() 经过点
经过点![]() ,且在
,且在![]() 时取得极大值0。
时取得极大值0。
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若存在区间![]() 使函数
使函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,求实数
,求实数![]() 的最小值及此时的区间
的最小值及此时的区间![]() 。
。
22.(本小题满分14分)已知数列![]() 中,
中,![]() 且
且![]() 是函数
是函数![]() 的一个极值点。
的一个极值点。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若点![]() 的坐标为
的坐标为![]()
![]() ,过函数
,过函数![]() 图像上的点
图像上的点![]() 的切线始终与
的切线始终与![]() 平行(点O为坐标原点);求证:当
平行(点O为坐标原点);求证:当![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 都成立。
都成立。
第三次月考试题(理科)参考答案
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | D | B | A | C | B | C | C | B | D | D |
二.填空题:(13)-3、(14)![]() 、(15)
、(15)![]() 、(15)、(16)①②④⑤
、(15)、(16)①②④⑤
三.解答题:
17解:(Ⅰ)
![]()
![]()
![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]()
(Ⅱ)图象(略)
18解:(Ⅰ)女生6人,男生4人;…………3分
(Ⅱ)![]() ;………………7分
;………………7分
(Ⅲ)![]() ,
,![]() ,
,
![]() ,
,![]()
![]() .…12分
.…12分
19解:原不等式等价于:![]() ,
,
(1)
当![]() 时,解集为
时,解集为![]() ;
;
(2)
当![]() 时,不等式等价于
时,不等式等价于![]() ,
,
①![]() 时,解集为
时,解集为![]() ;
;
②![]() 时,解集为
时,解集为![]() 。
。
20解:(1)由条件得到,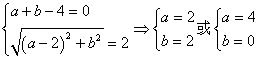 (舍去),
(舍去),
 又因为相切得到:
又因为相切得到: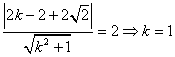 ;
;
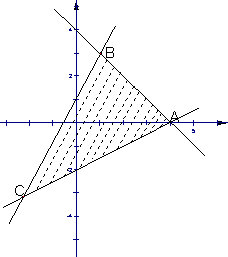
(2)约束条件是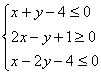 ,得到如图可行域:
,得到如图可行域:
由目标函数![]() 中
中![]() 的几何意义是直线
的几何意义是直线![]() 在
在![]() 轴上的截距,知道当这条直线平行图中BC时,满足条件,所以
轴上的截距,知道当这条直线平行图中BC时,满足条件,所以
![]() 。
。
21解:(Ⅰ)![]() ,依题意得:
,依题意得:
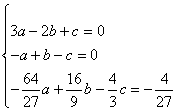 ,解得:
,解得:![]() ,所以:
,所以:![]() ;…4分
;…4分
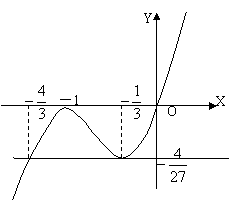 (Ⅱ)由
(Ⅱ)由![]() 得:
得:![]() ,
,
且![]() ,所以
,所以![]() 的大致图像如右图:…6 分
的大致图像如右图:…6 分
①![]() 时:
时:![]() ,
,
所以![]() ;
;
②![]() 时,
时,![]() ,
,
所以![]() ;
;
③![]() 时,
时,![]() ,
,
所以![]() 。
。
综上,实数![]() 的最小值为
的最小值为![]() ,取最小值时,
,取最小值时,![]() ,区间为
,区间为![]() 。……12分
。……12分
22解:(Ⅰ)由![]() 得
得![]() ,
,
![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列。
的等比数列。
![]() 即
即![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,
,
由![]() 时,
时,![]() ,
,
综上可知:![]() 。…………5分
。…………5分
(Ⅱ)由![]() 得到:
得到:![]() ,
,
![]() ,
,
![]()
=![]() …………12分
…………12分