高三第三次月考数学试题(文科)
总分150分
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的4个选项中,只有一项是符合题目要求的)
1.
设全集U=R,![]() ,则
,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.
![]() 的值为
的值为
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
3. 设a,b∈R则“lg (a2+1)<lg (b2+1)”是a<b的
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
4.
函数![]() 的反函数是
的反函数是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.
过点![]() 作圆
作圆![]() 的两切线,设两切点为
的两切线,设两切点为![]() 、
、![]() ,圆心为
,圆心为![]() ,则过
,则过![]() 、
、![]() 、
、![]() 的圆方程是
的圆方程是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.
直线![]() 的方向向量为
的方向向量为![]() ,直线
,直线![]() 的倾角为
的倾角为![]() ,则
,则![]()
A.
![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
7.
设O是△ABC内部一点,且![]() ,则△AOB与△AOC的面积之比为
,则△AOB与△AOC的面积之比为
A.2
B.![]() C.1
D.
C.1
D.![]()
8. 已知关于x的方程:![]() 在区间(3,4)内有解,则实数a的取值范围是
在区间(3,4)内有解,则实数a的取值范围是
A.![]() B.
B.![]() ) C.
) C.![]() D.
D.![]()
9. 在等差数列![]() 中,若
中,若![]() ,则
,则![]() 的值为
的值为
A.14 B.15 C.16 D.17
10. 函数f(x)=(3sinx-4cosx)·cosx的最大值为
A.5 B.![]() C.
C.![]() D.
D.![]()
11. ![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() 是共起点的向量,
是共起点的向量,![]() 、
、![]() 不共线,
不共线,![]() ,则
,则![]() 、
、![]() 、
、![]() 的终点共线的充分必要条件是
的终点共线的充分必要条件是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12. 已知函数![]() 的图像如图所示,则下列判断正确的是
的图像如图所示,则下列判断正确的是
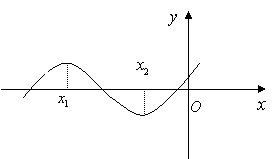 A.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
一.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)
13. 圆![]() 在点
在点![]() 处的切线方程为
处的切线方程为
14.把函数![]() 的图象沿向量
的图象沿向量![]() 平移后得到函数
平移后得到函数![]() 的图象,则向量
的图象,则向量![]() 可以是__________。
可以是__________。
14.若正数![]() 满足
满足![]() ,则
,则![]() 的取值范围是__________。
的取值范围是__________。
16.假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第8行第18列的数开始向右读,请你依次写出最先检测的5袋牛奶的编号 ____________________________________ .(下面摘取了一随机数表的第7行至第9行)
……
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 62 58 79
73 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
……
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知函数![]()
(Ⅰ)求![]() 的单调增区间;
的单调增区间;
(Ⅱ)在直角坐标系中画出函数![]() 在区间
在区间![]() 上的图象。
上的图象。
18. (本小题满分12分)某小组中有男生、女生若干人,如果从中选一从参加某项测试,女生被选中的概率是![]() ;如果从中选两人参加测试,两人都是女生的概率为
;如果从中选两人参加测试,两人都是女生的概率为![]() (每个人被选中是等可能的).
(每个人被选中是等可能的).
(Ⅰ)求该小组男生、女生各多少人?
(Ⅱ)从该小组中选出3人,求男、女生都有的概率;
(Ⅲ)若对该小组的同学进行某项测试,其中女生通过的概率为![]() ,男生通过的概率为
,男生通过的概率为![]() ,现对该小组中男生甲、乙和女生丙三人进行测试,求恰有两人通过测试的概率。
,现对该小组中男生甲、乙和女生丙三人进行测试,求恰有两人通过测试的概率。
19 .(本小题满分12分)解关于![]() 的不等式
的不等式![]() 。
。
20.(本小题满分12分)已知圆C:![]()
![]() 经过点
经过点![]() 及点
及点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,直线
,直线![]() 与圆C相切。
与圆C相切。
(1)求实数![]() ;
;
(2)若实数![]() 满足约束条件
满足约束条件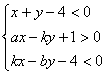 ,且使目标函数
,且使目标函数![]() 取最小值的最优解有无穷多个,求实数
取最小值的最优解有无穷多个,求实数![]() 的值。
的值。
21、(本小题满分12分)
已知函数![]() ,
, ![]() 为其图像上任意一点,过点
为其图像上任意一点,过点![]() 的切线的斜率
的切线的斜率![]() ,且函数
,且函数![]() 有极小值1,
有极小值1,
(1)求函数![]() 的表达式及其函数
的表达式及其函数![]() 的极大值.
的极大值.
(2)当-2≤x≤4时,讨论方程f(x)=m的解的个数
22.(本小题14分)已知![]() ,满足
,满足![]() 。
。
(Ⅰ)求数列![]() 的通项公式,并指出数列为何数列:
的通项公式,并指出数列为何数列:
(Ⅱ)![]() (n>2,
(n>2,![]() )
)
南昌一中高三第三次月考数学试题(文科)参考答案
一.选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | D | B | A | C | B | C | C | B | D | D |
二.填空题:(13)![]() 14。
14。![]() 、(14)
、(14)![]() 、(16)7
19 0 50 71 7
、(16)7
19 0 50 71 7
512 3 58
三.解答题:
17解:(Ⅰ)
![]()
![]()
![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]()
(Ⅱ)图象(略)
18解:(Ⅰ)女生6人,男生4人;
(Ⅱ)![]() ;
;
(Ⅲ)恰有两人通过的概率是:![]()
19解:原不等式等价于:![]() ,
,
(1)
当![]() 时,解集为
时,解集为![]() ;
;
(2)
当![]() 时,不等式等价于
时,不等式等价于![]() ,
,
①![]() 时,解集为
时,解集为![]() ;
;
②![]() 时,解集为
时,解集为![]() 。
。
20解:(1)由条件得到,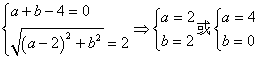 (舍去),
(舍去),
 又因为相切得到:
又因为相切得到: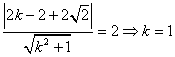 ;
;
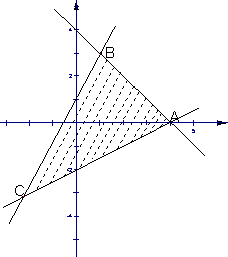
(2)约束条件是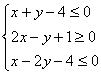 ,得到如图可行域:
,得到如图可行域:
由目标函数![]() 中
中![]() 的几何意义是直线
的几何意义是直线![]() 在
在![]() 轴上的截距,知道当这条直线平行图中BC时,满足条件,所以
轴上的截距,知道当这条直线平行图中BC时,满足条件,所以
![]() 。
。
21![]()
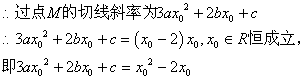
![]()

(2)由(1)知f(x)在![]()
![]() 是增函数,(0,2)上是减函数,
是增函数,(0,2)上是减函数,
易得m=1或![]() 时两个根;m
时两个根;m![]() 三个根;
三个根;![]() 或
或![]() 一个解,其他无解
一个解,其他无解
22解:(Ⅰ)由![]() 得:
得:![]() (1分)
(1分)
![]() 所以,
所以,![]() ,数列是等差数列.
4分
,数列是等差数列.
4分
(Ⅱ) ![]()
![]() ①
①
![]() ②
②
①-②,得 ![]()
=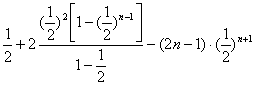
=![]()
∴ ![]() 8分
8分
令![]() 当
当![]()
∵![]()
![]() =
=![]()
=![]() ∵n>2 ∴
∵n>2 ∴ ![]() ∴
∴ ![]()
∴g(n)是关于![]() 的递增数列,即
的递增数列,即![]() ,而
,而![]() ∴
∴
![]() 12分
12分