高三第四次段考数学科（理科）试题
本试卷分选择题和非选择题两部分，满分150分.考试时间120分钟.
注意事项：
1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用像皮擦干净后，再选涂其它答案，不能答在试题卷上.
3．考试结束，监考人将答题卡收回.
第一部分 选择题（共40分）
一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的
１．若
,则下列结论不正确的是( )
Ａ．
Ｂ．
Ｃ．
Ｄ．
2．在各项都为正数的等比数列
中,首项是
,前三项和为21,则
( )
Ａ．33 Ｂ．72 Ｃ．84 Ｄ．189
３．设函数
(其中
),若函数
图象的一条对称轴为
，那么
（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
4．已知直线
,平面
,给出下列命题中正确的是(
)
(1) 若
,则
;
(2) 若
,则
;
(3) 若
,则;
(4) 若异面直线
互相垂直,则存在过
的平面与
垂直．
Ａ．（２）（３） Ｂ．（１）（３） Ｃ．（２）（４） Ｄ．（３）（４）
5．若奇函数
，当
时，
，则不等式
的解集是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ． 
6．实数
满足
,则
的最大值是( )
Ａ．
Ｂ．7 Ｃ．5 Ｄ．８
7．如果直线
与直线
关于直线
对称,那么( )
Ａ．
Ｂ．
Ｃ．
Ｄ．
8．已知圆锥的底面半径为
，高为
，在它的所有内接圆柱中，全面积的最大值的是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
第二部分 非选择题（共110分）
二、填空题：本大题共6小题，每题5分，共30分.
９．由抛物线
和直线
所围成图形的面积为________________．
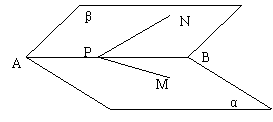10．如图,已知Ｐ是二面角
棱上的一点，
分别在
平面上引射线
，如果
，
．
那么的大小为
．
11．甲、乙两人同时从学校去县城开会，已知甲以速度
走了一半时间，另一半时间的速度是
，乙用速度走了一半路程，另一半路程的速度是，
，则甲、乙两人先到达县城的是
．
12．将抛物线
的图象按
平移后，抛物线与直线
相切，则
．
13．定义运算
，例如，
，则函数
的最大值
为
．
14．数列
是正项等差数列，若
，则数列
也为等差数列. 类比上述结论，写出正项等比数列
，若
=
，则数列{}也为等比数列.
三解答题：本大题共6小题，共80分，解答应写出文字说明、证明过程或演算步骤.
15．（本小题12分） 在△ABC中，角A、B、C的所对边分别为a、b、c，已知
，且最长边边长为1.求：（１）角C的大小；（２）△ABC最短边的长．
16．（本小题12分）设函数
，其中
，求的单调区间．
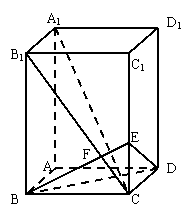
17．（本小题14分）已知长方体
中，
棱
棱
，连结
，
过
点作的垂线交
于
，交于
．
（1）求证：
平面
；
（2）求点
到平面
的距离；
（3）求平面与直线
所成角的正弦值．
18．（本小题14分）设
，令
，
，又
，
．
（１）判断数列
是等差数列还是等比数列并证明；
（２）求数列的通项公式；
（３）求数列
的前项和．
19．（本小题14分）已知平面上一定点
和一定直线
Ｐ为该平面上一动点，作
垂足为
，
．
(1) 问点Ｐ在什么曲线上？并求出该曲线方程；
(2)
点Ｏ是坐标原点，
两点在点Ｐ的轨迹上，若
求
的取值范围．
20．（本小题14分）设关于
的一元二次方程
的两个根为
，函数
．
(1) 求
的值；
(2) 证明是
上的增函数；
(3) 当为何值时，在区间上的最大值与最小值之差最小？