高三第一次教学质量检测题数学（理科）试题
第I卷（选择题，共50分）
一、选择题
1、复数
（ ）
A -1 , B 1 , C -32 , D 32
2、函数y=cos
的一条对称轴方程是（ ）
3、若{
}是等差数列，则下列结论不正确的是（ ）
A 其
奇数项
是成等差数列；
B 各项的平方
成等差数列；
C 各项减去一个常数所得的差-K（K是常数）成等差数列；
D 各项的K倍K（K是常数）成等差数列；
4、已知集合A={xx-3<5}，B={xx<a}，且A
B，则a的取值范围是（ ）
A a ≥5 ; B a>-5 ; C a>8 ; D a≥8
5、从80名女生和40名男生中选出6名学生组成课外学习小组，如果按性别比例分层抽样，则不同的抽取方法和数是( )
6、如果x,y是实数，那么xy>0是x+y=x+y的（ ）
A 充分不必要的条件 ； B 必要不充分的条件 ；
C 充要条件 ； D 不充分也不必要的条件。
7、已知
是双曲线
的两焦点，以线段
为边作正三角形M，若M
的中点在双曲线上，则双曲线的离心率是( )
8、如图所示，函数
的反函数的图象大致是（ ）
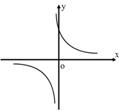
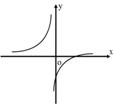
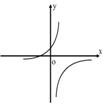
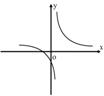
A B C D
9、若直线
的周长，则
的取值范围是（ ）
10、若函数
在其定义域的一个子区间
上不是单调函数，则实数
的取值范围是（ ）
第II卷（非选择题，共100分）
二、填空题
11、若椭圆
的一条准线经过抛物线
的焦点，若椭圆的左右焦点分别是，P为椭圆上的任一点，则三角形P的面积的最大值为_______.
12、设各项均为实数的等比数列{}的前n项的和
，若
，
，则
。
13、设
为偶函数，当
时，都有
14、⊿ABC的外接圆半径R=
，且满足
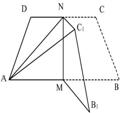
15、如图，在梯形ABCD中，M、N分别是AB，CD的中点，AB=2CD=4MN，将四边形MNCB沿MN将MNCB折成MN
，使二面角A—MN—
是直二面角，对于下列四个等式：
（1）
，（2）
（3）
，（4）
，则其中成立的序号为______________.
三、 解答题（本大题共6个小题，计80分）
16、（12分）已知锐角⊿ABC中，三内角A、B、C，两向量
若
与
共线，
（1）
求角A的大小；（2）求函数
取最大值时，角B的值。
17、（12分）某车间在三天内，每天生产10件某产品，其中第一、二天分别生产出了1、2件次品，而质检部门每天要在生产的10件产品中随机地抽取4件进行检查，若发现有次品，则当天的产品不能通过。
（1） 求第一天通过的概率；（2）求前两天全部通过检查的概率；
（3）若厂内对车间生产的新产品采用记分制，两天全不通过记零分，通过一天、二天分别记1、2分，求该车间在这两天得分的数学期望。
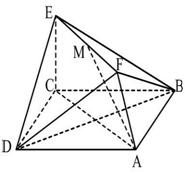18、（14分）如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AF=1，AB=
，M是线段EF的中点。
（1）求证：MN//平面BDE； （2）求二面角A—DF—B的大小；
（3）试在线段AC上确定一点P，使得PF与CD所成的角是600
19、（14分）已知点
都在直线：y=2x+2上，
为直线l与x轴的交点，数列{}是等差数列，公差为1。
（1） 求数列{}与{
}的通项公式；
（2）
若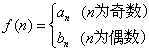
, 问是否存在
，若存在，求出k的值，若不存在，说明理由？
（3） 求证：
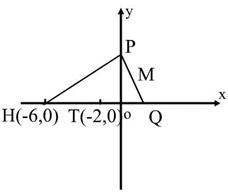
20、（14分）已知点H（-6，0），点P在Y轴的正半轴上，点Q在X轴的正半轴上，点M在直线PQ上，且满足
。
（1） 当点P在Y轴的正半轴上，点Q在X轴的正半轴上运动时，求点M的轨迹C的方程。
（2）若过点T（-2，0）作直线l与轨迹C交于A、B两点，则在X轴上是否存在一点E（m，0），使得⊿ABE为正三角形？若存在，求出直线l的方程；若不存在，说明理由？
21、（14分）已知函数
（Ⅰ）求函数在[1，e]上的最大、最小值；
（Ⅱ）求证：在区间
（III）求证：