高三第一次月考数学(文)试题
一.选择题![]()
1.等差数列![]() 中,已知
中,已知![]()
![]() ,
,![]() ,则
,则![]() 为( )
为( )
A.50 B.51 C.52 D.53
2.设![]() ,
,![]() ,
,![]() 的值等于( )
的值等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.平面内与定点![]() 和定直线
和定直线![]() 的距离相等的点的轨迹是
的距离相等的点的轨迹是
A.抛物线 B.椭圆 C.双曲线 D.直线
4.已知函数![]() (
(![]() 为自然对数的底),下列判断中正确的是( )
为自然对数的底),下列判断中正确的是( )
A.函数![]() 无零点;
无零点;
B.函数![]() 有且只有一个零点,且该零点在区间
有且只有一个零点,且该零点在区间![]() 内;
内;
C.函数![]() 有两个零点,其中一个为正数,另一个为负数;
有两个零点,其中一个为正数,另一个为负数;
D.函数![]() 有且只有一个零点,且该零点在区间
有且只有一个零点,且该零点在区间![]() 内。
内。
5.在长为![]() 的线段
的线段![]() 上任取一点
上任取一点![]() ,以
,以![]() 为底边构造等腰直角三角形
为底边构造等腰直角三角形![]() ,则这个等腰直角三角形的面积介于
,则这个等腰直角三角形的面积介于![]() 与
与![]() 之间的概率是( )
之间的概率是( )
A.0.1 B.0.3 C.0.5 D.0.8
6.设椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,以
,以![]() 为圆心,
为圆心,![]() (
(![]() 为椭圆中心)为半径作圆
为椭圆中心)为半径作圆![]() ,若它与椭圆的一个交点为
,若它与椭圆的一个交点为![]() ,且
,且![]() 恰好为圆
恰好为圆![]() 的一条切线,则椭圆的离心率为( )
的一条切线,则椭圆的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设函数![]() 是奇函数,
是奇函数,![]() ,
,![]() ,则
,则![]()
A.0 B.1 C.![]() D.5
D.5
8.设函数![]() ,若对任意
,若对任意![]() 都有
都有![]() 成立,则
成立,则![]() 的最小值为( )
的最小值为( )
![]() .4
.4 ![]() .2
.2
![]() .1
.1
![]() .
.![]()
9.设![]() 的最小值是
的最小值是
A.![]() B.
B.![]() C.-3 D.
C.-3 D.![]()
10.设四面体ABCD各棱长均相等,E,F分别为AC,AD中点,则![]() 在该四面体的面ADC的射影是
在该四面体的面ADC的射影是
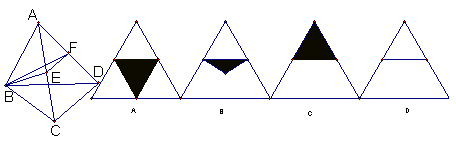 |
二.填空题![]()
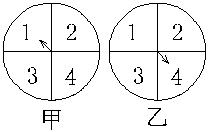 11.同时转动如下图所示的两个转盘,记转盘(甲)得到的数字为
11.同时转动如下图所示的两个转盘,记转盘(甲)得到的数字为![]() ,转盘(乙)得到的数字为
,转盘(乙)得到的数字为![]() ,则事件
,则事件![]() 的概率为
;
的概率为
;
 12.已知函数
12.已知函数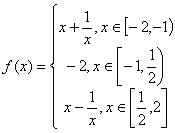 ,则
,则![]() 的值域为
的值域为
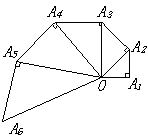
13.如图,![]() ,直角三角形
,直角三角形![]()
的直角边![]() ,记
,记![]()
![]() ,则
,则
数列![]() 的通项公式为
;
的通项公式为
;
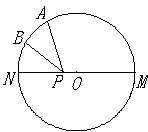 14.(2选1) (1)通过坐标伸缩变换T,由曲线
14.(2选1) (1)通过坐标伸缩变换T,由曲线![]() 得到曲线
得到曲线![]() ,这个坐标伸缩变换是
,这个坐标伸缩变换是
(2).如图,点A是半圆上一个三等分点,点B是弧AN的
中点,点P是直径MN上一个动点,圆![]() 的半径为1,则
的半径为1,则
![]() 的最小值为
;
的最小值为
;
姓名 学号 分数
一.选择题![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二.填空题![]()
11. ;12. ;
13.
14.⑴ ⑵.
三.解答题(共3题,共30分)
15.如图为一个观览车示意图.该观览车圆半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈.途中![]() 与地面垂直.以
与地面垂直.以![]() 为始边,逆时针转动
为始边,逆时针转动![]() 角到
角到![]() .设
.设![]() 点与地面距离为
点与地面距离为![]() .(1)求
.(1)求![]() 与
与![]() 的函数解析式;(2)设从
的函数解析式;(2)设从![]() 开始转动,经过80秒到达
开始转动,经过80秒到达![]() ,求
,求![]() .
.
16.已知平面内三点![]() 、
、![]() 、
、![]() 三点在一条直线上,
三点在一条直线上,![]() ,
,![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() ,
,![]() 的值.
的值.
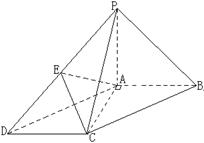 17 如图,在底边为平形四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
17 如图,在底边为平形四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(1)求证:AC⊥PB;(2)求证:PB∥平面AEC;
18.如图,在直角坐标系![]() 中,设椭圆
中,设椭圆![]() 的左右两个焦点分别为
的左右两个焦点分别为![]() .过右焦点
.过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
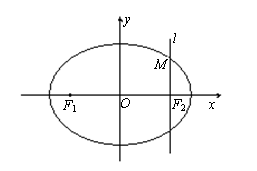 (2)设椭圆
(2)设椭圆![]() 的一个顶点为
的一个顶点为![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,求△
,求△![]() 的面积.
的面积.
19.已知数列![]() 的前n项和为Sn,且对一切正整数n都有
的前n项和为Sn,且对一切正整数n都有![]()
(Ⅰ)求证:![]()
(Ⅱ)求数列![]() 的通项公式.
的通项公式.
20已知点P在曲线![]() 上,曲线C在点P处的切线与函数
上,曲线C在点P处的切线与函数![]() 的图象交于点A,与
的图象交于点A,与![]() 轴交于点B,设点P的横坐标为
轴交于点B,设点P的横坐标为![]() ,点A,B的横坐标分别为
,点A,B的横坐标分别为![]() ,记
,记![]()
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,当![]() 时,证明不等式
时,证明不等式![]() .
.
高三第一次月考数学(文)试题
数学(文)答案
一.选择题
1.D;2.A;3.A;4.B.![]() ;5.B,
;5.B,![]() ;6.A,
;6.A,![]() ;7.C,解法1:取
;7.C,解法1:取![]() ;解法2:
;解法2:![]() ;8.B, 由
;8.B, 由![]() ,
,![]() 是最小值,
是最小值, ![]() 是最大值,
是最大值, ![]() 的最小值为
的最小值为![]() ;9.C,解法1:
;9.C,解法1:![]() , 解法2:均值不等式, 解法3:数形结合法.10.B
, 解法2:均值不等式, 解法3:数形结合法.10.B
二.填空题
11.![]() ;12.
;12.![]() ;13.
;13.![]() ,
,![]() ;14(1)
;14(1) 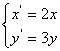 (2)
(2)![]()
15.解 (1)
∵![]() ,
,
∴![]()
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,![]() (m)
(m)
16.由于O、A、B三点在一条直线上,则![]() ∥
∥![]() ,而
,而![]() ,
,
![]() ∴
∴![]() ,又
,又![]() ,∴
,∴![]()
联立方程组解得![]() 或
或![]() .
.
17. (1)证明:∵PA⊥平面ABCD AB⊥AC ∴AC⊥PB
(2)证明:连结BD交AC于O,连结EO
∵平行四边形ABCD∴O为BD中点
又∵E为PD中点∴EO∥PB
又∵PB不在平面AEC中,EO在平面AEC中
∴PB∥平面AEC
18. (1) 解法一:
![]() 轴,∴
轴,∴![]() 的坐标为
的坐标为![]() .
.
由题意可知 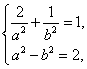 得
得 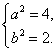 ∴所求椭圆方程为
∴所求椭圆方程为![]() .
.
解法二:
由椭圆定义可知![]() .由题意
.由题意![]() ,∴
,∴![]() .
.
又由![]() △
△![]() 可知
可知![]() ,
,![]() ,∴
,∴![]() ,
,
又![]() ,得
,得![]() .∴椭圆
.∴椭圆![]() 的方程为
的方程为![]() .
.
(2) 直线![]() 的方程为
的方程为![]() .
.
由 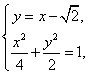 得点
得点![]() 的纵坐标为
的纵坐标为![]() .
.
又![]() ,∴
,∴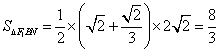 .
.
19.(Ⅰ)证明:![]() ①
①
![]() ②
②
由②—①得 ![]()
![]()
![]() ③
③
(Ⅱ)解法一:由(Ⅰ)知![]() ④
④
④—③,得![]() 从而
从而![]()
故![]() 均为公差为4的等差数列.
均为公差为4的等差数列.
在①中令![]()
![]() 在③中令
在③中令![]()
![]()
综上知,![]()
解法二:由③式知,![]()
记![]() 在①中令
在①中令![]() 得,
得,![]()
![]()
![]() 即
即![]()
20解:(Ⅰ)![]() 的导数
的导数![]() ,又
,又![]() 点P的坐标为
点P的坐标为![]() ,
,![]() 曲线C在P点的切线的斜率为
曲线C在P点的切线的斜率为![]() ,
,
则该切线方程为![]() ,令
,令![]() ,得
,得![]()
由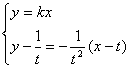 ,得
,得![]() ,
,![]()
因此,![]() 的解析式为:
的解析式为:![]()
(2)![]() 时,
时,![]() ,
,![]() ,即
,即![]()
①当![]() 时,
时,![]() ,
,![]() 数列
数列![]() 是以0为首项的常数数列,则
是以0为首项的常数数列,则![]()
②当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
![]() ,解得
,解得![]()
综合①、②得![]() (Ⅲ)
(Ⅲ)![]() ,
,![]() ,
,![]()
![]() ,
,![]() 则
则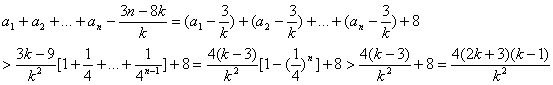
![]() ,
,![]()
因此,不等式![]() 成立
成立