高级中学高三数学周练(8)
1.已知向量![]() ,
,![]() ,则向量
,则向量![]() 与
与![]()
A.互相平行
B.互相垂直
C.夹角为![]() D.夹角为
D.夹角为![]()
2.已知![]() ,
,![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知![]() ,
,![]() ,当
,当![]() 时,代数式
时,代数式![]() 的值是
的值是
A.正数 B.负数 C.![]() D.介于
D.介于![]() 与
与![]() 之间
之间
4.“神六飞天,举国欢庆”,据科学计算,运载“神州”六号飞船的“长征”二号系列火箭在点火1分钟通过的路程为![]() ,以后每分钟通过的路程比前一分钟增加
,以后每分钟通过的路程比前一分钟增加![]() ,在达到离地面
,在达到离地面![]() 的高度时,火箭与飞船分离,则这一过程大约需要的时间是
的高度时,火箭与飞船分离,则这一过程大约需要的时间是
A.![]() 分钟
B.
分钟
B.![]() 分钟
C.
分钟
C.![]() 分钟
D.
分钟
D.![]() 分钟
分钟
5.条件![]() :“直线
:“直线![]() 在
在![]() 轴上的截距是在
轴上的截距是在![]() 轴上的截距的两倍”;条件
轴上的截距的两倍”;条件![]() :“直线
:“直线![]() 的斜率为
的斜率为![]() ”,则
”,则![]() 是
是![]() 的
的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.非充分也非必要条件
6.设函数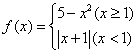 ,则不等式
,则不等式![]() 的解集为
的解集为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.若实数![]() 、
、![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知三个不等式:![]() (其中a,b,c,d均为实数),用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成的正确命题的个数是
(其中a,b,c,d均为实数),用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成的正确命题的个数是
A. 0 B. 1 C. 2 D. 3
9.图像![]() 与函数
与函数![]() 的图像关于
的图像关于
A.直线![]() 对称 B.点
对称 B.点![]() 对称 C.直线
对称 C.直线![]() 对称 D.点
对称 D.点![]() 对称
对称
10.直线![]() 与圆
与圆![]() 相切,并且在两坐标轴上的截距之和等于
相切,并且在两坐标轴上的截距之和等于![]() ,则直线
,则直线![]() 与两坐标轴围成的三角形的面积等于
与两坐标轴围成的三角形的面积等于
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
11.![]() 的三个内角分别为
的三个内角分别为![]() 、
、![]() 、
、![]() ,若
,若![]() 和
和![]() 是关于
是关于![]() 的方程
的方程![]() 的两实根,则
的两实根,则![]() .
.
12.在![]() 中,
中,![]() 为中线
为中线![]() 上一个动点,若
上一个动点,若![]() ,则
,则![]() 的最小值是
.
的最小值是
.
13.已知实数![]() 、
、![]() 满足约束条件
满足约束条件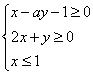
![]() ,目标函数
,目标函数![]() 只有当
只有当![]() 时取得最大值,则
时取得最大值,则![]() 的取值范围是
.
的取值范围是
.
14.要得到![]() 的图像,且使平移的距离最短,则需将
的图像,且使平移的距离最短,则需将![]() 的图像
的图像
即可得到.
15.已知正数x、y满足x+2y=1,则![]() 的最小值是
.
的最小值是
.
16.已知函数![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() 的取值范围为 .
的取值范围为 .
17.在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边是
所对的边是![]() 、
、![]() 、
、![]() ,且
,且![]() .(1)求
.(1)求![]() 值 ;(2)若
值 ;(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
18.已知函数![]() 满足
满足![]()
(1)求函数![]() 解析式及定义域; (2)求函数
解析式及定义域; (2)求函数![]() 的反函数
的反函数![]() ; (3)若
; (3)若![]() ,求x的取值范围.
,求x的取值范围.
19.(本小题共14分)已知两点![]() ,且动点
,且动点![]() 使
使![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求点![]() 的轨迹
的轨迹![]() ;
;
(2)设![]() 、
、![]() 分别是直线
分别是直线![]() 与
与![]() 上的两点,且
上的两点,且![]() 是直线
是直线![]() 的方向向量,直线
的方向向量,直线![]() 与曲线
与曲线![]() 相切,当
相切,当![]() 是以
是以![]() 为底边的等腰三角形时,求
为底边的等腰三角形时,求![]() 的值.
的值.
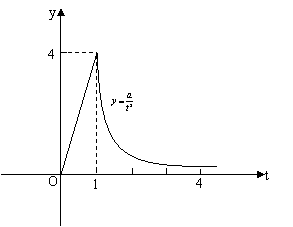
20.(本小题共14分)某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间近似满足如图所示的曲线.
(小时)之间近似满足如图所示的曲线.
(1)写出第一次服药后![]() 与
与![]() 之间的函数关系式
之间的函数关系式![]() ;
;
(2)据进一步测定:每毫升血液中含药量不少于![]() 微克时,治疗有效.
微克时,治疗有效.
①求服药一次后治疗有效的时间是多长?
 ②当
②当![]() 时,第二次服药,问
时,第二次服药,问![]() 时药效能否持续?
时药效能否持续?
21.设Sn是数列![]() 的前n项和,且
的前n项和,且![]() .
.
(1)求数列![]() 的通项公式;(2)设数列
的通项公式;(2)设数列![]() 使
使![]()
![]() ,求
,求![]() 的通项公式;
的通项公式;
(3)设![]() ,且数列
,且数列![]() 的前n项和为Tn,试比较Tn与
的前n项和为Tn,试比较Tn与![]() 的大小.
的大小.
高三数学周练(8)答案
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.B 2. C 3.B 4. C 5. B 6. C 7. D 8.C
9.B 10. A
第Ⅱ卷
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.
11.![]() 12.
12.![]() 13.
13.![]() 14.向左平移
14.向左平移![]() 单位
单位
15.
![]() 16.
16.![]()
三、解答题:本大题共5小题,共70分。解答应写出文字说明,证明过程或演算步骤.
17.(本小题共12分)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边是
所对的边是![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
(1)求![]() 值 ;
值 ;
(2)若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
(1)![]()
![]() ,
,![]() ,
, ![]() 2分
2分
由![]() ,
,
![]()
![]() ;
;![]() 6分
6分
(2)![]()
![]() ,且
,且![]() ,
,![]()
![]() ,
,
又![]() ,
,![]() ,
,
![]() 9分
9分
![]() .
.
![]() 11分
11分
当切仅当![]() 时,
时,![]() 面积取最大值,最大值为
面积取最大值,最大值为![]() .
. ![]() 12分
12分
18. (1)设t=x-3,则x=t+3.
∵ ![]() ∴
∴![]() …………1分
…………1分
∵ ![]() ,∴
,∴![]() 由
由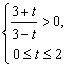 得
得![]() …………2分
…………2分
于是![]() 且定义域为[0,2].
…………1分
且定义域为[0,2].
…………1分
(2)设y=![]() 则
则![]() ,即
,即![]() ,
,
∴![]()
![]() .
…………2分
.
…………2分
∵![]() ∴
∴![]() ,∴
,∴ ![]()
从而![]() .
.
故函数![]() 的反函数为
的反函数为![]()
![]() (
(![]() ).
…………2分
).
…………2分
(3)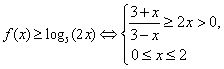
![]()
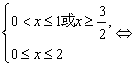
![]()
19.(本小题共14分)已知两点![]() ,且动点
,且动点![]() 使
使![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求点![]() 的轨迹
的轨迹![]() ;
;
(2)设![]() 、
、![]() 分别是直线
分别是直线![]() 与
与![]() 上的两点,且
上的两点,且![]() 是直线
是直线![]() 的方向向量,直线
的方向向量,直线![]() 与曲线
与曲线![]() 相切,当
相切,当![]() 是以
是以![]() 为底边的等腰三角形时,求
为底边的等腰三角形时,求![]() 的值.
的值.
(1)设![]() ,由
,由![]() ,得
,得
![]() ,
,![]()
![]() ,
,![]() 3分
3分
于是,![]() ,
,![]() ,
,![]() 成等差数列等价于
成等差数列等价于
![]()
![]()
![]()
![]() 6分
6分
所以点![]() 的轨迹是以原点为圆心,
的轨迹是以原点为圆心,![]() 为半径的圆;
为半径的圆;
![]() 7分
7分
(2)设直线![]() 的方程为
的方程为![]() ,
,![]() 、
、![]() ,
,
![]() 直线
直线![]() 与曲线
与曲线![]() 相切,
相切,![]()
![]() ,即
,即![]()
![]() ①,
①, ![]() 9分
9分
由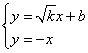
![]()
![]() ,同理
,同理![]() ,
,
![]() 的中点
的中点![]() ,
,
![]() 10分
10分
![]()
![]() 是以
是以![]() 为底边的等腰三角形,
为底边的等腰三角形,
![]() ,即
,即![]()
![]() ②,
②,
![]() 12分
12分
由①②解得![]() .
.
![]() 14分
14分
20.(本小题共14分)某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间近似满足如图所示的曲线.
(小时)之间近似满足如图所示的曲线.
(1)写出第一次服药后![]() 与
与![]() 之间的函数关系式
之间的函数关系式![]() ;
;
(2)据进一步测定:每毫升血液中含药量不少于![]() 微克时,治疗有效.
微克时,治疗有效.
①求服药一次后治疗有效的时间是多长?
②当![]() 时,第二次服药,问
时,第二次服药,问![]() 时药效能否持续?
时药效能否持续?
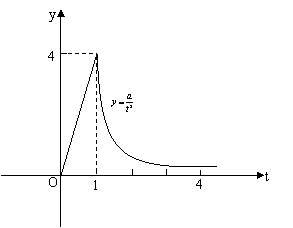
⑴当 ![]() 时,
时,![]() ,
,
此时![]() 在曲线上,所以
在曲线上,所以![]() ,
,
![]() 2分
2分
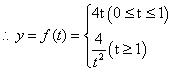
![]() 4分
4分
⑵①因为 ,
, ![]() 7分
7分
所以服药一次治疗疾病的有效时间为![]()
![]() 8分
8分
②设![]() ,
,![]() 小时第二次服药后,血液中含药量
小时第二次服药后,血液中含药量![]() 为第二次产生的含药量
为第二次产生的含药量![]() 微克以及第一次的剩余量
微克以及第一次的剩余量![]() ,
, ![]() 11分
11分
只要说明当![]() 时,
时,![]() 即可说明药效持续,否则不持续。
即可说明药效持续,否则不持续。
利用单调性的定义可证明![]() 在
在![]() 上是增函数。
上是增函数。![]() 13分
13分
故![]() ,因此当
,因此当![]() 时第二次服药,
时第二次服药, ![]() 药效持续.
药效持续. ![]() 14分
14分
21. ∵![]() ,∴
,∴![]() ,
,
于是an+1=Sn+1-Sn=(2 an+1-2)-(2 an-2),即an+1=2an. …………2分
又a1=S1=2 a1-2, 得a1=2. …………1分
∴![]() 是首项和公比都是2的等比数列,故an=2n.
…………1分
是首项和公比都是2的等比数列,故an=2n.
…………1分
(2) 由a1b1=(2×1-1)×21+1+2=6及a1=2得b1=3. …………1分
当![]() 时,
时,![]()
![]() ,
,
∴![]() .
…………2分
.
…………2分
∵an=2n,∴bn=2n+1(![]() ).
).
∴![]()
(3)![]() .
.
![]() .
.